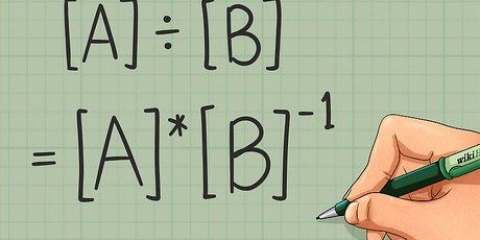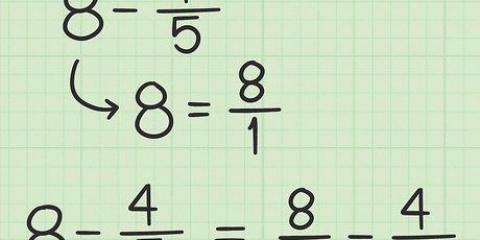Transponer una matriz: 11 pasos (con fotos)

Contenido

Pasos
Consejos

Una transposición de matrices es una herramienta matemática útil para comprender la estructura de las matrices. Las características que quizás ya conozca de las matrices, como ser cuadradas y simétricas, afectan los resultados de la transposición de manera obvia. La transposición también sirve para expresar vectores como matrices, o calcular los productos de vectores. Cuando se trata de matrices complejas, el concepto estrechamente relacionado de una transposición conjugada lo ayudará con muchos problemas.

Pasos

Parte 1 de 3: Transponer una matriz

Imagen titulada Transponer una matriz Paso 1

1. Comience con cualquier matriz. Puede transponer cualquier matriz independientemente del número de filas y columnas. Las matrices cuadradas, con el mismo número de filas y columnas, son las que más se transponen, por lo que usaremos una matriz cuadrada simple como ejemplo:

matriz a =
1 2 3
4 5 6
7 8 9

Imagen titulada Transponer una matriz Paso 2

2. Hacer que la primera fila de la matriz sea la primera columna de la transposición. Reescriba la fila uno de la matriz como una columna:

Transposición de matriz A = A

Primera columna de A:
1
2
3

Imagen titulada Transponer una matriz Paso 3

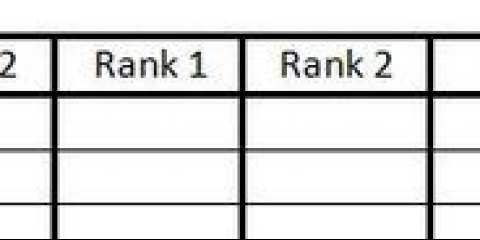
3. Repita para las filas restantes. La segunda fila de la matriz original se convierte en la segunda columna de la transposición. Repite este patrón hasta que hayas convertido cada fila en una columna:

a =
1 4 7
2 5 8
3 6 9

Imagen titulada Transponer una matriz Paso 4

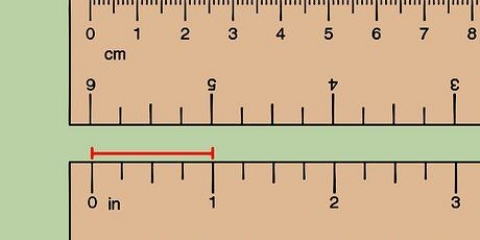
4. Practica en una matriz no cuadrada. La transposición es exactamente la misma para una matriz no cuadrada. Reescribe la primera fila como la primera columna, la segunda fila como la segunda columna, y así sucesivamente. Aquí hay un ejemplo codificado por colores para mostrarle dónde terminan los elementos:

matriz z =
4 7 2 1
3 9 8 6

matriz z =
4 3
7 9
2 8
1 6

Imagen titulada Transponer una matriz Paso 5

5. Expresar la transposición matemáticamente. El concepto es bastante simple, pero es bueno poder describirlo en términos matemáticos. No se necesita jerga fuera de la notación matricial básica:

Si la matriz B es una metro X norte matriz (m filas y n columnas), entonces la matriz B transpuesta es una norte X metro matriz (n filas y m columnas).

Para cada elemento b_xy (X-el, y-la columna) en B, la matriz B tiene un elemento igual en b_yx (y-La fila, X-la columna).

Parte 2 de 3: Casos especiales

Imagen titulada Transponer una matriz Paso 6

1. (M = M. La transposición de una transposición es la matriz original. Esto tiene mucho sentido, ya que solo estás intercambiando filas y columnas. Cambiarlos de nuevo te llevará de vuelta al principio.

Imagen titulada Transponer una matriz Paso 7

2. Inclinar matrices cuadradas sobre la diagonal principal. En una matriz cuadrada, una transposición `inclinará` la matriz a lo largo de la diagonal principal. En otras palabras, los elementos en una línea diagonal del elemento a₁₁ a la esquina inferior derecha siguen siendo los mismos. Los otros elementos se moverán a través de la diagonal y terminarán a la misma distancia de la diagonal, en el lado opuesto.

Si no puede visualizar esto, dibuje una matriz de 4x4 en una hoja de papel. Ahora dobla sobre la diagonal principal. ¿Ves cómo los elementos un₁₄ y un₄₁ tocarnos? Intercambian lugares en la transposición, como cualquier otro par que se toca cuando se pliega.

Imagen titulada Transponer una matriz Paso 8

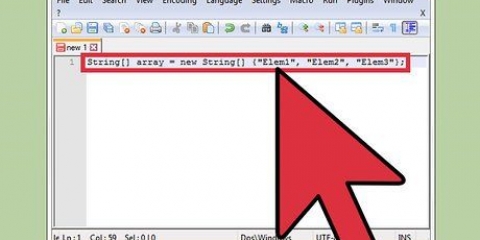
3. Transponer una matriz simétrica. Una matriz simétrica es simétrica respecto a la diagonal principal. Si usamos la `inclinación` o `doblar` como se describe arriba, podemos ver inmediatamente que nada cambia. Todos los pares de elementos que intercambian lugares ya eran idénticos. De hecho, esta es la forma estándar de definir una matriz simétrica. Si la matriz A = A, entonces la matriz A es simétrica.

Parte 3 de 3: transposición conjugada de una matriz compleja

Imagen titulada Transponer una matriz Paso 9

1. Empezar con una matriz compleja. Las matrices complejas tienen elementos con un componente real e imaginario. Si bien puede realizar una transposición regular de estas matrices, la mayoría de los cálculos prácticos son transposiciones conjugadas.

Matriz C =
2+I 3-2I
0+I 5+0I

Imagen titulada Transponer una matriz Paso 10

2. Tome la conjugación compleja. La conjugación compleja cambia el signo de las componentes imaginarias, sin cambiar las componentes reales. Realice esta operación para todos los elementos de la matriz.

Conjugación compleja de C =
2-I 3+2I
0-I 5-0I

Imagen titulada Transponer una matriz Paso 11

3. Transponer los resultados. Tome una conversión ordinaria del resultado. La matriz que obtienes es la transposición conjugada de la matriz original.

Transposición conjugada de C = C =
2-I 0-I
3+2I 5-0I

Consejos

Este artículo usa la notación A para denotar la conversión de la matriz A. La notación A` o Ã significa lo mismo.
Este artículo se refiere a la conversión conjugada de la matriz A como A, la notación más común en álgebra lineal. Los físicos cuánticos a menudo usan A en lugar. A* es otra opción, pero trate de evitar esto ya que algunas fuentes usarán este símbolo para indicar una conjugación compleja.