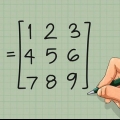Determinar el determinante de una matriz de 3x3: 12 pasos (con fotos)

Contenido

Pasos
- Parte 1 de 2: Determinar el determinante
- Parte 2 de 2: Simplificando el problema
Consejos

El determinante de una matriz es muy utilizado en matemáticas, álgebra lineal y geometría superior. Fuera del mundo científico, los ingenieros gráficos por computadora y los programadores usan con frecuencia los determinantes de las matrices. Lea este artículo para determinar el determinante de una matriz de 3x3.

Pasos

Parte 1 de 2: Determinar el determinante

Imagen titulada Encuentra el determinante de una matriz 3X3 Paso 1

1. Escriba su matriz de 3 x 3. Empezamos con una matriz A de 3 x 3 y probamos el determinante |A| gustar. Usamos la siguiente notación general para la matriz (y esta es nuestra matriz de ejemplo):

$metro = (\begin{matrix} a \end{matrix} 11 a_{12} a_{13} a_{21} & a_{22} & a_{23} a_{31} & a_{32} & a_{33}) = (\begin{matrix} 1 & 5 & 3 \\ 2 & 4 & 7 \\ 4 & 6 & 2 \end{matrix})$ $M={begin{pmatrix}a_{{11}}&a_{{12}}&a_{{13}}\a_{{21}}&a_{{22}}&a_{ {23}}\a_{{31}}&a_{{32}}&a_{{33}}end{pmatrix}}={begin{pmatrix}1&5&3\2& 4 y 7\4 y 6 y 2end{pmatrix}}$

Imagen titulada Encuentra el determinante de una matriz 3X3 Paso 2

2. Elija una fila o columna. Esta será su fila o columna de referencia. Obtendrás la misma respuesta sin importar cuál elijas. Ahora solo elige la primera fila. Más adelante le asesoraremos sobre cómo elegir la opción que le resulte más fácil de calcular.

Elijamos la primera fila de nuestra matriz de ejemplo A. Encierra en un círculo el 1 5 3. En términos generales, encierre en un círculo₁₁ a₁₂ a₁₃.

Imagen titulada Hallar el determinante de una matriz 3X3 Paso 3

3. Tacha la fila y la columna del primer elemento. Mire la fila o columna que marcó con un círculo y seleccione el primer elemento. Dibuja una línea a través de la fila y la columna correspondientes. Si todo va bien, esto ahora produce cuatro números. Tratamos esto como una matriz de 2 x 2.

En nuestro ejemplo, la fila de referencia es 1 5 3. Eso primer elemento está en la fila 1 y la columna 1. Tacha la fila 1 y la columna 1 por completo. Anote los elementos restantes como unmatriz 2x2:

~~1 5 3~~
2 4 7
4 6 2

Imagen titulada Hallar el determinante de una matriz 3X3 Paso 4

4. Determinar el determinante de la matriz 2 x 2. No lo olvides: la matriz

(\begin{matrix} a & B \\ C & D \end{matrix})

${begin{pmatrix}a&b\c&dend{pmatrix}}$ tiene un determinante de anuncio - ac. Lo sabes dibujando una cruz (X) a través de la matriz de 2 x 2. Multiplica los dos números conectados por el de la X. Luego resta el producto de los dos números conectados por el /. Usa esta fórmula para calcular el determinante de la matriz que acabas de encontrar.

En nuestro ejemplo, el determinante de la matriz es

(\begin{matrix} 4 & 7 \\ 6 & 2 \end{matrix})

${begin{pmatrix}4 y 7\6 y 2end{pmatrix}}$ = 4 * 2 - 7 * 6 = -34.

Este determinante se llama menor del elemento que elegimos en nuestra matriz original. En este caso tenemos el menor de a₁₁ Lo encontré.

Imagen titulada Encuentra el determinante de una matriz 3X3 Paso 5

5. Multiplique la respuesta por su elemento elegido. Recuerde que seleccionó un elemento de su fila (o columna) de referencia cuando decidió qué fila y columna tachar. Multiplique este elemento por el determinante que acaba de calcular para la matriz 2x2.

En nuestro ejemplo tenemos un₁₁ seleccionado, que tiene un valor de 1. Multiplique esto por -34 (el determinante de la matriz 2x2) para obtener 1*-34 = -34 Llegar.

Imagen titulada Encuentra el determinante de una matriz 3X3 Paso 6

6. Determina el signo de tu respuesta. Ahora multiplique la respuesta por 1 o por -1 para obtener el cofactor de tu elemento elegido. El que uses depende de la posición del elemento en la matriz 3x3. Memoriza la siguiente tabla simple para averiguar qué elemento causa qué:

+ - +
- + -
+ - +

Porque nosotros a₁₁ hemos elegido, marcados con un +, multiplicamos el número por +1 (es decir, no hacemos nada con él). la respuesta sigue siendo -34.

Otra forma de determinar el signo es con la fórmula (-1), donde I y j formar la fila y la columna del elemento.

Imagen titulada Encuentra el determinante de una matriz 3X3 Paso 7

7. Repita este proceso para el segundo elemento en su fila o columna de referencia. Continúe con la matriz original de 3x3, con la fila o columna que marcó anteriormente. Repite el mismo proceso con este elemento:

Cruza la fila y la columna de ese elemento. En este caso se selecciona el elemento a₁₂ (con valor 5). Cruce la primera fila (1 5 3) y la segunda columna

(\begin{matrix} 5 \\ 4 \\ 6 \end{matrix})

${begin{pmatrix}5\4\6end{pmatrix}}$ .

Tratar los elementos restantes como una matriz de 2x2. En nuestro ejemplo, la matriz es

(\begin{matrix} 2 & 7 \\ 4 & 2 \end{matrix})

${begin{pmatrix}2&7\4&2end{pmatrix}}$

Determine el determinante de esta matriz 2x2. Use la fórmula ad - bc. (2*2 - 7*4 = -24)

Multiplique esto por el elemento elegido de la matriz 3x3. -24 * 5 = -120

Determinar si multiplicar por -1. Usa la tabla de caracteres o la fórmula (-1). Tenemos el elemento a₁₂ elegido, y eso es un – en la tabla de personajes. Necesitamos cambiar el signo de nuestra respuesta: (-1)*(-120) = 120.

Imagen titulada Hallar el determinante de una matriz 3X3 Paso 8

8. Repita para el tercer elemento. Ahora tienes que encontrar un cofactor. Calcule i para el tercer término en su fila o columna de referencia. Aquí hay una explicación rápida de cómo calcular el cofactor de ₁₃ en nuestro ejemplo:

Cruce la fila 1 y la columna 3 y obtenga

(\begin{matrix} 2 & 4 \\ 4 & 6 \end{matrix})

${begin{pmatrix}2 y 4\4 y 6end{pmatrix}}$

Su determinante es 2*6 - 4*4 = -4.

Multiplique esto por el elemento a₁₃: -4 * 3 = -12.

elemento un₁₃ es un + en la tabla de caracteres, por lo que la respuesta es -12.

Imagen titulada Encuentra el determinante de una matriz 3X3 Paso 9

9. Sume los tres resultados juntos. Este es el paso final. Calculó cofactores, uno para cada elemento en una sola fila o columna. Súmalos y habrás encontrado el determinante de la matriz 3x3.

En nuestro ejemplo, el determinante es -34 + 120 + -12 = 74.

Parte 2 de 2: Simplificando el problema

Imagen titulada Encuentra el determinante de una matriz 3X3 Paso 10

1. Elija la referencia con más ceros. no olvides que tu cada puede elegir fila o columna como referencia. Obtendrás la misma respuesta sin importar lo que elijas. Si elige una fila o columna con ceros, solo necesita calcular el cofactor de los elementos que no son cero. La razon es la siguiente:

Suponga que elige la fila 2, con los elementos a₂₁, a₂₂, y un₂₃. Para resolver este problema nos fijamos en tres matrices diferentes de 2x2. Supongamos que llamamos a esto A₂₁, a₂₂ y un₂₃.
El determinante de la matriz 3x3 es un₂₁|Un₂₁| - a₂₂|Un₂₂| + un₂₃|Un₂₃|.
Si los términos a₂₂ y un₂₃ son ambos 0, entonces nuestra fórmula se convierte en₂₁|Un₂₁| - 0*|A₂₂| + 0*|A₂₃| = un₂₁|Un₂₁| - 0 + 0 = un₂₁|Un₂₁|. Ahora solo necesitamos calcular el cofactor de un solo elemento.

Imagen titulada Encuentra el determinante de una matriz 3X3 Paso 11

2. Sume las filas para simplificar la matriz. Si toma los valores de una fila y los agrega a otra fila, el determinante de la matriz no cambiará. Lo mismo ocurre con las columnas. Puede hacer esto repetidamente, o multiplicar los valores por una constante antes de sumar, para obtener tantos ceros en la matriz como sea posible. Esto te puede ahorrar mucho trabajo.

Por ejemplo, suponga que tiene una matriz de 3x3:

(\begin{matrix} 9 & - 1 & 2 \\ 3 & 1 & 0 \\ 7 & 5 & - 2 \end{matrix})

${begin{pmatrix}9&-1&2\3&1&0\7&5&-2end{pmatrix}}$

Cada 9 en posición a₁₁ para deshacernos de él, podemos multiplicar la segunda fila por -3 y agregar el resultado a la primera. La nueva primera fila se convierte en [9 -1 2] + [-9 -3 0] = [0 -4 2].

La nueva matriz es

(\begin{matrix} 0 & - 4 & 2 \\ 3 & 1 & 0 \\ 7 & 5 & - 2 \end{matrix})

${begin{pmatrix}0&-4&2\3&1&0\7&5&-2end{pmatrix}}$ Intenta usar el mismo truco para las columnas, para₁₂ hacer un 0.

Imagen titulada Encuentra el determinante de una matriz 3X3 Paso 12

3. Aprende el truco para resolver matrices triangulares. En estos casos especiales, el determinante es simplemente el producto de los elementos a lo largo de la diagonal principal, de un₁₁ arriba a la izquierda a un₃₃ abajo a la derecha. Seguimos hablando de matrices de 3x3, pero las matrices `triangulares` tienen patrones especiales de valores que no cero son:

Matriz de triángulo superior: todos los elementos distintos de cero están en o por encima de la diagonal principal. Todos los valores a continuación son cero.

Matriz de triángulo inferior: todos los elementos distintos de cero están sobre o debajo de la diagonal principal.

Matriz diagonal: todos los elementos distintos de cero están en la diagonal principal. (Un subconjunto de los anteriores.)

Consejos

Este método se puede utilizar para matrices cuadradas de cualquier tamaño. Por ejemplo, si usa esto para una matriz de 4x4, entonces mantiene después de la "tachar" una matriz de 3x3, para la cual puede calcular el determinante como se indica arriba. Ten cuidado, porque hacer esto a mano será muy aburrido!
Si todos los elementos de una fila o columna son iguales a 0, entonces el determinante de esa matriz es igual a 0.