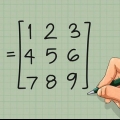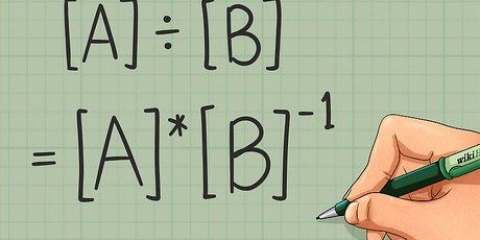Hallar la inversa de una matriz de 3x3: 6 pasos (con fotos)

Contenido

Pasos
Consejos
Advertencias

Calcular a mano la inversa de una matriz de 3x3 es una tarea tediosa. Pero también es útil y no es difícil, y ayuda a resolver varias ecuaciones matriciales.

Pasos

1. Determinar det(M), el determinante de la Matriz M. El determinante suele estar en el denominador de la inversa. Si el determinante es igual a cero, entonces la matriz no tiene inversa.

2. Determine M, la transposición de la matriz. Transponer significa reflejar la matriz en la diagonal principal o lo que sea lo mismo, intercambiando el elemento (i,j) y el elemento (j,i).

3. Determinar el determinante de cada una de las matrices menores de 2x2, las menores.

4. Muéstrelo como una matriz de cofactores como se muestra, y multiplique cada término por el signo indicado.El resultado de estos pasos es la matriz adjunta (a veces también matriz adjunta), escrita como Adj(M).

5. Encuentre la inversa dividiendo la matriz adyuvante encontrada en el paso anterior por el determinante del primer paso.

6. Estos pasos se pueden combinar transponiendo, copiando las dos primeras filas y columnas y determinando el determinante 2x2 alrededor de cada punto. Al verificar el trabajo, el determinante se calcula de tres maneras; si estos coinciden, entonces has encontrado la respuesta correcta. Con el "toro" método, el signo es inmediatamente correcto.

Consejos

Tenga en cuenta que el mismo método se puede aplicar a una matriz de variables e incógnitas, por ejemplo, una matriz algebraica, M, y su inversa, M.
Anota todos tus pasos porque es muy difícil resolver de memoria la inversa de una matriz de 3x3. Además, escribir te asegura que cometerás errores con menos rapidez.
Existen programas de computadora que calculan las inversas de una matriz por ti. , hasta un tamaño de matrices de 30x30

La matriz adyuvada es la transposición de la matriz de cofactores. Es por eso que transponemos la matriz en el paso 2, para encontrar una transposición de una matriz cofactor.
Comprueba si es correcto al multiplicar M por M. Ahora debería poder confirmar que M*M = M*M = I. I es la matriz de la unidad, que consta de unos a lo largo de la diagonal principal y ceros en todos los demás. Si no, cometiste un error en alguna parte.

Advertencias

No todas las matrices de 3x3 tienen inversa. Si el determinante de la matriz es 0, entonces no tiene inversa. (Tenga en cuenta que en la fórmula dividimos por det(M). La división por cero no es posible.)