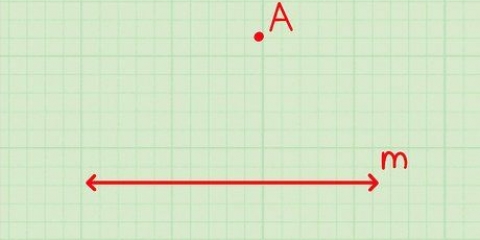
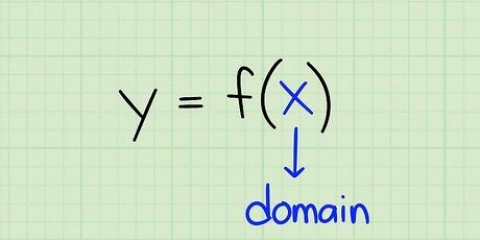
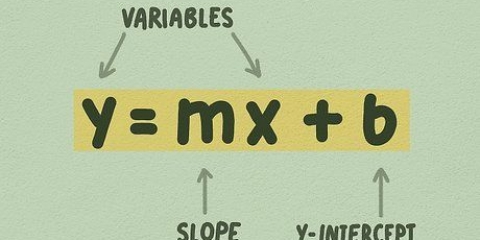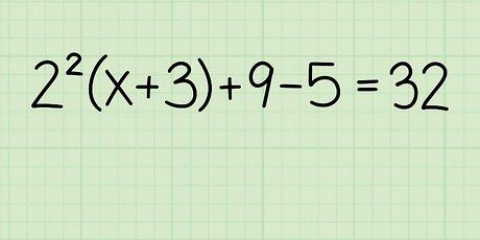Hay un punto y una pendiente dada. Se dan dos puntos, pero ninguna pendiente. Dado un punto y otra recta paralela a él. Dado un punto y otra recta perpendicular a él. 




Reordena tu ecuación. b = y - mx. Introduce los valores y resuelve. b = -5 - (2/3)6. b = -5 - 4. b = -9 Comprueba que la intersección con el eje y es realmente -9. Escribe la ecuación: y = 2/3 x - 9 

Usa tu pendiente y coordenadas en la ecuación anterior. Multiplica la pendiente (metro) con la coordenada x del punto. Resta el valor de la coordenada y del punto. ahora tienes B resuelta, la intersección con el eje y. 



Calcular la pendiente. La pendiente = (Y2 - Y1) / (X2 - X1) -12 - (-5) / 8 - 6 = -7 / 2 la pendiente es -7/2 (del primer punto al segundo vamos 7 hacia abajo y 2 hacia la derecha, por lo que la pendiente es -7 sobre 2). Reordena tu ecuación. b = y - mx. Introduce los valores y resuelve. b = -12 - (-7/2)8. b = -12 - (-28). b = -12 + 28. b = 16 Observación: como usamos el 8 para las coordenadas, también tenemos que usar el -12.Si usas el 6 para tus coordenadas, también debes usar el -5. Comprueba que tu intersección con el eje y es realmente 16. Escribe la ecuación: y = -7/2 x + 16 
Sustituye la pendiente y las coordenadas en la ecuación anterior. Multiplica la pendiente (metro) con la coordenada x del punto. Resta el valor de la coordenada y del punto. Tienes B resuelta, la intersección con el eje y. 


Resuelve la pendiente. La pendiente de nuestra nueva línea será la misma que la pendiente de la línea anterior. Determine la pendiente de la línea anterior: -2y = -5x + 1 jalar "-2" fuera de ambos lados: y = 5/2x - 1/2 la pendiente es 5/2. Reordena tu ecuación. b = y - mx. Completa y resuelve. b = 3 - (5/2)4. b = 3 - (10). b = -7. Comprueba si la intersección con el eje y es realmente -7. Escribe la ecuación: y = 5/2 x - 7 
2/3 se convierte en -3/2 -6/5 se convierte en 5/6 3 (o 3/1 — es lo mismo) se convierte en -1/3 -1/2 se convierte en 2 
Introduce tu pendiente y coordenadas en la ecuación anterior. Multiplica la pendiente (metro) con la coordenada x del punto. Resta ese valor de la coordenada y del punto. Ya has resuelto la ecuación para B; la intersección con el eje y. 


Resuelve la pendiente. La pendiente de nuestra nueva línea se convierte en el inverso negativo de la pendiente de la línea anterior. Determine la pendiente de la línea anterior: 2y = -4x + 9 jalar "2" fuera de ambos lados: y = -4/2x + 9/2 la pendiente es -4/2 o -2. El recíproco negativo de -2 es 1/2. reorganiza tu ecuación. b = y - mx. Completa y resuelve. b = -1 - (1/2)8. b = -1 - (4). b = -5. Comprueba que tu intersección con el eje y es realmente -5. Escribe la ecuación: y = 1/2 x - 5
Hallar la ecuación de una recta
Contenido
Para hallar la ecuación de una recta tienes necesito dos cosas:a) un punto en la línea; y b) la pendiente (a veces también la pendiente) de la recta. Pero la forma en que recopila estos dos datos y lo que hace con ellos después puede ser muy diferente según la situación. En aras de la simplicidad, este artículo se centrará en ecuaciones de la forma y = mx + b en vez de (y - y1) = m(x - x1).
Pasos
Método 1 de 5: Información general
1. Sepa qué buscar.Antes de que pueda buscar la comparación, necesita saber con certeza qué está tratando de encontrar. Tenga en cuenta lo siguiente:
- Los puntos se clasifican como par ordenado, como (-7, -8) o (-2,-6).
- El primer número en un par ordenado es el coordenada x. Esta es la posición horizontal del punto (cuántas unidades a la izquierda o derecha del origen).
- El segundo número en un par ordenado es el coordenada y. Esta es la posición vertical del punto (cuántas unidades hacia arriba o hacia abajo desde el origen).
- El Pendiente entre los dos puntos se llama "La pendiente" — en otras palabras, qué tan lejos tienes que subir (o bajar) y a la derecha (o a la izquierda) para llegar de un punto a otro.
- dos lineas son paralelo si no se cruzan.
- Dos lineas son perpendiculares entre si si se cruzan en un ángulo recto (90 grados).
2. Determine qué tipo de tarea está tratando.
3. Aborde el problema usando uno de los cuatro métodos a continuación. Dependiendo de la información dada, hay diferentes formas de resolverlo.
Método 2 de 5:Se dan un punto y una pendiente

1. Encuentra la intersección de tu ecuación con el eje y. La intersección con el eje y (o la variable B en nuestra ecuación) es el punto en el que la línea se cruza con el eje y. Puede calcular la intersección con el eje y reorganizando la ecuación para resolver B. Nuestra nueva ecuación ahora se ve así: b = y - mx.
- Ingrese su pendiente y coordenadas en la ecuación anterior.
- Multiplica la pendiente (metro) con la coordenada x del punto.
- Resta ese valor de la coordenada y del punto.
- Ahora tu tienes B resuelta, la intersección con el eje y.

2. Escribe la fórmula:y = ____ x + ____ , junto con los espacios en blanco.

3. Rellena el primer espacio vacío, el de la x, con la pendiente.

4. Complete el segundo espacio en blanco con la intersección con el eje y que calculaste antes.

5. Resolver el problema de ejemplo. "Dado el punto (6, -5) y la pendiente 2/3, ¿cuál es la ecuación de la recta?"
Método 3 de 5: se otorgan dos puntos
1. Calcular la pendiente entre dos puntos. La pendiente también se llama Pendiente y puede pensar en esto como la velocidad a la que algo se mueve a lo largo de un eje y y un eje x imaginarios. La ecuación de la pendiente es: (Y2 - Y1) / (X2 - X1)
- Toma los dos puntos y utilízalos en la ecuación (dos coordenadas significan dos y-valores y dos X-valores). No importa qué coordenadas ingrese primero, siempre que lo haga de manera consistente. Algunos ejemplos:
- Puntos (3, 8) y (7, 12). (Y2 - Y1) / (X2 - X1) = 12 - 8 / 7 - 3 = 4/4, o 1.
- Puntos (5, 5) y (9, 2). (Y2 - Y1) / (X2 - X1) = 2 - 5 / 9 - 5 = -3/4.

2. Elija un conjunto de coordenadas para el resto del problema. Tache o cubra el otro conjunto de coordenadas para que no las use accidentalmente.

3. Calcula la intersección con el eje y de tu ecuación. Nuevamente, reordene la fórmula y = mx + b para obtener una ecuación de la forma b = y – mx. Sigue siendo la misma ecuación; lo acabas de reorganizar.

4. Escribe la fórmula:y = ____ x + ____ , incluidos los espacios en blanco.

5. Rellena el primer espacio vacío, el de la x, con la pendiente.

6. Complete el segundo espacio en blanco con la intersección con el eje y.

7. Resolver el problema de ejemplo. "Dados los puntos (6, -5) y (8, -12), ¿cuál es la ecuación de la recta?"
Método 4 de 5: cuando se dan un punto y una línea paralela
1. Determinar la pendiente de la recta paralela. Recuerda que la pendiente es el coeficiente de X por lo cual y no tiene coeficiente.
- En una ecuación como y = 3/4 x + 7, la pendiente es 3/4.
- En una ecuación como y = 3x - 2, la pendiente es 3.
- En una ecuación como y = 3x, la pendiente sigue siendo 3.
- En una ecuación como y = 7, la pendiente es cero (porque no hay x en el problema).
- En una ecuación como y = x - 7, la pendiente es 1.
- En una ecuación como -3x + 4y = 8, la pendiente es 3/4.
- Para encontrar la pendiente de una ecuación como esta, simplemente reorganícela para que la y está aislado:
- 4y = 3x + 8
- Divide ambos lados por 4: y = 3/4x + 2

2. Calcula la intersección con el eje y, usando la pendiente del primer paso y la ecuación b = y - mx.

3. Escribe la fórmula:y = ____ x + ____ , con los espacios en blanco.

4. Rellena el primer espacio vacío, antes de la x, con la pendiente que determinaste en el paso 1.Lo notable de las líneas paralelas es que tienen la misma pendiente, por lo que terminas con lo que empezaste.

5. Rellene la intersección con el eje y en el segundo espacio vacío.
6. Resolver el problema de ejemplo. "Dado el punto (4, 3) y la recta paralela 5x - 2y = 1; cual es la ecuacion de la recta?"
Método 5 de 5: Con un punto dado y una recta perpendicular
1. Encuentre la pendiente de la recta dada. Consulte los ejemplos anteriores para obtener más información.

2. Encuentra el recíproco negativo de esa pendiente. En otras palabras, darle la vuelta y cambiar el signo. El punto con líneas perpendiculares es que tienen una pendiente inversa negativa, por lo que tendrás que hacer cambios en la pendiente antes de poder usarla.

3. Calcular la intersección con el eje y usando la pendiente del paso 2 y la ecuación b = y - mx

4. Escribe la fórmula:y = ____ x + ____ , con los espacios en blanco.

5. Rellene el primer espacio vacío, antes de la x, con la pendiente que calculó en el paso 2.

6. Rellene la intersección con el eje y en el segundo espacio vacío.
7. Resolver el problema de ejemplo. "Dados (8, -1) y y la perpendicular 4x + 2y = 9; cual es la ecuacion de la recta?"
Artículos sobre el tema. "Hallar la ecuación de una recta"
Оцените, пожалуйста статью
Popular