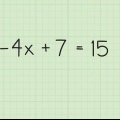Por ejemplo, suponga que tiene la ecuación 3X + -2X + 14X=0. por un X fuera de paréntesis, obtenemos X(3X + -2X + 14)=0. 
En nuestra declaración de ejemplo, completamos nuestros valores un, b y C (respectivamente 3, -2 y 14) en la ecuación cuadrática en: Respuesta 1: Respuesta 2: 
La razón por la que esto funciona tiene que ver con el hecho fundamental de que cualquier número multiplicado por cero es igual a cero. Cuando conviertes la ecuación a la forma X(hacha + bx + C)=0, esencialmente divide los dos en partes: una parte es el X-variable fuera de paréntesis y la otra es el cuadrado dentro de paréntesis. Si alguna de estas partes es igual a cero, entonces también lo es toda la ecuación. Entonces, si las dos respuestas al cuadrado dentro de los paréntesis hacen que esa parte sea cero, entonces las respuestas a la ecuación cúbica también harán que la parte fuera de los paréntesis sea igual a cero. 

En nuestra declaración de ejemplo, a=2 y d=6. Los factores de 2 son 1 y 2. Los factores de 6 son 1, 2, 3 y 6. 
En nuestra ecuación calculas los factores de a (1, 2) sobre los factores de D (1, 2, 3, 6) y obtienes la siguiente lista: 1, 1/2, 1/3, 1/6, 2 y 2/3. Ahora añadimos los números negativos a la lista para que quede completa: 1, -1, 1/2, -1/2, 1/3, -1/3, 1/6, -1/6, 2, -2, 2/3 y -2/3. La solución entera de nuestra ecuación cúbica se puede encontrar en algún lugar de esta lista. 
El uso compartido sintético es un tema complejo: siga el enlace de arriba para obtener más información. Aquí hay un ejemplo de cómo encontrar una de las soluciones a nuestra ecuación cúbica usando la división sintética: 

En nuestro problema de ejemplo, lo resolvemos de la siguiente manera: 
En nuestro problema de ejemplo, lo resolvemos de la siguiente manera: 
En nuestro problema de ejemplo, determinar Δ es muy simple, porque tanto Δ0 como Δ1=0. Resolvemos esto de la siguiente manera: 
En nuestro problema de ejemplo, encontramos C como sigue: 
En nuestro problema de ejemplo, podemos resolver esto comprobando la respuesta cuando n es igual a 1, 2 o 3. Las respuestas que obtenemos de estas pruebas son las posibles respuestas a nuestra ecuación cúbica: cualquier solución que produzca 0 después de la sustitución en la ecuación es correcta. Por ejemplo, suponga que obtenemos 1 en respuesta a una de las pruebas, porque ingresando 1 en X - 3X + 3X - 1 da como resultado 0 si la respuesta, entonces 1 una de las respuestas a nuestra ecuación cúbica.
Resolver una ecuación cúbica
Contenido
La primera vez que te encuentras con una ecuación cúbica (de la forma hacha + bx + cx + D=0) puede parecer casi irresoluble. Sin embargo, este método para resolver ecuaciones cúbicas existe desde hace siglos! Fue descubierta en el siglo XVI por los matemáticos italianos Niccolò Tartaglia y Gerolamo Cardano. Fue una de las primeras fórmulas desconocidas para los antiguos griegos y romanos. Resolver ecuaciones cúbicas puede ser muy difícil, pero con el enfoque correcto (y suficiente conocimiento básico), incluso las ecuaciones cúbicas más complicadas pueden ser domesticadas.
Pasos
Método 1 de 3: resolverlo con la fórmula abc

1. Comprobar si la ecuación cúbica contiene una constante. Como se indicó anteriormente, las ecuaciones cúbicas tienen la forma hacha + bx + cx + D=0. antes de Cristo, y D puede ser 0 sin cambiar si es o no una ecuación cúbica, lo que significa esencialmente que una ecuación no tiene que constar de todos los términos bx, cx o D ser una ecuacion cubica. Comienzas a aplicar este método relativamente simple de resolver ecuaciones cúbicas comprobando primero si tu ecuación tiene una constante (a D-donde el). Es esto no es el caso, entonces puedes de fórmula abc para encontrar las respuestas de la ecuación con un poco de matemáticas.
- Si la ecuación contiene una constante, tendrá que usar un método diferente. Vea a continuación los enfoques alternativos.

2. disolver un X fuera de la ecuación. Dado que su ecuación no contiene una constante, cada término de la ecuación tiene un X-variable. Esto significa que un X se puede factorizar fuera de la ecuación para simplificarla. Haz esto y reescribe tu ecuación en la forma X(hacha + bx + C).

3. Use la fórmula abc para resolver los términos entre paréntesis. Es posible que haya notado que los términos de su nueva ecuación entre paréntesis tienen la forma de una ecuación cuadrática (hacha + bx + C). Esto significa que podemos encontrar los valores para los cuales la ecuación cuadrática es igual a cero por un, b y C en la fórmula abc ({-B +/-√ (B- 4C.A)}/2a). Esto encontrará dos de las respuestas de su ecuación cúbica.
- {-B +/-√ (B- 4C.A)}/2a
- {-(-2) +/-√ ((-2)-4(3)(14))}/2(3)
- {2 +/-√ (4 - (12)(14))}/6
- {2 +/-√ (4 - (168)}/6
- {2 +/-√ (-164)}/6
- {2 + √(-164)}/6
- {2 + 12.8I}/6
- {2 - 12.8I}/6

4. Use cero y las respuestas cuadráticas como respuestas a su ecuación cúbica. Las ecuaciones cuadriláteras tienen dos soluciones, pero las ecuaciones cúbicas tienen tres. Ya tienes dos: estas son las respuestas que encontraste al resolver la "ecuación cuadrática" entre paréntesis. En aquellos casos en que una ecuación sea apropiada para este `fuera de paréntesis`, la tercera respuesta siempre será 0 son. Felicidades, acabas de resolver una ecuación cúbica.
Método 2 de 3: resolver usando listas de factores

1. Asegúrate de que tu ecuación cúbica tenga una constante. Si bien el método anterior es útil porque no requiere que aprendas nuevas habilidades matemáticas, no siempre funcionará para resolver ecuaciones cúbicas. Si tu ecuación está en la forma hacha + bx + cx + D=0 estado, y D es distinto de cero, los paréntesis no funcionarán y necesitará este método o el de la siguiente parte.
- Por ejemplo, suponga que tiene la ecuación dada 2X + 9X + 13X=-6. En este caso, un 0 a la derecha del signo igual requerirá agregar 6 a ambos lados. Nuestra nueva ecuación es 2X + 9X + 13X + 6=0, D=6, por lo que no podemos usar los paréntesis de la parte anterior.

2. Determinar los factores de a y D. Para resolver la ecuación cúbica, comienza determinando los factores de a (el coeficiente de la X condiciones D (la constante al final de la ecuación). Como recordatorio, los factores son aquellos números que multiplicados juntos forman otro número. Por ejemplo, porque tu 6 surge de la multiplicación 6 &hora; 1 y 2 × 3, son 1, 2, 3 y 6 factores de 6.

3. Comparte los factores de a por los factores de D. Ahora enumeras todos los valores que obtienes al dividir cada factor a por cualquier factor D. Esto generalmente da como resultado muchas fracciones y algunos números enteros. Las soluciones enteras de tu ecuación cúbica serán uno de los enteros de la lista o el número negativo de uno de estos números.

4. Use el uso compartido sintético para verificar manualmente sus respuestas. Una vez que haya compilado la lista de valores, puede encontrar las soluciones enteras para su ecuación cúbica ingresando rápidamente manualmente cada número entero y verificando cuáles son iguales a cero. Si no quiere perder tiempo en esto, hay un método un poco más rápido de acuerdo con una técnica llamada intercambio sintético. La esencia es que divides los enteros por el original a B C y D coeficientes de tu ecuacion cubica. Si te queda un resto de 0, tu valor es una de las soluciones de la ecuación cúbica.
- -1 | 2 9 13 6
- __| -2-7-6
- __| 2 7 6 0
- Como terminamos con un 0 como resto, sabemos que una de las soluciones de nuestra ecuación cúbica es el número entero -1 es.
Método 3 de 3: Usar el `discriminante`

1. Escriba los valores de a B C y D. En este método para encontrar las soluciones de una ecuación cúbica, nos basaremos en gran medida en los coeficientes de los términos de nuestra ecuación. Por esta razón, es prudente utilizar los términos a B C y D anótalo antes de empezar para que no te olvides de qué se trata cada uno.
- Por ejemplo, para la comparación X - 3X + 3X - 1, escribimos a=1, B=-3, C=3 y D=-1. No olvides que de un X-variable sin coeficiente se supone que el coeficiente es igual a 1.

2. Calcular Δ0=B - 3C.A. Cuando usa el discriminante para resolver ecuaciones cúbicas, necesita matemáticas un poco más avanzadas, pero si sigue el procedimiento cuidadosamente, encontrará que es una herramienta valiosa para resolver esas ecuaciones cúbicas que ya son complicadas. Comience por encontrar Δ0, el primero de varios valores importantes que necesitamos, sustituyendo los valores apropiados en la fórmula B - 3C.A.
- B - 3C.A
- (-3) - 3(1)(3)
- 9 - 3(1)(3)
- 9 - 9=0=Δ0

3. Calcular Δ1=2B - 9A B C + 27aD. La siguiente cantidad importante que necesitamos, Δ1, requiere un poco más de trabajo, pero se puede encontrar de la misma manera que Δ0. Sustituye los valores correctos en la fórmula 2B - 9A B C + 27aD por el valor de Δ1.
- 2(-3) - 9(1)(-3)(3) + 27(1)(-1)
- 2(-27) - 9(-9) + 27(-1)
- -54 + 81 - 27
- 81 - 81=0=Δ1

4. Calcular Δ=Δ1 - 4Δ0) ÷ -27a. Luego calculamos el discriminante de la ecuación cúbica a partir de los valores para Δ0 y Δ1. Un discriminante es simplemente un número que nos dice algo sobre las respuestas de un polinomio (inconscientemente puede que ya conozcas el discriminante cuadrático: B - 4C.A). En el caso de la ecuación cúbica, si el discriminante es positivo, entonces la ecuación tiene tres soluciones reales. Si el discriminante es cero, entonces la ecuación tiene una o dos soluciones reales, y algunas de esas soluciones son compartidas. Si es negativa, entonces la ecuación tiene una sola solución. (Una ecuación cúbica siempre tiene una solución real, porque la gráfica siempre es al menos una vez con la X-cortes de eje.)
- Δ1 - 4Δ0) ÷ -27a
- (0) - 4(0)) -27(1)
- 0 - 0 27
- 0=Δ, entonces nuestra ecuación tiene 1 o 2 respuestas.

5. calcular C=√(√((Δ1 - 4Δ0) + Δ1)/ 2). El último valor importante a calcular es C. Con esta importante cantidad, finalmente podemos encontrar las tres soluciones. Resuelva esto como de costumbre, sustituyendo Δ1 y Δ0 donde sea necesario.
- √(√((Δ1 - 4Δ0) + Δ1)/ 2)
- √(√((0 - 4(0)) + (0))/ 2)
- √(√((0 - 0) + (0))/ 2)
- 0=C

6. Calcula las tres respuestas con tus variables. Las respuestas a tu ecuación cúbica están dadas por la fórmula (B + uC + (Δ0/uC)) / 3a, por lo cual Uds=(-1 + √(-3))/2 y norte es 1, 2 o 3. Ingrese sus valores donde sea necesario para resolver esto; esto requiere muchas matemáticas, pero debería darle tres posibles respuestas!
Artículos sobre el tema. "Resolver una ecuación cúbica"
Оцените, пожалуйста статью
Similar
Popular