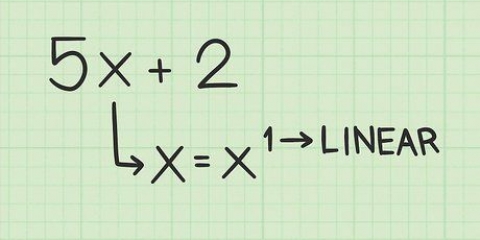Dividir polinomios sintéticamente: 12 pasos (con fotos)

Contenido

Pasos
Consejos

La división sintética es un método abreviado de dividir polinomios en el que se dividen los coeficientes de los polinomios para eliminar variables y exponentes. Esto le permite trabajar durante este cálculo de la misma manera que con la división larga normal. Si quieres saber cómo dividir polinomios sintéticamente, sigue los siguientes pasos.

Pasos

Imagen titulada Dividir polinomios usando la división sintética Paso 1

1. Escribe el problema. Por ejemplo, divides x + 2x - 4x + 8 entre x + 2. Escribe la primera ecuación cuadrática, el dividendo, en el numerador y escribe la segunda ecuación, el divisor, en el denominador.

Imagen titulada Dividir polinomios usando la división sintética Paso 2

2. Invierte el signo de la constante en el divisor. La constante en el divisor, x + 2, es positiva por lo que el inverso del signo de la constante es -2.

Imagen titulada Dividir polinomios usando la división sintética Paso 3

3. Coloque este número fuera de la parte fuera del signo de división. El signo de división parece un revés"yo." Coloque el término -2 a la izquierda de este símbolo.

Imagen titulada Dividir polinomios usando la división sintética Paso 4

4. Anote todos los coeficientes del dividendo dentro del signo de división. Escribe los términos de izquierda a derecha tal como aparecen. Esto se ve así: -2| 12-48.

Imagen titulada Dividir polinomios usando la división sintética Paso 5

5. Bajar el primer coeficiente. Coloque el primer coeficiente, 1, debajo de sí mismo. Esto se ve así:

-2| 1 2 -4 8
↓
1

Imagen titulada Dividir polinomios usando la división sintética Paso 6

6. Multiplica el primer coeficiente por el divisor y colócalo debajo del segundo coeficiente. Multiplica 1 por -2 y escribe el producto -2 debajo del segundo término, 2. Esto se ve así:

-2| 1 2 -4 8
-2
1

Imagen titulada Dividir polinomios usando la división sintética Paso 7

7. Suma el segundo coeficiente y escribe la respuesta debajo del producto. Ahora toma el segundo coeficiente, 2, y súmalo a -2. Escribes el resultado 0 debajo de los dos números, al igual que con la división larga. Esto es lo que parece:

-2| 1 2 -4 8
-2
1 0

Imagen titulada Dividir polinomios usando la división sintética Paso 8

8. Multiplica la suma por el divisor y coloca el resultado debajo del tercer coeficiente. Ahora toma la suma, 0, y multiplícala por el divisor, -2. Coloque el resultado 0 debajo de 4, el tercer coeficiente. Esto es lo que parece:

-2| 1 2 -4 8
-2 0
1

Imagen titulada Dividir polinomios usando la división sintética Paso 9

9. Suma el producto y el tercer coeficiente y escribe el resultado debajo del producto. Sume 0 a -4 y escriba la respuesta -4 debajo de 0. Esto es lo que parece:

-2| 1 2 -4 8
-2 0
1 0 -4

Imagen titulada Dividir polinomios usando la división sintética Paso 10

10. Multiplique este número por el divisor, escríbalo debajo del último coeficiente y súmelo al coeficiente. Ahora multiplica -4 por -2 y escribe la respuesta 8 debajo del cuarto coeficiente, 8, y suma esto al cuarto coeficiente. 8 + 8 = 16, entonces este es tu resto. Escribe el número debajo del producto. Esto es lo que parece:

-2| 1 2 -4 8
-2 0 8
1 0 -4 |dieciséis

Imagen titulada Dividir polinomios usando la división sintética Paso 11

11. Coloque cada uno de los nuevos coeficientes junto a una variable con una potencia menor que las variables originales. En este caso, la primera suma, es 1, y se coloca junto a una x elevada a la segunda potencia (1 menos que 3). La segunda suma, 0, se coloca junto a una x, pero el resultado es 0, por lo que este término se puede eliminar. Y el tercer coeficiente, -4, se convierte en una constante, un número sin variable, porque la variable original era igual a x. Puedes escribir una R al lado del 16, porque este es el resto. Así es como se verá esto:

-2| 1 2 -4 8
-2 0 8
1 0 -4 |dieciséis
X + 0X - 4 R 16

X - 4R16

Imagen titulada Dividir polinomios usando la división sintética Paso 12

12. Anota la respuesta final. Este es el nuevo polinomio, x - 4, más el resto, 16 como numerador y x + 2 como denominador. Así es como se ve: x - 4 +16/(x +2).

Consejos

Para comprobar tu respuesta, multiplica el cociente por el divisor y suma el resto. Este debe ser el mismo que el polinomio original.
(divisor)(cociente)+(resto)
(X + 2)(X - 4) + 16
Multiplique por el primer método externo, el último interno.
(X - 4X + 2X - 8) + 16
X + 2X - 4X - 8 + 16
X + 2X - 4X + 8