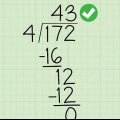
Cabe 15 en 34? Sí, claro, y así podemos empezar a calcular la respuesta. (El primer número no tiene que encajar perfectamente, solo tiene que ser más pequeño que el segundo número). 
Necesitamos resolver 34 ÷ 15, o `¿cuántas veces cabe 15 en 34?`? Estás buscando un número que puedas multiplicar por 15 para obtener un número menor que 34, pero bastante cercano: Obras 1? 15 x 1 = 15, eso es menos de 34, pero sigue adivinando. obras 2? 15x2 = 30. Esto sigue siendo menos de 34, por lo que 2 es una mejor respuesta que 1. obras 3? 15 x 3 = 45, mayor que 34. Demasiado alto! la respuesta es 2. 
Como estás calculando 34 ÷ 15, escribirías como respuesta, 2, en la línea de respuesta arriba del `4`. 
Tu respuesta fue 2 y el número más pequeño en el problema es 15, así que calculamos 2 x 15 = 30. Escribe `30` debajo de `34`. 
Resuelva 34 – 30 y escriba la respuesta a continuación en una nueva línea. la respuesta es 4. Este 4 sigue siendo `el resto` después de dividir 34 entre 15 dos veces, así que lo usaremos en el próximo paso. 
Deje el 4 donde está y baje el `7` de `3472` para hacer 47. 
Resolvemos: 47 ÷ 15: 47 es mayor que nuestro último número, por lo que la respuesta será mayor. Intentemos cuatro: 15 x 4 = 60. no, demasiado grande! En su lugar, intentamos tres: 15 x 3 = 45. Más pequeño que 47 pero cerca de él. Perfecto. La respuesta es 3, así que lo escribimos arriba del `7` en la línea de respuesta. (Si terminamos con una suma como 13 ÷ 15, donde el primer número es más pequeño, tenemos que bajar un tercer dígito antes de poder resolverlo). 
Recuerda, calculamos 47 ÷ 15 = 3, y ahora queremos encontrar lo que queda: 3 x 15 = 45, así que escribe `45` debajo de 47. 47 - 45 = 2. Escribe `2` debajo de 45. 
El siguiente problema es 2 ÷ 15, que no tiene mucho sentido. Baja un número para que sea 22 ÷ 15. 15 cabe en 22 una vez, así que escribimos `1` como el último dígito de la respuesta. Nuestra respuesta es ahora 231. 
1 x 15 = 15, así que escribe 15 debajo de 22. Calcula 22 - 15 = 7. No hay más números que eliminar, así que en lugar de seguir dividiendo escribimos `resto 7` después de nuestra respuesta. La respuesta final: 3472 ÷ 15 = 231 resto 7.


Si encuentra esto difícil, simplemente cuente por triplicado y agregue un 0 al final. Cuente hasta que sea más alto que el número más grande en el problema (143) y deténgase ahí. 
30 (un dedo), 60 (dos dedos), 90 (tres dedos), 120 (cuatro dedos). Entonces 30x cuatro = 120. 150 (cinco dedos), entonces 30 x cinco = 150. 4 y 5 son las dos respuestas más probables a nuestro problema. 
27 x 4 = 108 27 x 5 = 135 
27 x 6 = 162. Esto es más alto que 143, por lo que no puede ser la respuesta correcta. 27 x 5 estuvo más cerca sin pasarse, entonces 143 ÷ 27 = 5 (más un resto 8, porque 143-135 = 8).
Dividir por un número con dos o más dígitos
Contenido
Dividir por un número con dos o más dígitos es muy similar a la división larga con un dígito, pero toma un poco más de tiempo y requiere un poco más de práctica. Dado que la mayoría de nosotros no recordamos la tabla del 47, esto requiere algunas conjeturas, pero hay un buen truco que puedes aprender para hacer esto más rápido. También se vuelve más fácil con un poco de práctica, así que no te frustres si parece lento al principio.
Pasos
Parte 1 de 2: dividir por un número de dos dígitos

1. Mira el primer dígito del número mayor. Escribe el problema como una división larga. Como un problema de división más simple, básicamente miras el número más pequeño y te preguntas: "¿Encaja en el primer dígito del número más grande??`
- Supongamos que tiene el problema 3472 ÷ 15. Se adapta a 15 en 3? Dado que 15 es definitivamente mayor que 3, la respuesta es `no` y pasemos al siguiente paso.

2. Mira los dos primeros números. Dado que un número de dos dígitos no puede caber en un número de un dígito, veamos ahora dos dígitos, tal como lo haríamos con un problema de división normal. Si aún es imposible dividir, entonces tendrás que mirar los primeros tres dígitos, pero en nuestro ejemplo no es necesario:

3. Usa algunas conjeturas. Comprueba cuántas veces cabe el primer número en el otro. Puede que ya sepas la respuesta, pero si no, haz una estimación y comprueba tu respuesta con una multiplicación.

4. Escribe la respuesta arriba del último número que usaste. Escribir esto como una división larga debería ser familiar.

5. Multiplique su respuesta por el número más pequeño. Esto es lo mismo que la división larga normal, pero aquí estamos usando un número de dos dígitos.

6. Resta ambos números entre sí. Lo último que escribiste quedó debajo del número mayor original (o parte de él). Trátelo como una suma menos y escriba la respuesta debajo en una nueva línea.

7. Bajar el siguiente número. Al igual que un problema de división normal, seguimos calculando el siguiente dígito de la respuesta hasta que terminamos.

8. Resuelve el siguiente subproblema. Para obtener el siguiente número, repita los mismos pasos anteriores para el nuevo problema. Puede volver a estimar para encontrar la respuesta:

9. Continuar con la división larga. Repita la división larga como lo hicimos antes para multiplicar nuestra respuesta por el número más pequeño, escriba el resultado debajo del número más grande y réstelo para obtener el resto siguiente.

10. Determinar el último dígito. Como antes, bajamos el siguiente dígito del problema original para poder resolver el siguiente subproblema. Repita los pasos anteriores hasta que encuentre cada dígito de la respuesta.

11. determinar el resto. Ahora solo una suma menos para encontrar el descanso final, y hemos terminado. De hecho, si la respuesta a la suma menos es 0, no tienes que escribir ningún resto.

Parte 2 de 2: Aprendiendo a estimar bien

1. Redondear a la decena mas cercana. No siempre es fácil ver cuántas veces cabe un número de dos dígitos en un número mayor. Un truco útil es redondear al múltiplo de 10 más cercano para que sea más fácil adivinar. Esto es útil para problemas de divisiones más pequeñas o divisiones largas.
- Por ejemplo, digamos que necesitamos resolver 143 ÷ 27, pero no sabemos cuántas veces cabe 27 en 143. Entonces imaginemos que tenemos que resolver 143 ÷ 30.

2. Cuenta el número más pequeño con tus dedos. En nuestro ejemplo podemos empezar a calcular con 30 y no con 27. Contar en pasos de 30 es bastante fácil una vez que aprendes esto: 30, 60, 90, 120, 150.

3. Determine las dos respuestas más probables. El número no encajaba exactamente en 143, pero sí conocemos números que están cerca: 120 y 150. Veamos cuántos dedos tenemos que contar para llegar allí:

4. Prueba esos dos números con el problema real. Ahora que tenemos dos buenas conjeturas, podemos probarlas en el problema original, 143 ÷ 27:

5. Asegúrate de que no puedas acercarte más. Dado que ambos números terminan por debajo de 143, podemos intentar acercarnos aún más al intentar una multiplicación más:

Consejos
- Si no desea multiplicar a mano durante la división larga, intente dividir el problema en números y resolver cada parte de memoria. Por ejemplo, 14 x 16 = (14 x 10) + (14 x 6). Anota 14 x 10 = 140 para que no te olvides. Entonces: 14 x 6 = (10 x 6) + (4 x 6). 10 x 6 = 60 y 4 x 6 = 24. Haz 140 + 60 + 24 = 224 y tienes la respuesta.
Advertencias
- Si en algún momento su suma menos da como resultado un número mayor que el divisor, entonces su estimación no fue lo suficientemente alta. Borre todo ese paso e intente estimar más grande.
- Si en algún momento su suma menos resultó en un negativo número, entonces su estimación fue demasiado alta. Borre todo ese paso e intente estimar más pequeño.
Otros recursos
Artículos sobre el tema. "Dividir por un número con dos o más dígitos"
Оцените, пожалуйста статью
Popular