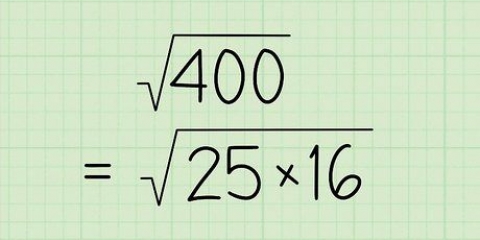Instrucciones de paso a paso gratis 
La única excepción a esta regla es el propio número 2, que, al ser divisible por sí mismo y por 1, también es primo. 2 es el único número primo par. 
Por ejemplo, si quisiéramos usar este método para probar si 11 es primo o no, tendríamos que dividir 11 entre 3, 4, 5, 6, 7, 8, 9 y 10, buscando cada vez una respuesta entera. sin resto. Como ninguno de estos números encaja completamente en 11, podemos decir que 11 es un primo es. 
Examinemos los factores de 100. 100 = 1 × 100, 2 × 50, 4 × 25, 5 × 20, 10 × 10, 20 × 5, 25 × 4, 50 × 2 y 100 × 1. Tenga en cuenta que después de 10 × 10, los factores son los mismos que para 10 × 10, solo que al revés. En general, podemos ignorar los factores de n mayor que sqrt(n) porque son simplemente una continuación de factores menores que sqrt(n). Probemos un ejemplo. Si n = 37, entonces no necesitamos probar todos los números del 3 al 36 para determinar si n es primo. En cambio, solo necesitamos mirar los números entre 2 y sqrt (37) (redondeado hacia arriba). sqrt(37) = 6.08 – vamos a redondear esto a 7. 37 no es completamente divisible por 3, 4, 5, 6 y 7, por lo que podemos decir con confianza que es un número primo es. 
Esto significa que todos los factores pares, así como aquellos que son múltiplos de números primos, se pueden omitir. Por ejemplo, intentemos determinar si 103 es primo o no. La raíz cuadrada de 103 es 11 (redondeado hacia arriba). Los números primos entre 2 y 11 son 3, 5, 7 y 11. 4, 6, 8 y 10 son pares y 9 es un múltiplo de 3, un número primo, así que podemos saltarnos este. Al hacer esto, reducimos nuestra lista de posibles factores a solo 4 números! 103 no es completamente divisible por 3, 5, 7 u 11, por lo que ahora sabemos que 103 es un número primo es. 
Un ejemplo: ¿100 es un número primo o no?. Supongamos que tomamos 3 como valor de prueba: esto está entre 2 y n-1, por lo que es suficiente. 
Otro método es calcular a, y luego dividir por n, luego usar el resto como respuesta. Las calculadoras especializadas con una función de módulo pueden ser muy útiles al dividir números grandes, ya que pueden calcular directamente el resto de una división. Usando una calculadora de este tipo en nuestro ejemplo, podemos ver que 3/100 tiene un resto de 1. Entonces, 3 (mod 100) es 1. 
En nuestro ejemplo calculamos 3 con un módulo de 100. 3 es un número muy, muy grande - 515,377,520,732,011,331,036,461,129,765,621,272,702,107,522,001 - tan grande que se vuelve muy difícil trabajar con él. En lugar de usar la respuesta de 48 dígitos para 3, será mejor que la escribamos como un exponente, así que (((((((3)*3))))*3)). Recuerda que tomando el exponente de un exponente da el efecto de multiplicar los exponentes ((x) = x). Ahora podemos determinar el resto. Comience a resolver para ((((((3)*3))))*3)) en el conjunto interior de paréntesis y salga, dividiendo cada paso por 100. Una vez que hayamos encontrado el resto, lo usaremos para el próximo paso en lugar de como la respuesta real. Vea abajo: ((((((9)*3))))*3)) - 9/100 no tiene resto, así que podemos continuar. ((((((27))))*3)) - 27/100 no tiene resto, así que podemos continuar. (((((729)))*3)) - 729/100 = 7 R 29. nuestro resto es 29. Pasamos al siguiente paso, no 729. ((((29=841))*3)) - 841/100 = 8 R 41. Usaremos nuestro resto 41 nuevamente en el próximo paso. (((41 = 1681)*3)) - 1681/100 = 16 R 81. Usaremos nuestro resto 81 en el próximo paso. ((81*3 = 243)) - 243/100 = 2 R 43. Usaremos nuestro resto 43 en el próximo paso. (43 = 1849) - 1849/100 = 18 R 49. Usaremos nuestro resto 49 en el próximo paso. 49 = 2401 - 2401/100 = 24 R 1. nuestro resto final es 1. En otras palabras, 3 (mod 100) = 1. Tenga en cuenta que esta es la misma respuesta que calculamos en el paso anterior! 
En nuestro ejemplo, 3 (mod 100) = 1 y 3 (mod 100) = 3. 1 ≠ 3, entonces podemos decir que 100 es un número compuesto. 
Supongamos que queremos determinar si n = 321 es un número primo. 321 - 1 = 320, que podemos expresar como 2×5. En este caso n = 321 es un número adecuado. Determinar n – 1 para n = 371 puede requerir un valor grande para d, lo que hace que todo el proceso sea más difícil en una etapa posterior. 371 - 1 = 370 = 2 × 185 
En nuestro ejemplo con n = 321, elegimos a = 100. 
En nuestro ejemplo con n = 321, a (mod n) = 100 (mod 321). 100 = 10 000 000 000 (módulo 321) = 313. Usamos una calculadora especial, o el método abreviado con un exponente como se describió anteriormente, para encontrar el resto de 100/321. Como no obtuvimos 1 ni -1, no podemos decir con certeza que n es primo. Pero hay más que debemos hacer: sigue leyendo. 
Como recordatorio, en nuestro ejemplo, el valor de a es igual a 100, el valor de s es 6 y el de d5. Procederemos con las pruebas como se indica a continuación: 100 = 1×10. 1×10 (mod. 321) = 64. 64 ` 1 o -1. Mantenga la calma. 100 = 1×10. 1×10 (módulo 321) = 244. 244 ≠ 1 o -1. En este punto podemos parar. s - 1 = 6 - 1 = 5. Ahora hemos llegado a 4d = 2, y no hay potencias de 2 por d bajo 5d. Como ninguno de nuestros cálculos dio como respuesta 1 o -1, podemos decir que n = 321 a compuesto número es. 
Datos1 = 1 Datos2 = 2 
Calcular el IMM MMI1 = Número de prueba 2 ^ -1 Número de prueba de modulación 1 MMI2 = Prueba Número1 ^ -1 Mod Prueba Número2 Solo para primos (habrá un resultado para no primos, pero ese no es el MMI): MMI1 = (Número de prueba2 ^ (Número de prueba1-2)) %Número de prueba1 MMI2 = (Número de prueba 1 ^ (Número de prueba-2)) % Número de prueba 2 Entonces: MMI1 = (97^33) %35 MMI2 = (35^95) %97 
Para el MMI1 F(1) = Número de prueba 2 % Número de prueba 1 = 97 % 35 = 27 F(2) = F(1) * F(1) % Número de prueba 1 = 27 * 27 % 35 = 29 F(4) = F(2) * F(2) % Número de prueba 1 = 29 * 29 % 35 = 1 F(8) = F(4) * F(4) % Testnumber1 = 1 * 1 % 35 = 1 F(16) =F(8) * F(8) % Testnumber1 = 1 * 1 % 35 = 1 F(32) = F(16) * F(16) % Número de prueba 1 = 1 * 1 % 35 = 1 Calcule el logaritmo binario de Testnumber1 - 2 35 -2 = 33 (10001) base 2 MMI1 = F(33) = F(32) * F(1) módulo 35 MMI1 = F(33) = 1 * 27 Modo 35 MMI1 = 27 Para MMI2 F(1) = Número de prueba 1 % Número de prueba 2 = 35 % 97 = 35 F(2) = F(1) * F(1) % Número de prueba 2 = 35 * 35 mod 97 = 61 F(4) = F(2) * F(2) % Número de prueba 2 = 61 * 61 mod 97 = 35 F(8)= F(4) * F(4) % Prueba Número2 = 35 * 35 mod 97 = 61 F(16) = F(8) * F(8) % Número de prueba2 = 61 * 61 mod 97 = 35 F(32)= F(16) * F(16) % Prueba Número2 = 35 * 35 mod 97 = 61 F(64)= F(32) * F(32) % Prueba Número2 = 61 * 61 mod 97 = 35 F(128) = F(64) * F(64) % Número de prueba 2 = 35 * 35 mod 97 = 61 Calcule el logaritmo binario de TestNumber2 - 2 97 - 2 = 95 = (1011111) base 2 MMI2 = (((((F(64) * F(16) % 97) * F(8) % 97) * F(4) % 97) * F(2) % 97) * F(1) % 97 ) MMI2 = ((((((35 * 35) %97) * 61) % 97) * 35% 97) * 61% 97) * 35% 97) MMI2 = 61 
Respuesta = (1 * 97 * 27 + 2 * 35 * 61) % (97 * 35) Respuesta = (2619 + 4270) % 3395 Respuesta = 99 
Calcular (Respuesta - Datos1) % Prueba Número1 99 -1 % 35 = 28 Como 28 es mayor que 0, 35 no es primo 
Calcular (Respuesta - Datos2) % Prueba Número2 99 - 2% 97 = 0 Como 0 es igual a 0, 97 es un primo potencial 
Si el paso 7 es igual a 0: usa otro "prueba número 1" si TestNumber1 no es primo. Use otro TestNumber1 donde un TestNumber1 es en realidad un número primo.En este caso, los pasos 6 y 7 son iguales a 0. Use diferentes puntos de datos para data1 y data2. Si el paso 7 es siempre igual a 0, entonces la probabilidad de que el número 2 sea primo es muy alta. Se sabe que los pasos 1 a 7 son incorrectos en ciertos casos cuando el primer número no es primo y el segundo es un factor primo del número no primo "prueba número 1".Funciona en todos los escenarios donde ambos números son primos. La razón por la que se repiten los pasos del 1 al 7 es porque hay algunos escenarios en los que, incluso si TestNumber1 no es primo y TestNumber2 no es primo, cualquiera de los números del Paso 7 sigue siendo cero.Estas condiciones son raras.Al cambiar TestNumber1 a otro número no primo, si TestNumber2 no es primo, TestNumber2 ya no será igual a cero, en el paso 7. Con excepción del caso en que "prueba número 1" es un factor de TestNumber2, los números primos siempre serán cero en el paso 7.
Comprobar si un número es primo
Contenido
Los números primos son números que solo son divisibles por sí mismos y se llaman 1 – otros números compuesto números. Cuando se trata de probar si un número es primo, hay varias opciones. Algunos de estos métodos son relativamente simples pero definitivamente no prácticos para números más grandes. Otras pruebas que se utilizan a menudo son en realidad algoritmos completos basados en un probabilidad que a veces clasifican erróneamente un número como primo. Continúe leyendo en el paso 1 para aprender cómo probarse a sí mismo si está tratando con un número primo.
Pasos
Método 1 de 4: prueba dividiendo
Probar dividiendo es, con mucho, la forma más fácil de probar un número. Para números pequeños suele ser también la forma más rápida. La prueba se basa en la definición de un número primo: un número es primo si solo es divisible por sí mismo y 1.
1. Pareja norte es el numero que quieres probar. Divide el número n entre todos los enteros divisibles posibles. Para números más grandes como n=101, es extremadamente poco práctico dividir por todos los enteros posibles menores que n. Afortunadamente, existen varios trucos para reducir el número de factores a probar.
2. Determinar si norte incluso es. Todos los números pares son completamente divisibles por 2. Por lo tanto, si n es par, se puede decir que n es un número compuesto (y por lo tanto no es un número primo). Para determinar rápidamente si un número es par, solo debes fijarte en el último dígito. Si el último dígito es 2, 4, 6, 8 o 0, entonces el número es par y no primo.
3. Parte norte por cualquier número entre 2 y n-1. Dado que un número primo no tiene más factores que él mismo y 1 y que los factores de los números enteros son menores que su producto, comprobar la divisibilidad de un número entero menor que n y mayor que 2 determinará si n es primo. Empezamos después de 2 porque los números pares (múltiplos de 2) no pueden ser primos. Esto está lejos de ser una forma eficiente de probar, como verá a continuación.
4. Para ahorrar tiempo, pruebe solo hasta sqrt (norte), redondeado. Probar un número n al verificar todos los números entre 2 y n-1 puede consumir mucho tiempo rápidamente. Por ejemplo, si quisiéramos comprobar si 103 es primo con este método, tendríamos que dividir por 3, 4, 5, 6, 7 ... etc., todo el camino a 102! Afortunadamente no es necesario probar así. En la práctica solo es necesario probar por los factores entre 2 y la raíz cuadrada de n. Si la raíz cuadrada de n no es un número, redondearlo al entero más cercano y probar con este número. Vea a continuación una explicación:
5. Para ahorrar aún más tiempo, solo usamos factores primos. Es posible acortar aún más el proceso de prueba por división al no incluir aquellos factores que no son primos. Por definición, cualquier número compuesto puede expresarse como el producto de dos o más números primos. Por lo tanto, no es necesario dividir el número n entre un número compuesto; esto es equivalente a dividir entre números primos varias veces. Entonces, podemos reducir aún más la lista de posibles factores a solo números primos más pequeños que sqrt (n).
Método 2 de 4: Usando el pequeño teorema de Fermat
En 1640, el matemático francés Pierre de Fermat planteó por primera vez un teorema (que ahora lleva su nombre) que puede ser muy útil para determinar si un número es primo o no. Técnicamente, la prueba de Fermat está destinada a verificar si un número es compuesto, en lugar de primo. Esto se debe a que la prueba con "Certeza absoluta" puede mostrar que un número es compuesto, pero sólo un "probabilidad" si un número es primo. El pequeño teorema de Fermat es útil en situaciones en las que tratar de dividir entre no es práctico y cuando se dispone de una lista de números que son excepciones al teorema.
1. Suponer norte el numero es para probar. Usas esta prueba para determinar si un número dado n es primo. Pero como se mencionó anteriormente, este teorema puede ocasionalmente caracterizar erróneamente ciertos compuestos como números primos. Es importante tener esto en cuenta y comprobar su respuesta, que se explicará más adelante.
2. Elige un entero a entre 2 y norte-1 (incluido). El número entero exacto que elija no es importante. Dado que los parámetros para a incluyen 2 y n-1, también puede usar estos.
3. calcular a (modificación norte). Calcular esta expresión requiere cierto conocimiento de un sistema matemático llamado matemáticas modulares. En las matemáticas modulares, los números vuelven a cero al alcanzar cierto valor, conocido como módulo. Puedes pensar en esto como un reloj: eventualmente la manecilla del reloj volverá a la 1 en punto después de las 12 en punto, no a la 1 en punto. El módulo se anota como (mod norte). Así que en este paso calculas con un módulo de n.
4. Si calculamos esto a mano, usamos el exponente como notación abreviada. Si no tiene una calculadora con una función de módulo, use la notación exponencial para facilitar el procedimiento de determinar el resto. Vea abajo:
5. Comprobar si a (modificación norte) = a (modificación norte). Si no, entonces n es compuesto. Si es cierto, entonces n es probablemente, (pero no estoy seguro) un número primo. Repetir la prueba con diferentes valores para a puede hacer que el resultado sea más seguro, pero hay números compuestos raros que satisfacen el teorema de Fermat para todo valores de un. Estos se llaman los números de Carmichael - el más pequeño de estos números es 561.
6. Use los números de Carmichael para estar seguro de su resultado. Saber qué números satisfacen la secuencia de Carmichael antes de continuar puede ahorrarle muchos dolores de cabeza sobre si un número es primo o no. En general, los números de Carmichael son el producto de números primos individuales, donde para todos los números primos se cumple que si p es un divisor de n, entonces p-1 también es un divisor de n-1. La lista en línea de números de Carmichael puede ser muy útil para determinar si un número es primo usando el pequeño teorema de Fermat.
Método 3 de 4: usar la prueba de Miller-Rabin
La prueba de Miller-Rabin funciona de la misma manera que el pequeño teorema de Fermat, pero trata mejor con números anómalos como los números de Carmichael.
1. Pareja norte es un número impar cuya primalidad queremos probar. Como en los métodos indicados anteriormente, n es la variable que queremos determinar la primalidad de.
2. Ocupado norte-1 descuento en la forma 2 × D por lo cual D es impar. El número n es primo si es impar. Entonces n - 1 debe ser par. Como n - 1 es par, se puede escribir como una potencia de 2 por un número impar . Entonces, 4 = 2 × 1; 80 = 2 × 5; y así.
3. Elige cualquier número a entre 2 y norte-1. El número exacto que elija no importa, solo que debe ser menor que n y mayor que 1.
4. calcular a (modificación norte). Si a = 1 o -1 (módulo norte), entonces resistenorte la prueba de Miller-Rabin y es probablemente un número primo. Al igual que con el Pequeño Teorema de Fermat, esta prueba no puede determinar la primalidad de un número con absoluta certeza, pero necesita pruebas adicionales para hacerlo.
5. Como el resultado no es igual a 1 o -1, calculea, a,... y así sucesivamente, hasta aD. Calcular a elevado a d por , hasta 2. Si uno de estos es igual a 1 o -1 (mod norte), entonces resiste norte la prueba de Miller-Rabin y es probablemente principal. Una vez que haya determinado que n pasa la prueba, verifique su respuesta (vea el paso a continuación). Si n no pasa ninguna de estas pruebas, entonces es un compuesto número.
6. Si norte cumple con la prueba de Miller-Rabin, luego repita para los otros valores de a. Si ha encontrado que el valor de n bien puede ser primo, intente nuevamente con un valor aleatorio diferente para a para confirmar el resultado de la prueba. Si n es realmente primo, esto se cumplirá para cualquier valor de a. Si n es un número compuesto, fallará para las tres cuartas partes de los valores de un. Esto le da más certeza que con el Pequeño Teorema de Fermat, en el que ciertos números compuestos (los números de Carmichael) pasan la prueba para cada valor de un.
Método 4 de 4: usar el teorema del resto chino
1. Elige dos números. Uno de los números no es primo y el segundo es el número que se está probando para la primalidad.
- "prueba número 1" = 35
- Número de prueba 2 = 97
2. Elija dos puntos de datos mayores que cero y menores que TestNumber1, respectivamente TestNumber2. no pueden ser iguales.
3. Calcule el MMI (inverso multiplicativo matemático) para TestNumber1 y TestNumber2
4. Cree una tabla binaria para cada MMI hasta Log2 del Módulo
5. Calcular (Data1 * TestNumber2 * MMI1 + Data2 * TestNumber1 * MMI2) % (TestNumber1 * TestNumber)
6. Comprobar si "prueba número 1" no es primo 1
7. Comprobar si TestNumber2 es un número primo
8. Repita los pasos 1 a 7 al menos dos veces más.
Consejos
- Los 168 números primos por debajo de 1000 son: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79 , 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211 , 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359 , 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509 , 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853 , 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997
- Cuando intentar dividir es más lento que los métodos más sofisticados, sigue siendo eficiente para números más pequeños. Incluso cuando se prueban números más grandes, no es raro verificar primero los números pequeños antes de cambiar a los métodos más avanzados.
Artículos de primera necesidad
- Papel, bolígrafo, lápiz y/o calculadora para hacer ejercicio
Artículos sobre el tema. "Comprobar si un número es primo"
Оцените, пожалуйста статью
Similar
Popular
