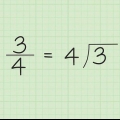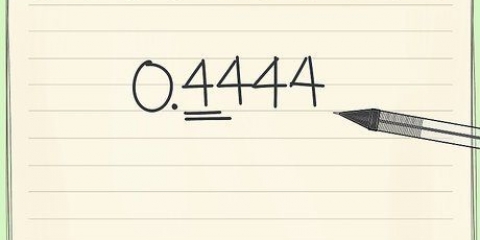8 8 8 Reescribe esto como: 64 8 1 No necesitas potencias de 8 mayores que tu número original (en este caso 98). Como 8 = 512 y 512 es mayor que 98, podemos dejar eso fuera de la tabla. 
98
÷ 64 8 1
= 1 ← Este es el primer dígito de tu número octal. 
98 34
÷ 64 8 1
= 1 
98 34
÷ ÷ 64 8 1
= = 1 4 
98 34 2
÷ ÷ ÷ 64 8 1
= = = 1 4 2 La respuesta final: 98 con base 10 = 142 con base 8. Puedes escribir esto como 9810 = 1428 
2x8 = 2x1 = 2 4x8 = 4x8 = 32 1x8 = 1x64 = 64 2 + 32 + 64 = 98, el número con el que empezamos. 
Selecciona esta pieza: 327 7 7
÷ ÷ ÷ 64 8 1
= = = 5 0 7 la respuesta es 507. (Pista: 0 puede ser con seguridad la respuesta a un subproblema.) 

En nuestro ejemplo: 670 8 = 83. 
En nuestro ejemplo: 670 ÷ 8 = 83 resto 6. Nuestro número octal hasta ahora es ???6. Si su calculadora tiene un "módulo" o "modificación"-botón, puede determinar este valor ingresando: "670 modelo 8." 
En nuestro ejemplo: La respuesta al último subproblema es 83. 83 ÷ 8 = 10 resto 3. Nuestro número octal hasta ahora es ??36. 
En nuestro ejemplo: La respuesta al último subproblema es 10. 10 ÷ 8 = 1 resto 2. Nuestro número octal hasta ahora es ?236. 
En nuestro ejemplo: La respuesta al último subproblema es 1. 1 ÷ 8 = 0 resto 1. Nuestra respuesta final es el número octal 1236. Podemos escribir esto como 12368 para mostrar que este es un número octal. 
Empiezas con una pila de 670 unidades. El primer subproblema divide esto en grupos, 8 unidades por grupo. Lo que queda, el resto, no cabe en los ochos del octal. Entonces debe estar en el lugar de las unidades. Ahora tome la pila de grupos y divídala en secciones de 8 grupos cada una. Cada sección ahora tiene 8 grupos con 8 unidades cada uno, o 64 unidades en total. El resto no cabe aquí, por lo que no pertenece al lugar de los 64 números. Debe estar en el lugar de los 8 números. Esto continúa hasta que haya determinado el número entero.
Convertir un número decimal a octal
Contenido
Octal es el sistema numérico de base 8, donde solo se usan los dígitos del 0 al 7. La mayor ventaja es la facilidad con la que se convierte a binario (base 2), porque cada dígito de un octal se puede escribir como un número binario único de tres dígitos. Convertir de decimal a octal es un poco más complicado, pero no necesita más matemática que una división larga para hacer esto. Comience con el método de división, donde determina cada número dividiéndolo por potencias de 8. El método de descanso es más rápido y usa la misma forma de cálculo, pero puede ser un poco más complicado de entender.
Pasos
Método 1 de 2: Conversión compartiendo

1. Utilice este método para aprender los conceptos. De los dos métodos en esta página, este método es el más fácil de entender. Si ya está acostumbrado a trabajar con diferentes sistemas numéricos, pruebe el siguiente método de descanso, que es un poco más rápido.

2. Escribe el número decimal. Para este ejemplo, convertiremos el número 98 a un octal.

3. Haz una lista de las potencias de 8. No olvides eso "decimal" tiene una base 10 porque cada dígito de un número dentro de este sistema es una potencia de 10. Llamaremos a los primeros 3 dígitos unidades, decenas y centenas, pero también podemos escribir 10, 10 y 10. Los números octales, o aquellos con base 8, usan potencias de 8 en lugar de 10. Escribe algunas de estas potencias de 8 en una línea horizontal, de mayor a menor. Tenga en cuenta que todos estos números están escritos como decimales (base 10):

4. Divide el número decimal por el número con la mayor potencia de 8. Fíjate bien en el número decimal: 98. El nueve en el lugar de las decenas indica que hay 9 decenas en este número. 10 va 9 veces en este numero. Asimismo, con el octal, queremos saber cuántas veces "64" entra en el número final. Divide 98 entre 64 para determinar esto. La forma más fácil de hacer esto es usando una tabla, lea de arriba a abajo:
÷
=

5. determinar el resto. Calcula el resto del problema de la división, o el número que queda y ya no encaja completamente. Escribe tu respuesta en la parte superior de la segunda columna. Esto es lo que queda de tu número después de calcular los primeros dígitos. En nuestro ejemplo, 98 ÷ 64 = 1. Como 1 x 64 = 64, el resto es 98 - 64 = 34. Añade esto a tu mesa:
÷
=

6. Divide el resto por la siguiente potencia de 8. Para determinar el siguiente dígito pasamos a la siguiente potencia de 8. Divide el resto por este número y completa la segunda columna de tu tabla:
÷ ÷
= =

7. Sigue haciendo esto hasta que encuentres la respuesta completa. Como antes, determine el resto de su respuesta y escríbala en la parte superior de la siguiente columna. Sigue dividiendo y determinando el resto hasta que hayas hecho esto para cada columna, incluyendo 8 (las unidades). La última fila es el último número decimal, convertido a octal. Aquí está nuestro ejemplo con la tabla completamente llena (nota que 2 es el resto de 34÷8):
÷ ÷ ÷
= = =

8. Revisa tu trabajo. Haces esto multiplicando cada dígito del octal por la potencia de 8 que representa. A continuación, debe obtener el número original de nuevo. Comprobemos la respuesta, 142:

9. Pruebe el siguiente problema de práctica.Practica el método convirtiendo 327 en un número octal. Cuando creas que has encontrado la respuesta, selecciona el texto invisible a continuación para ver el efecto del problema completo.
÷ ÷ ÷
= = =
Método 2 de 2: Conversión usando el resto

1. Empezar con un número decimal. Empezamos con el número 670.
- Este método es más rápido que la división secuencial. La mayoría de las personas encuentran esto mucho más difícil de entender, y pueden encontrar más cómodo comenzar con el método más simple anterior.

2. Divide este número por 8. Ignora los números después del punto decimal por ahora. Pronto verá por qué este cálculo es útil.

3. determinar el resto. Ahora nosotros tan a menudo como podamos "dividido por 8", queda un pequeño resto. Eso es todo ultimo dígito de nuestro número octal, en el lugar de las unidades (8). El resto siempre es menor que 8, por lo que puede representarse con cualquiera de los otros dígitos.

4. Divide la respuesta al problema de división por 8. Deje el resto a un lado y regrese al problema de compartir. Toma la respuesta y divídela de nuevo por 8. Anota la respuesta y decide el resto. Este es el penúltimo dígito del octal, el lugar 8 = 8s.

5. Dividir por 8 otra vez. Como antes, divide la respuesta del último problema de división por 8 y encuentra el resto. Este es el penúltimo dígito del octal, el 8 = 64 lugar.

6. Repita esto hasta que haya determinado el último número. Si ha calculado el último subproblema, entonces la respuesta es cero. El resto de este problema es el primer dígito del octal. Ahora ha convertido completamente el número decimal.

7. Entiende cómo funciona esto. Si te resulta difícil entender este método, aquí tienes una explicación:
Ejercicios
- Intente convertir los siguientes números decimales usted mismo usando uno de los métodos anteriores. Cuando creas que has encontrado la respuesta, selecciona el texto invisible a la derecha del signo igual para verificar. (Tenga en cuenta que 10 medios decimales y 8 octales.)
- 9910 = 1438
- 36310 = 5538
- 521010 = 121328
- 4756910 = 1347218
Artículos sobre el tema. "Convertir un número decimal a octal"
Оцените, пожалуйста статью
Popular