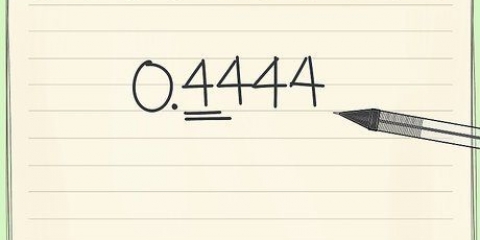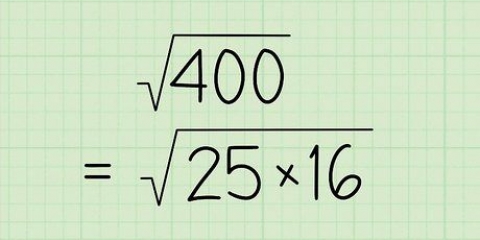Convertir un número decimal a formato binario ieee 754: 11 pasos (con fotos)

A diferencia de los humanos, las computadoras no usan el sistema numérico decimal. Usan un sistema numérico binario o binario con dos dígitos posibles, 0 y 1. Por lo tanto, los números se escriben de manera muy diferente en IEEE 754 (un estándar IEEE para representar números binarios con un punto flotante) que en el sistema decimal tradicional al que estamos acostumbrados. En este artículo, aprenderá a escribir un número con precisión simple o doble de acuerdo con IEEE 754. Para este método, necesita saber cómo convertir números en forma binaria. Si no sabe cómo hacer esto, puede aprenderlo a través del artículo Convertir binario a decimal para estudiar.

Pasos

1. Elija precisión simple o doble. Al escribir un número con precisión simple o doble, los pasos para una conversión exitosa serán los mismos para ambos. El único cambio ocurre al convertir el exponente y la mantisa.

Primero necesitamos entender qué significa precisión simple. En la vista de punto flotante, cualquier número (0 o 1) se considera un `bit`. Por lo tanto, una sola precisión tiene un total de 32 bits divididos en tres sujetos diferentes. Estos sujetos constan de un signo (1 bit), un exponente (8 bits) y una mantisa o fracción (23 bits).
La precisión doble, por otro lado, tiene la misma configuración y las mismas tres partes que la precisión simple; la única diferencia es que será un número más grande y más preciso. En este caso el signo será de 1 bit, el exponente de 11 bits y la mantisa de 52 bits.
En este ejemplo vamos a convertir el número 85.125 a precisión simple según el IEEE 754.

2. Separe el número antes y después del punto decimal. Tome el número que desea convertir y separe el número para que le quede un número entero y un número decimal. En este ejemplo asumimos el número 85.125. Puedes separar esto en el entero 85 y el decimal 0.125.

3. Convertir el número entero a un número binario. Este será el 85 de 85.125, que se convertirá en 1010101 cuando se convierta a binario.

4. Convertir la parte decimal a un número binario. Esto es entonces 0,125 de 85,125, que se convierte en 0,001 en notación binaria.

5. Combina las dos partes del número convertido a números binarios. El numero 85 es binario por ejemplo 1010101 y la parte decimal 0.125 es binario 0.001. Si los combina con un punto decimal, obtiene 1010101,001 como respuesta final.

6. Convertir número binario a notación binaria científica. Puede convertir el número a notación binaria científica moviendo el punto decimal hacia la izquierda hasta que esté a la derecha del primer bit. Estos números están normalizados, lo que significa que el bit inicial siempre será 1. En cuanto al exponente, la cantidad de veces que mueves el decimal es el exponente en notación binaria científica.

Recuerde que mover el decimal a la izquierda produce un exponente positivo, mientras que mover el decimal a la derecha produce un exponente negativo.

En nuestro ejemplo, debe mover el decimal seis veces para colocarlo a la derecha del primer bit. La notación resultante se convierte entonces en

01, 010101001 * 2 6

${ estilo de visualización 01.010101001 * 2 ^ {6}}$ . Este número se utilizará en los siguientes pasos.

7. Determine el signo del número y muéstrelo en notación binaria. Ahora determinará si el número original es positivo o negativo. Si el número es positivo, escribe ese bit como 0 y si es negativo, como 1. Como el número original es 85.125 positivo, escribe ese bit como 0. Este es ahora el primer bit del total de 32 bits en su representación de precisión simple según IEEE 754.

8. Determinar el exponente basado en la precisión. Hay un sesgo fijo para precisión simple y doble. El sesgo del exponente de precisión simple es 127, lo que significa que tenemos que sumar el exponente binario encontrado previamente. Así que el exponente que vas a usar es 127 + 6 = 133.

La precisión doble, como su nombre lo indica, es más precisa y puede contener números más grandes. Por lo tanto, el sesgo del exponente 1023. Aquí se aplican los mismos pasos que se usan para la precisión simple, por lo que el exponente que puede usar para determinar la precisión doble es 1029.

9. Convertir el exponente a binario. Después de determinar su exponente final, debe convertirlo a binario para que pueda usarse en la conversión IEEE 754. En el ejemplo puedes convertir el 133 que encontraste en el último paso a 10000101.

10. Determinar la mantisa. El aspecto de la mantisa, o la tercera parte de la conversión IEEE 754, es el resto del número después del decimal de la notación binaria científica. Simplemente omites el 1 al frente y copias la parte decimal del número multiplicado por dos. No se requiere conversión binaria! En el ejemplo, la mantisa se convierte en 010101001 de

01, 010101001 * 2 6

${ estilo de visualización 01.010101001 * 2 ^ {6}}$ .

11. Finalmente, combine tres partes en un solo número.

Finalmente, combinas todo lo que hemos calculado hasta ahora en tu conversión. El número comenzará primero con un 0 o un 1 que determinó en el paso 7 según el signo. En el ejemplo se empieza con un 0.

Luego tienes el exponente que determinaste en el paso 9. En el ejemplo, el exponente es 10000101.

Luego viene la mantisa, la tercera y última parte de la conversión. Obtuviste esto antes cuando tomaste la parte decimal de la conversión binaria. En el ejemplo, la mantisa es 010101001.

Finalmente, combina estos números entre sí. El orden es signo-exponente-mantisa. Después de conectar estos tres números binarios, complete el resto de la mantisa con ceros.

Por ejemplo, si 85.125 se convierte al formato binario IEEE 754, la solución es 0 10000101 01010100100000000000000.