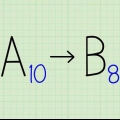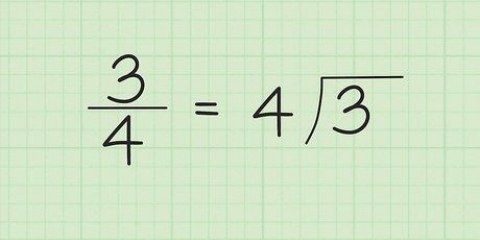16 = 1.048.576 16 = 65.536 16 = 4.096 16 = 256 16 = 16 Si el número decimal que está convirtiendo es mayor que 1.048.576, luego calcule las potencias superiores de 16 y agréguelas a la lista. 
Por ejemplo, si usted 495 convierte a hexadecimal, luego elige 256 de la lista anterior. 
En nuestro ejemplo, 495 ÷ 256 = 1.93... , pero solo nos interesa el número entero 1. Tu respuesta es el primer dígito del número hexadecimal. En este caso, como hemos dividido por 256, el 1 es el número en el lugar del "256-es." 
Multiplica tu última respuesta por el divisor. En nuestro ejemplo, 1 x 256 = 256. (En otras palabras, el 1 de nuestro número hexadecimal representa el 256 con la base 10). Resta tu respuesta del dividendo. 495 - 256 = 239. 
239 ÷ 16 = 14. Nuevamente, ignoramos todos los lugares decimales. Este es el segundo dígito de nuestro número hexadecimal, el "16-y." Cualquier número del 0 al 15 se puede representar como un solo dígito hexadecimal. Convertimos a la notación correcta al final de este método. 
14x16 = 224. 239 - 224 = 15, entonces el resto es 15. 
El último "figura" de nuestro número hexadecimal es 15, en el lugar del "unidades." 
Los números del 0 al 9 siguen siendo los mismos. 10 = A; 11 = B; 12 = C; 13 = D; 14 = E; 15 = F En nuestro ejemplo terminamos con los números (1)(14)(15). En notación adecuada, esto se convierte en el número hexadecimal 1EF. 
1EF → (1)(14)(15) De derecha a izquierda, 15 está en 16 = 1ra posición. 15x1 = 15. El siguiente dígito de la izquierda está en la posición 16 = 16. 14x16 = 224. El siguiente dígito está en la posición 16 = 256. 1 x 256 = 256. Los sumamos todos juntos, 256 + 224 + 15 = 495, nuestro número original. 

Para encontrar el resto, multiplica la respuesta por el divisor, luego resta el resultado del dividendo. En nuestro ejemplo, 317.547 - (19.846x16) = 11. Convierta el dígito a formato hexadecimal usando la tabla de conversión de números pequeños en la parte superior de la página de este artículo. 11 vueltas B en nuestro ejemplo. 
En nuestro ejemplo, 19.846 / 16 = 1.240. resto = 19.846 - (1.240x16) = 6. Este es el penúltimo dígito de nuestro número hexadecimal. 
Tome el último cociente y divídalo nuevamente por 16. 1.240 / 16 = 77 restante 8. 77 / 16 = 4 resto 13 = D. 4 < 16, entonces 4 es el primer digito. 
Nuestra última respuesta es 4D86B. Para verificar su trabajo, vuelva a convertir cada dígito al número decimal, multiplíquelo por potencias de 16 y sume los resultados. (4x16) + (13x16) + (8x16) + (6x16) + (11x1) = 317.547, nuestro número decimal original.
Convertir de decimal a hexadecimal
Contenido
El hexadecimal es un sistema numérico de base dieciséis. Esto significa que hay 16 símbolos para indicar un número, con A, B, C, D, E y F sumados a los diez dígitos habituales. Convertir de decimal a hexadecimal es más difícil que al revés. Tómese el tiempo para aprender esto, ya que es más fácil evitar errores una vez que comprenda por qué funciona la conversión.
Conversiones de números pequeños
| Decimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| hexadecimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | a | B | C | D | mi | F |
Pasos
Método 1 de 2: método intuitivo

1. Usa este método si eres nuevo en los números hexadecimales. De los dos enfoques de este artículo, este es el más fácil de seguir para la mayoría de las personas. Si ya estás familiarizado con las diferentes bases, prueba la más rápida método como indicada a continuación.
- Si no está familiarizado con los números hexadecimales, primero aprenda los conceptos básicos.

2. Escribe las potencias de 16. Cada dígito dentro del sistema hexadecimal representa una potencia diferente de 16, al igual que un dígito decimal es una potencia de 10. Esta lista de potencias de 16 será útil al convertir:

3. Encuentra la potencia más alta de 16 que quepa dentro del número decimal. Escriba el número decimal que desea convertir. Utilice la lista anterior como referencia. Encuentra la potencia más alta de 16 que es menor que el número decimal.

4. Divide el número decimal por esta potencia de 16. Deténgase en el número entero e ignore cada dígito después del punto decimal de la respuesta.

5. encuentra el resto. Esto le dice lo que queda del número decimal para convertir. Así es como se puede calcular, al igual que con una división larga:

6. Divide el resto por la siguiente potencia superior de 16. Usa tu lista de potencias de 16 nuevamente como referencia. Continuar así a la menor potencia de 16. Divide el resto por ese valor para encontrar el siguiente dígito de tu número hexadecimal. (Si el resto es menor que este número, el siguiente dígito es 0.)

7. Determinar el resto de nuevo. Como antes, multiplica la respuesta por el divisor y réstalo del dividendo. Este es el resto que aún necesita ser convertido.

8. Repita hasta que tenga un resto de menos de 16. Una vez que el resto es de 0 a 15, se puede expresar con un solo dígito hexadecimal. Escribe esto como el último número.

9. Escribe tu respuesta en la notación correcta. Ahora sabes cuáles son todos los dígitos de tu número hexadecimal. Pero hasta ahora solo los hemos escrito en base diez. Para escribir cada dígito en la notación hexadecimal correcta, conviértalos usando esta guía:

10. Revisa tu trabajo. Verificar tu respuesta es fácil cuando entiendes cómo funcionan los números hexadecimales. Convierta cada dígito nuevamente a la forma decimal y multiplíquelos por la potencia 16 para esa posición base. Esto es lo que tenemos que hacer para nuestro ejemplo:
Método 2 de 2: método rápido (con descanso)

1. Divide el número decimal por 16. Trata esta división como una división entera. En otras palabras, te detienes en una respuesta con un número entero, en lugar de calcular los números decimales.
- Seamos un poco más ambiciosos con este ejemplo, y el número decimal 317.547 convertir. Calcular 317.547 ÷ 16 = 19.846, e ignora los decimales.

2. Escribe el resto en notación hexadecimal. Ahora que dividiste el número por 16, el resto es la parte que ya no se ajusta a la posición de los 16 o más. Por lo tanto, el resto debe llegar a la posición de las unidades, se ultimo dígito del número hexadecimal.

3. Repita este proceso con el cociente. Convertiste el resto a un dígito hexadecimal. Ahora para seguir convirtiendo el cociente, divídelo de nuevo por 16. El resto es el penúltimo dígito del número hexadecimal. Esto funciona con la misma lógica que el anterior: el número original ahora se divide por (16 x 16 =) 256, por lo que el resto es la parte del número que se ajusta a la posición de los 256. Ya sabemos las unidades, el resto debe estar en el lugar de los 16.

4. Repite hasta obtener un cociente menor a 16. No olvides convertir un resto de 10 a 15 en formato hexadecimal. Tenga en cuenta cualquier descanso en el camino. El último cociente (menos de 16) es el primer dígito de tu número. Seguimos con el ejemplo:

5. terminar el numero. Como se mencionó anteriormente, usted determina cada dígito del número hexadecimal de derecha a izquierda. Revisa tu trabajo para asegurarte de que los escribiste en el orden correcto.
Consejos
- Para evitar confusiones al usar los diferentes sistemas numéricos, puede escribir la base como un subíndice. Por ejemplo, 51210 es entonces "512 con base 10," un número decimal ordinario. 512dieciséis medio "512 con base 16," equivalente al número decimal 1.29810.
Artículos sobre el tema. "Convertir de decimal a hexadecimal"
Оцените, пожалуйста статью
Popular