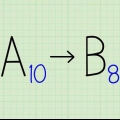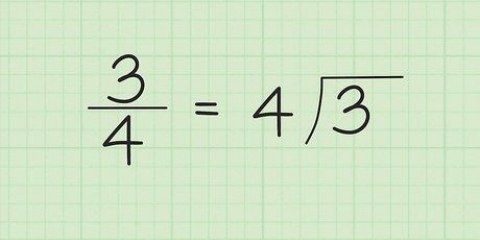Convertir un decimal periódico en una fracción: 9 pasos (con fotos)

Contenido

Pasos
- Parte 1 de 2: convertir decimales periódicos simples
- Parte 2 de 2: convertir números con decimales periódicos y no periódicos

Un decimal periódico, también llamado decimal periódico, es un número decimal que contiene un dígito o grupo de dígitos que se repite indefinidamente a intervalos regulares. Los decimales periódicos pueden ser complicados para trabajar, pero también se pueden convertir a una fracción. A veces, los decimales periódicos se indican con una línea encima de los dígitos periódicos. El número 3,7777 con 7 como dígito repetido, por ejemplo, también se puede escribir como 3.7. Para convertir un número como este en una fracción, escríbalo como una ecuación, multiplique y reste para eliminar el decimal periódico y resuelva la ecuación.

Pasos

Parte 1 de 2: convertir decimales periódicos simples

$Imagen titulada Convertir decimales repetidos en fracciones Paso 1$

1. Encuentra el decimal periódico. Por ejemplo: el número 0.4444 tiene un decimal periódico 4. Es un decimal periódico estándar en el sentido de que no hay una parte que no se repita en el número decimal. Cuente cuántos lugares decimales repetidos (repetitivos) hay en el patrón.

Cuando tu ecuación esté escrita, multiplícala por 10^y`, por lo cualy es igual al número de dígitos repetidos en el patrón.
En el ejemplo de 0.4444, hay un dígito que se repite, así que multiplicas la ecuación por 10^1.
Para un decimal periódico de 0.4545, hay dos números que se repiten y, por lo tanto, multiplicarías tu ecuación por 10 ^ 2.
Para tres números repetidos, multiplique por 10 ^ 3, etc.

$Imagen titulada Convertir decimales repetidos en fracciones Paso 2$

2. Reescribe el decimal como una ecuación. Escríbelo de manera que x sea igual al número original.En este caso, la ecuación es x = 0.4444. Dado que solo hay un dígito en el decimal periódico, multiplique la ecuación por 10 ^ 1 (que es igual a 10).

En el ejemplo: donde x = 0,4444, entonces 10x = 4.4444.

en el ejemplo x = 0,4545 hay dos números que se repiten, así que multiplicas ambos lados de la ecuación por 10^2 (que es igual a 100), lo que te da 100x = 45.4545 obtiene.

$Imagen titulada Convertir decimales repetidos en fracciones Paso 3$

3. Eliminar el decimal periódico. Haces esto restando x de 10x. Recuerda que lo que haces en un lado de la ecuación, lo tienes que hacer en el otro lado, así que:

10x – 1x = 4,4444 – 0,4444

A la izquierda tienes 10x - 1x = 9x. En el lado derecho tienes 4.4444 – 0.4444 = 4

Por lo tanto: 9x = 4

$Imagen titulada Convertir decimales repetidos en fracciones Paso 4$

4. Solución para x. Una vez que sepa a qué equivale 9x, puede determinar a qué equivale x dividiendo ambos lados de la ecuación por 9:

En el lado izquierdo de la ecuación tienes 9x ÷ 9 = x. En el lado derecho de la ecuación tienes 4/9

Es por eso que x = 4/9, y puede ser el decimal periódico 0.4444 escribirse como la fracción 4/9.

$Imagen titulada Convertir decimales repetidos en fracciones Paso 5$

5. Reducir la fracción. Convierte la fracción a su forma más simple (si la hay) dividiendo tanto el numerador como el denominador por el máximo común divisor.

En el ejemplo de 4/9 esa es la forma más simple.

Parte 2 de 2: convertir números con decimales periódicos y no periódicos

$Imagen titulada Convertir decimales repetidos en fracciones Paso 6$

1. Determinar los números repetidos. No es raro que un número tenga dígitos que no se repiten antes del decimal periódico, pero aún se pueden convertir en fracciones.

Tomemos por ejemplo el número 6.215151. Aquí está 6.2 no repetidos, y los números repetidos son 15.
Tenga en cuenta nuevamente cuántos dígitos repetidos hay en el patrón, porque va a multiplicar por 10^y en función de ese número.
En este ejemplo, hay dos números que se repiten, así que multiplique la ecuación por 10^2.

$Imagen titulada Convertir decimales repetidos en fracciones Paso 7$

2. Escribe el problema como una ecuación y resta los decimales periódicos. De nuevo, si x = 6,215151, entonces 100x = 621.5151. Para eliminar los decimales periódicos, resta de ambos lados de la ecuación:

100x-x (= 99x) = 621.5151 – 6.215151 (= 615,3)

Por tanto, 99x = 615,3

$Imagen titulada Convertir decimales repetidos en fracciones Paso 8$

3. Solución para x. Como 99x = 615.3, divide ambos lados de la ecuación por 99. esto te da x = 615,3/99.

$Imagen titulada Convertir decimales repetidos en fracciones Paso 9$

4. Eliminar el decimal en el contador. Haz esto multiplicando el numerador y el denominador por 10^z`, por lo cualz es igual a la cantidad de decimales que tienes que mover para eliminar el decimal. En 615.3 tienes que mover el decimal una posición, lo que significa que multiplicas el numerador y el denominador por 10^1:

615.3×10 / 99x10 = 6153/990

Simplifica la fracción dividiendo el numerador y el denominador por el máximo común divisor (en este caso 3), y obtienes x = 2.051 / 330