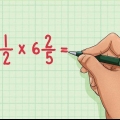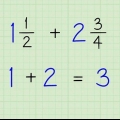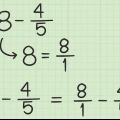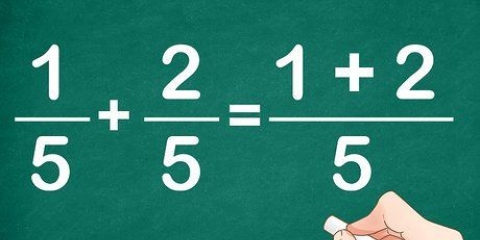Convertir fracciones impropias a números mixtos: 9 pasos (con fotos)

Contenido

Pasos
- Método 1 de 2: convertir una fracción impropia
- Método 2 de 2: resolver problemas de muestra
Consejos

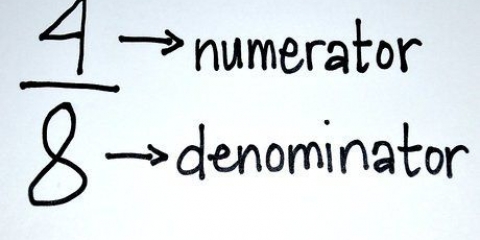
En matemáticas, las fracciones impropias son aquellas en las que el numerador (el número de arriba) es mayor o igual que el denominador (el número de abajo). Para convertir una fracción impropia en un número mixto (usando una fracción y un número entero, como 2 3/4), divide el numerador entre el denominador. Escribe la parte completa de la respuesta junto a una fracción, con el resto en el numerador y el denominador original debajo; ahora tienes una fracción mixta!

Pasos

Método 1 de 2: convertir una fracción impropia

$Imagen titulada Convertir fracciones impropias en números mixtos Paso 1$

1. Divide el numerador entre el denominador. Empieza a escribir tu fracción impropia. Luego divide el numerador por el denominador; en otras palabras, calcula la suma de la división como se muestra. No olvides anotar el resto.

Tomemos un ejemplo. Digamos que necesitamos convertir la fracción 7/5 en un número mixto. Primero dividimos 7 por 5, así:
7/5 → 7 ÷ 5 = 1 R2

$Imagen titulada Convertir fracciones impropias en números mixtos Paso 2$

2. Escribe el número entero de la respuesta. El número entero de tu número mixto (el número grande a la izquierda de tu fracción) es la respuesta al número entero de la suma de la división. En otras palabras, escribe la respuesta de la división sin el resto.

En nuestro ejemplo, omitiríamos el resto y simplemente 1 escríbelo (ya que nuestra respuesta es 1 R2).

$Imagen titulada Convertir fracciones impropias en números mixtos Paso 3$

3. Hacer una fracción del resto y el denominador original. Ahora necesitamos encontrar la parte fraccionaria del número mixto. Pon el resto de la división en el numerador y usa el mismo denominador de tu fracción impropia original. Pon esta fracción al lado de tu número entero y tienes tu número mixto!

En nuestro ejemplo, el resto es igual a 2. Si ponemos esto como numerador arriba del denominador original (5), obtenemos 2/5. Ponemos esto junto a nuestra respuesta al número entero (1) y obtenemos el número mixto final. Como sigue:

1 2/5.

$Imagen titulada Convertir fracciones impropias en números mixtos Paso 4$

4. Para volver a convertir esto en una fracción impropia, sumamos el número entero al numerador. Los números mixtos se ven bien en papel y son fáciles de leer, pero no siempre son la mejor opción. Por ejemplo, si multiplicamos una fracción y un número mixto, nuestro trabajo será mucho más fácil si volvemos a convertir el número mixto en una fracción impropia. Haces esto simplemente multiplicando el número entero por el denominador y sumando al numerador.

Si queremos hacer una fracción impropia de la respuesta a nuestro ejemplo (1 2/5), podemos hacerlo así:

1 × 5 = 5 → (2 + 5)/5 = 7/5

Método 2 de 2: resolver problemas de muestra

$Imagen titulada Convertir fracciones impropias en números mixtos Paso 5$

1. Convertir 11/4 a un número mixto. Este problema es simple, simplemente resuélvalo exactamente como se indicó anteriormente. Vea a continuación una solución paso a paso.

11/4 — para empezar, necesitamos dividir el numerador por el denominador.
11 ÷ 4 = 2 R 3 — ahora necesitamos hacer una fracción del resto y nuestro denominador original.
11/4 = 2 3/4

$Imagen titulada Convertir fracciones impropias en números mixtos Paso 6$

2. Convierte 99/5 a un número mixto. Estamos lidiando con un contador muy grande aquí, pero no dejes que eso te engañe, el método es exactamente el mismo! Vea abajo:

99/5 - cuantas veces cabe 5 en 99? Como 5 va exactamente 20 veces en 100, puedes suponer que 5 va 19 veces en 99.

99 ÷ 5 = 19 R 4 — ahora solo creamos el número mixto como antes.

99/5 = 19 4/5

$Imagen titulada Convertir fracciones impropias en números mixtos Paso 7$

3. Convertir 6/6 a un número mixto. Hasta ahora solo hemos tratado con fracciones impropias donde el numerador es mayor que el denominador. Pero que pasa cuando ambos son iguales? Vea a continuación para averiguarlo.

6/6: seis van una vez en seis, sin descanso, por supuesto.

6 6 = 1 R0. Dado que una fracción con 0 en el numerador siempre es igual a cero, no necesitamos poner una fracción al lado de nuestro número entero.

6/6 = 1

$Imagen titulada Convertir fracciones impropias en números mixtos Paso 8$

4. Convertir 18/6 a un número mixto. Si el numerador es un múltiplo del denominador, no te preocupes por el resto, solo haz la suma de la división para obtener tu respuesta. Vea abajo.

18/6: como sabemos que 18 es solo 6 × 3, sabemos que tendremos un resto de 0, por lo que no tenemos que preocuparnos por la parte fraccionaria de nuestro número mixto.

18/6 = 3

$Imagen titulada Convertir fracciones impropias en números mixtos Paso 9$

5. Convierte -10/3 en un número mixto. Los números negativos funcionan exactamente igual que los números positivos. Vea abajo:

-10/3

-10 ÷ 3 = -3 R1

-10/3 = -3 1/3

Consejos

Las fracciones impropias no son necesariamente incorrecto. De hecho, a veces son más útiles que los números mixtos. Por ejemplo, si vas a multiplicar dos fracciones, las fracciones impropias son mejores porque solo tienes que multiplicar los numeradores y los denominadores para obtener tu respuesta: p. 1/6 × 7/2 = 7/12. Ahora multiplica 1/6 × 3 1/2, no es muy fácil.
Por otro lado, los números mixtos suelen ser más útiles para describir algo en la vida real. Por ejemplo, una receta requiere 4 1/2 tazas de harina, no 9/2 tazas de harina.