Sumar y restar fracciones

Contenido

Pasos

Sumar y restar fracciones es una habilidad esencial para aprender. Te encuentras con fracciones en todas partes en la vida cotidiana, especialmente en la clase de matemáticas, desde la escuela primaria hasta la universidad. Simplemente siga los pasos a continuación para aprender a sumar y restar fracciones, ya sean fracciones iguales, desiguales, mixtas o impropias. Una vez que has aprendido una forma, todo lo demás es mucho más fácil!

Pasos

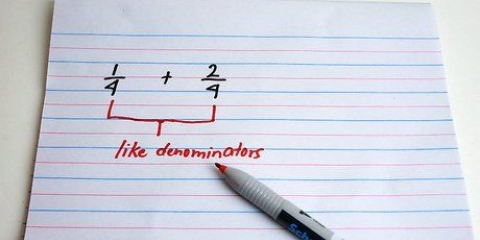
Método 1 de 3: Sumar y restar fracciones con el mismo denominador

$Imagen titulada Sumar y restar fracciones Paso 1$

1. escribe la ecuacion. Si el denominador de las dos fracciones que sumas/restas es el mismo, incluye también este denominador en tu respuesta.

En otras palabras, no tienes que escribir 1/5 y 2/5 como 1/5 + 2/5 = ? Esto se puede notar como (1+2)/5 = ?. El denominador es el mismo y, por lo tanto, solo debe mencionarse una vez. Ambos numeradores están por encima de la línea de puntuación.

$Imagen titulada Sumar y restar fracciones Paso 2$

2. Añadir los contadores juntos. El numerador es el número arriba de la línea fraccionaria. Tomemos el siguiente ejemplo: 1/5 y 2/5; aquí están 1 y 2 nuestros contadores.

Ya sea que escribas 1/5 + 2/5 o 1+2/5, la respuesta es la misma: 3! Finalmente, 1 + 2 = 3.

$Imagen titulada Sumar y restar fracciones Paso 3$

3. Dejar el denominador sin cambios. Nada que sumar, restar, etc, pero sin cambios.

Entonces, siguiendo el mismo ejemplo, el denominador es 5. Eso es todo! Este es el número de abajo de la fracción y la mitad de la respuesta!

$Imagen titulada Sumar y restar fracciones Paso 4$

4. Escribe la respuesta. Ahora todo lo que tienes que hacer es escribir la respuesta! Verás que según el ejemplo anterior, la respuesta es 3/5.

cual era el contador? 3. y el denominador? 5. Entonces, 1/5 + 2/5, o 1+2/5, es igual 3/5.

Método 2 de 3: Sumar y restar fracciones con diferentes denominadores

$Imagen titulada Sumar y restar fracciones Paso 5$

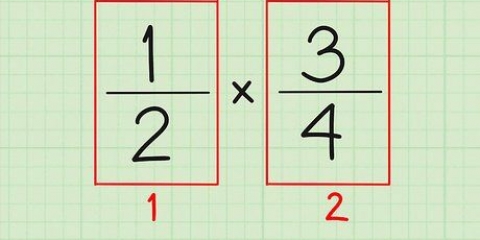
1. Encuentra el Mínimo Común Múltiplo (MCM) de los denominadores. Este es el número más pequeño que ambos denominadores tienen en común. Toma las fracciones 2/3 y 3/4. cuales son los denominadores? 3 y 4. Para encontrar el LCF de ambos, use una de las siguientes 3 formas:

Escribe los múltiplos. Los múltiplos de 3 son 3, 6, 9, 12, 15, 18...y así. Los múltiplos de 4? 4, 8, 12, 16, 20, etc. ¿Cuál es el número más bajo que ocurre en ambos conjuntos?? 12! Ese es tu mínimo común múltiplo o tu kgv.
Factorización en factores primos. Si sabes qué son los factores primos, puedes usar la factorización. Aquí determinas con qué números primos puedes multiplicar un número determinado mediante la multiplicación "para hacer". Para 3, los factores son 3 y 1. Para 4, los factores primos son 2 y 2. Luego los multiplicas juntos, así que 3 x 2 x 2 = 12. tu kgf!

Multiplica ambos números para obtener elpequeño números. En algunos casos, como este, puedes simplemente multiplicar ambos números: 3 x 4 = 12. Pero si sus denominadores son números grandes, esto no puede suceder! No puedes simplemente hacer 56 x 44 y pasar a 2464 como respuesta! No está mal, pero es incómodo.

$Imagen titulada Sumar y restar fracciones Paso 6$

2. multiplica el denominador por el numero que necesitas para obtener el lcg. En otras palabras, desea que cada denominador sea el mismo número: el kgv. Para nuestro ejemplo, esto debe ser 12. 4x3 = 12. Este es el denominador de nuestra respuesta final.

Entonces 2/3 se convierte en 2/3 x 4 y 3/4 se convierte en 3/4 x 3. Eso significa que ahora tenemos 2/12 y 3/12. Pero aún no hemos terminado!

Notarás que en este caso, los denominadores se han multiplicado juntos. Esto funciona en esta situación, pero no siempre. A veces tendrás que buscar números más pequeños para encontrar el LCF.

Y en otros casos, con números pequeños, todo lo que tienes que hacer es multiplicar los denominadores entre sí.

$Imagen titulada Sumar y restar fracciones Paso 7$

3. Multiplica el numerador por ese número también. Si multiplicas el denominador de una fracción por un número, también tendrás que multiplicar el numerador por el mismo número. Lo que hicimos en el último paso fue solo una parte de la multiplicación necesaria.

Teníamos 2/3x4 y 3/4x3 como primer paso; para agregar el segundo paso, en realidad es 2 x 4/3 x 4 y 3 x 3/4 x 3. Eso significa que 8/12 y 9/12 son nuestros nuevos números. Perfecto!

$Imagen titulada Sumar y restar fracciones Paso 8$

4. Suma (o resta) los numeradores para obtener tu respuesta. Para sumar 8/12 a 9/12, solo suma los numeradores. No olvides: dejas el denominador solo. El número que obtuviste con el LCF es tu denominador final.

En este ejemplo se cumple: 8+9/12 = 17/12. Para convertir esto en un número mixto, resta el denominador del numerador y mira lo que te queda. Es decir, en este caso, 17/12 = 1 5/12

Método 3 de 3: Sumar y restar fracciones mixtas e impropias

$Imagen titulada Sumar y restar fracciones Paso 9$

1. Convierte tus fracciones mixtas a fracciones impropias. Una fracción mixta es un número entero seguido de una fracción, como en el ejemplo anterior (1 5/12). Una fracción impropia es una fracción con un numerador mayor que denominador. Un ejemplo de esto es 17/12.

Como ejemplo tomamos 13/12 y 17/8.

$Imagen titulada Sumar y restar fracciones Paso 10$

2. Encuentra el denominador común. Recuerda las tres formas de encontrar el mcg de los denominadores? Determinando los múltiplos, usando factores primos o multiplicando los denominadores.

Averigüemos cuáles son los múltiplos de 12 y 8. ¿Cuál es el número más pequeño en el que caben ambos números?? 24. 8, 16, 24 y 12, 24 – bingo!

$Imagen titulada Sumar y restar fracciones Paso 11$

3. Multiplica los numeradores por los denominadores para obtener la fracción igual. Ambos denominadores ahora deben convertirse a 24. Cómo hacer 24 de 12? multiplicalo por 2. De 8 a 24? multiplicalo por 3. Pero no olvides que también tienes que multiplicar los numeradores!

Entonces 13 x 2/12 x 2 = 26/24. Y 17 x 3/8 x 3 = 51/24. Hemos recorrido un largo camino para resolver el problema!

$Imagen titulada Sumar y restar fracciones Paso 12$

4. Suma y resta de fracciones. Ahora que ambas fracciones tienen el mismo denominador, puedes sumar o restar fácilmente ambas fracciones. Recuerda, deja el denominador en paz!

26/24 + 51/24 = 77/24. Ese es el descanso que estabas buscando! Pero el mostrador es bastante grande....

$Imagen titulada Sumar y restar fracciones Paso 13$

5. Convierta su respuesta en una fracción mixta. Un numerador tan grande es un poco extraño y dificulta tener una idea del tamaño de su fracción. Todo lo que tienes que hacer para resolver eso es dividir el numerador por el denominador y usar el resto como numerador para tu nueva fracción compuesta.

Para este ejemplo: 24 cabe en 77. 3 veces.Entonces, 24 x 3 = 72. Entonces queda un resto de 5! Entonces, ¿cuál es tu respuesta final?? 3 5/24. Eso es todo!