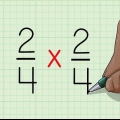(/2) = /2 × /2 o (/2). Elevar al cuadrado cada número da (/4). 
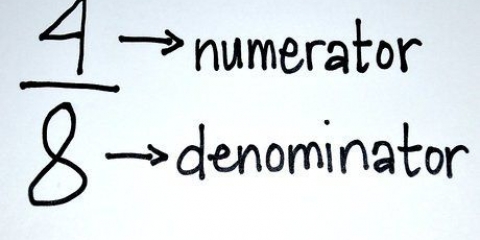
El numerador se queda arriba de la fracción y el denominador se queda abajo. Por ejemplo: (/2) = (/2x2) = (/4). 
Para convertir esto a un número mixto, divide 25 por 4. Esto es 6 (6 x 4 = 24), con un resto de 1. Por lo tanto, el número mixto es 6/4. 

Por ejemplo: (-/4) = (–/4) X (-/4) 
Por ejemplo: (-2) x (-8) = (+16) 
Siguiendo con el ejemplo, la fracción resultante será un número positivo. (-/4) X (-/4) = (+/dieciséis) La costumbre es omitir el signo más de los números positivos. 
Por ejemplo: (/dieciséis) tiene un factor común de cuatro. Divide la fracción por 4: 4/4 = 1, 16/4= 4 Reescribe la fracción simplificada: (/4) 

Por ejemplo: 16 × (/dieciséis) Cuadre los paréntesis y elimine el factor común de 16: dieciséis * /dieciséis * /dieciséis Como estás tratando aquí con un 16 como un número entero y el doble de un 16 en el denominador, puedes eliminar uno de ellos. Reescribe la ecuación simplificada: 12 × /dieciséis simplificar /dieciséis dividiendo por 4: /4 Multiplicar: 12 × /4 = 36/4 Parte: 36/4 = 9 
Por ejemplo: 16 * (/dieciséis) Reescribe con el numerador y el denominador al cuadrado: 16 * (/dieciséis) Resta el exponente en el denominador: dieciséis * /dieciséis Imagina los primeros 16 como un exponente de 1:16. Usando las reglas para restar potencias/exponentes, resta los exponentes entre sí. 16/16, da 16 = 16 o 1/16. Ahora procede con /dieciséis Reescribe y simplifica la fracción: /dieciséis =* /4. Simplificar: 12 × /4 = 36/4 Parte: 36/4 = 9
Elevar fracciones al cuadrado
Contenido
Elevar fracciones al cuadrado es una de las operaciones más sencillas que puedes realizar con fracciones. Es muy similar a elevar al cuadrado números enteros en el sentido de que puedes multiplicar tanto el numerador como el denominador por sí mismos. Hay algunos casos en los que simplificar la fracción antes de elevarla al cuadrado facilita el procedimiento. Si aún no ha aprendido esta habilidad, este artículo proporciona una breve descripción para mejorar su comprensión.
Pasos
Parte 1 de 3: Elevar fracciones al cuadrado

1. Entender cómo elevar números enteros al cuadrado. Cuando ves un número elevado a la segunda potencia, sabes elevar el número al cuadrado. Esto es lo mismo que multiplicar el número por sí mismo. Por ejemplo:
- 5 = 5 × 5 = 25

2. ¿Te das cuenta de que al cuadrarfracciones funciona de la misma manera. Para elevar al cuadrado una fracción, multiplica la fracción por sí misma. Otra forma de pensar en esto es multiplicar el numerador por sí mismo y el denominador por sí mismo. Por ejemplo:

3. Multiplica el numerador por si mismo y el denominador por si mismo. El orden real en el que multipliques estos números por sí mismos no importa, siempre y cuando eleves ambos números al cuadrado. Para mantener las cosas simples, comience con el numerador: simplemente multiplíquelo por sí mismo. luego multiplicas el denominador por si mismo.

4.Simplificar la fracción para terminar esto. Cuando se trata de fracciones, el último paso siempre es simplificar la fracción a su forma más simple o convertir una fracción impropia en un número mixto. Nuestro ejemplo, /4 es una fracción impropia porque el numerador es mayor que el denominador.
Parte 2 de 3: elevar al cuadrado fracciones con números negativos

1. Busque un signo menos delante de la fracción. Si se trata de una fracción negativa, hay un signo menos delante de ella. Es aconsejable poner siempre paréntesis alrededor de un número negativo para que sepa que el signo menos se refiere al número y no pretende ser una suma menos.
- Por ejemplo: (-/4)

2. Multiplica la fracción por sí misma. Eleva al cuadrado la fracción como lo harías normalmente, multiplicando el numerador por sí mismo y luego multiplicando el denominador por sí mismo. También puedes simplemente multiplicar la fracción por sí misma.

3. Comprender que multiplicar dos números negativos juntos da como resultado un número positivo. Cuando hay un signo menos, la fracción entera se vuelve negativa. Cuando elevas al cuadrado la fracción, multiplicas dos números negativos. Cuando se multiplican dos números negativos, el producto siempre es positivo.

4. Eliminar el signo menos después de elevar al cuadrado. Si has elevado al cuadrado la fracción, has multiplicado dos números negativos. Esto significa que la fracción al cuadrado es positiva. No olvides omitir el signo menos en la respuesta final.

5. Simplifica la fracción en la medida de lo posible. El último paso para hacer cálculos con fracciones es simplificar. Las fracciones impropias primero deben simplificarse a números mixtos y luego simplificarse aún más.
Parte 3 de 3: uso de simplificaciones y arreglos rápidos

1. Comprueba si puedes hacer la fracciónsimplificar antes de cuadrarlo. Por lo general, es más fácil simplificar fracciones antes de elevarlas al cuadrado. Recuerda, simplificar una fracción implica dividirla por un factor común hasta que 1 sea el único número que queda que se puede dividir tanto por el numerador como por el denominador. Simplificar una fracción primero significa que no tienes que volver a simplificarla al final, cuando los números son más grandes.
- Por ejemplo: (/dieciséis)
- 12 y 16 se pueden dividir por 4. 12/4 = 3 y 16/4 = 4; así puedes/dieciséis simplificar a /4.
- Ahora puedes hacer la fracción /4 cuadrar.
- (/4) = /dieciséis, que ya no puedes simplificar.
- Para probar esto, elevamos al cuadrado la fracción original sin simplificar:
- (/dieciséis) = (/16x16) = (/256)
- (/256) tiene un factor común de 16. Dividir el numerador y el denominador por 16 simplifica la fracción a (/dieciséis), la misma fracción que obtuvimos al simplificar primero.

2. Aprende cuándo postergar la simplificación de una fracción. ¿Estás lidiando con algo más complejo? ecuaciones, entonces puede ser posible eliminar uno de los factores. En tal caso, por lo tanto, es más conveniente esperar con la simplificación de la fracción. Agregar un factor adicional al ejemplo anterior hace que esto sea más claro.

3. Comprenda cómo hacer esto rápidamente con elexponente. Otra forma de resolver el mismo problema es simplificar primero el exponente. El resultado será el mismo, solo que obtenido a través de una ruta diferente.
Artículos de primera necesidad
- papel o computadora
- Lápiz/bolígrafo (si usa papel)
Artículos sobre el tema. "Elevar fracciones al cuadrado"
Оцените, пожалуйста статью
Popular