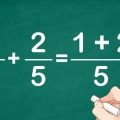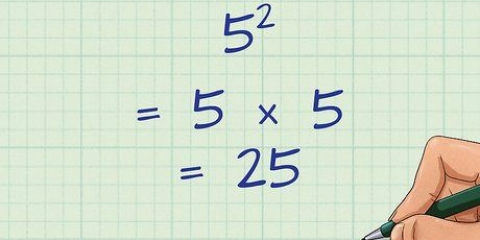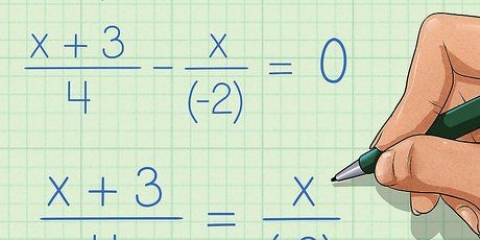18 ÷ 3 = 6, entonces 2/3 = (2x6)/(3x6)=12/18 18 ÷ 6 = 3, entonces 5/6 = (5x3)/(6x3)=15/18 18 ÷ 3 = 6, entonces 1/3 = (1x6)/(3x6)=6/18 

6/18 = (6 6)/(18 ÷ 6) = 1/3 12/18 = (12 6)/(18 ÷ 6) = 2/3 15/18 = (15 3)/(18 ÷ 3) = 5/6 La respuesta es "1/3, 2/3, 5/6" 

Esto se llama multiplicación cruzada, porque estás multiplicando números juntos en diagonal. 



Recuerda colocar siempre el producto de la multiplicación al lado de la fracción cuyo numerador usaste. 
3/5=(3x3)/(5x3)=9/15 2/3=(2x5)/(3x5)=10/15 9/15 es menos que 10/15 entonces 3/5 es menos que 2/3 

8/3 = 2 + 2/3 9/9 = 1 19/4 = 4 + 3/4 13/6 = 2 + 1/6 
1 es el más pequeño 2 + 2/3 y 2 + 1/6 (aún no sabemos cuál es más grande que el otro) 4 + 3/4 es el mayor 
2/3 = (2x2)/(3x2) = 4/6 1/6 = 1/6 4/6 es mayor que 1/6 2 + 4/6 es mayor que 2 + 1/6 2 + 2/3 es mayor que 2 + 1/6 

Ordenar fracciones por tamaño
Contenido
Si bien es fácil ordenar números enteros como 1, 3 y 8 por tamaño, no siempre es obvio con las fracciones. Si todos los denominadores son iguales, puede ordenarlos como números enteros, por ejemplo. 1/5, 3/5 y 8/5. En otros casos, puedes convertir las fracciones para que tengan el mismo denominador, sin cambiar el valor de la fracción. Esto se vuelve más fácil con la práctica y puedes usar algunos trucos útiles, tanto al comparar dos fracciones como al ordenar fracciones donde el numerador es mayor que el denominador, las fracciones impropias como 7/3.
Pasos
Método 1 de 3: Ordenar cualquier número de fracciones

1. Encuentra un denominador igual para todas las fracciones. Use uno de los siguientes métodos para encontrar un denominador, o disminuya el número de una fracción, que puede usar para volver a escribir cada fracción en la lista para facilitar la comparación. Esto es lo que llamas un común denominador, o la Mínimo común denominador si esto es lo más pequeño posible:
- Multiplica cada denominador. Por ejemplo, si está comparando 2/3, 5/6 y 1/3, multiplique estos denominadores: 3 x 6 = 18. Este es un método simple pero que a menudo da como resultado un número mucho mayor que los otros métodos, que son un poco más complicados.
- O enumere los múltiplos de cada denominador en una columna separada, hasta que se destaque un número que ocurre con más frecuencia. Por ejemplo, en 2/3, 5/6 y 1/3, tienes una lista de múltiplos de 3:3, 6, 9, 12, 15, 18. Luego una lista de múltiplos de 6: 6, 12, 18. Porque 18 ocurre en ambas listas, use ese número (también puede usar 12, pero los ejemplos a continuación asumen que usa 18).

2. Convierte cada fracción para que tengan el mismo denominador. Recuerda que si multiplicas el numerador y el denominador de una fracción por el mismo número, el valor de la fracción permanece igual. Usa esta técnica con cada fracción, una a la vez, para que cada fracción tenga el mismo denominador. Prueba esto para 2/3, 5/6 y 1/3, con el denominador 18:

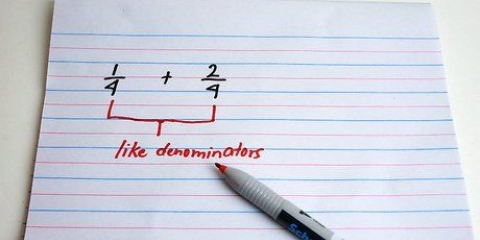
3. Ordena las fracciones por los numeradores. Ahora que todas las fracciones tienen el mismo denominador, son fáciles de comparar. Ordénalos de menor a mayor según el contador. Esto nos da la siguiente lista: 6/18, 12/18, 15/18.

4. Devuelve cada fracción a su forma original. Deje las fracciones en este orden, pero vuelva a convertirlas a la fracción original. Lo haces simplemente recordando qué fracción pertenece a cuál o dividiendo los números superior e inferior de la fracción nuevamente:
Método 2 de 3: ordenar dos fracciones con multiplicación cruzada

1. Escribe las dos fracciones una al lado de la otra. Por ejemplo, compara la fracción 3/5 y la fracción 2/3. Escriba estos uno al lado del otro: 3/5 a la izquierda y 2/3 a la derecha.

2. Multiplica el numerador de la primera fracción por el denominador de la segunda. Entonces: 3 x 3 = 9.

3. Escribe tu respuesta al lado de la primera fracción. Escribe el producto de 3 x 3 = 9, al lado de la primera fracción.

4. Multiplica el numerador de la segundo fracción con el denominador de la primero. Ahora para ver cual es la mayor, comparamos la respuesta con otra multiplicación. Multiplica estos dos números juntos. En este ejemplo (estamos comparando 3/5 y 2/3), estamos multiplicando 2 x 5.

5. Escribe la respuesta al lado de la segunda fracción. Escribe el resultado de 2 x 5 =10 al lado de la segunda fracción.

6. Comparar los valores de los resultados. Si un valor es mayor que el otro, la fracción al lado del resultado también es la más grande. Como 9 es menor que 10, 3/5 es menor que 2/3.

7. Cómo funciona esto exactamente? Lo que estás haciendo es convertir las fracciones para que ambas tengan el mismo denominador. Así que esto es lo que realmente hace la multiplicación cruzada! En realidad, omite escribir los denominadores porque en el caso de denominadores similares, solo necesita comparar los numeradores. De la siguiente manera, sin la ruta corta de la multiplicación cruzada:
Método 3 de 3: ordenar fracciones mayores que uno

1. Use este método para fracciones donde el numerador es mayor que el denominador. Si el numerador es mayor que el denominador, entonces esta fracción es mayor que 1. 8/3 es un ejemplo de esto. También puede usar esto para fracciones con el mismo numerador y denominador, como 9/9. Ambos son ejemplos de "incorrecto" fracciones.
- Todavía puedes usar los otros métodos para estas fracciones. Este método te ayudará a comprender mejor estas fracciones y puede ser un poco más rápido.

2. Convierte cualquier fracción impropia en una fracción mixta. Que sea una combinación de un número entero y una fracción. A veces puedes hacer esto fácilmente de memoria. Por ejemplo, 9/9 = 1. En los casos más complicados, usa la división larga para averiguar cuántas veces el denominador es divisible por el numerador. Cualquier resto de la división larga queda como una fracción. Por ejemplo:

3. Ordenar los números mixtos por el número entero. Ahora que ya no existen las fracciones impropias, tienes una mejor idea del tamaño de cada número. Ignora las fracciones primero y ordena cada número mixto por el entero:

4. Compara las fracciones de cada grupo si es necesario. Si tiene varios números mixtos con el mismo entero, como 2 + 2/3 y 2 + 1/6, compare la fracción de ambos números para averiguar cuál es mayor. En el ejemplo, estamos comparando 2 + 2/3 y 2 + 1/6, convirtiendo las fracciones al mismo denominador:

5. Use el resultado para ordenar aún más la lista de números mixtos. El orden de toda la lista ahora es: 1, 2 + 1/6, 2 + 2/3, 4 + 3/4.

6. Convierte los números mixtos de nuevo a las fracciones originales. Mantenga el mismo orden, pero deshaga los cambios y reescriba las fracciones como las fracciones impropias originales: 9/9, 8/3, 13/6, 19/4.
Consejos
- Al secuenciar una gran cantidad de fracciones, puede ser útil comparar pequeños grupos de 2, 3 o 4 fracciones.
- Si bien encontrar el mínimo común denominador puede ser útil, cualquier denominador común funcionará. Intente clasificar 2/3, 5/6 y 1/3 con un denominador común de 36 y vea si obtiene el mismo resultado.
- Si los numeradores son todos iguales, también puedes ordenar rápidamente las fracciones. Por ejemplo, 1/8 < 1/7 < 1/6 < 1/5. Piensa en esto como si fuera una pizza: si pasas de 1/2 a 1/8, cortas la pizza en 8 pedazos en lugar de 2 y los pedazos son más pequeños.
Artículos sobre el tema. "Ordenar fracciones por tamaño"
Оцените, пожалуйста статью
Popular