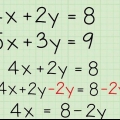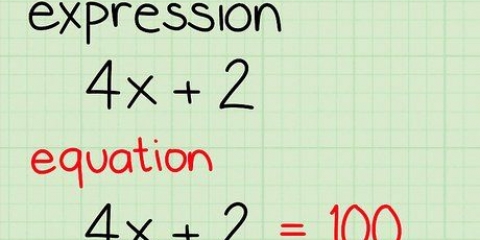La multiplicación cruzada funciona con principios algebraicos comunes. Las expresiones racionales y otras fracciones se pueden convertir en números ordinarios multiplicando los denominadores. La multiplicación cruzada es básicamente una forma conveniente y abreviada de multiplicar ambos lados de la ecuación por los denominadores de las fracciones. No lo crees? Pruébelo: verá los mismos resultados después de simplificar. 
Por ejemplo, si (x+3)/4 = x/(-2) era su expresión racional original, luego de multiplicar en cruz se vuelve igual a -2(x+3) = 4x. Esto posiblemente se puede reescribir como -2x - 6 = 4x. 
En nuestro ejemplo, es posible dividir ambos lados de la ecuación por -2, lo que nos da x+3 = -2x. Restar x de ambos lados del signo igual nos da 3 = -3x. Y finalmente, dividiendo ambos lados por -3 obtenemos -1 = x, o también x = -1. Ahora hemos encontrado x resolviendo nuestra ecuación racional. 

A veces, el mínimo común múltiplo, el número más pequeño que es divisible por cada uno de los denominadores, es inmediatamente aparente. Por ejemplo, si su expresión se parece a x/3 + 1/2 = (3x+1)/6, entonces es fácil ver que el mcm debe ser divisible por 3, 2 y 6, por lo que es igual a 6. Pero más a menudo, el LCF de una ecuación racional no está del todo claro de inmediato. En esos casos, prueba con los múltiplos del denominador más grande hasta que encuentres un número que incluya los múltiplos de los otros denominadores más pequeños. A menudo, el LCF es un producto de dos denominadores. Por ejemplo, toma la ecuación x/8 + 2/6 = (x - 3)/9, donde mcm es igual a 8*9 = 72. Si uno o más de los denominadores contiene una variable, este proceso es algo más difícil, pero ciertamente no es imposible. En esos casos, el LCF es una expresión (con variables) en la que todos los denominadores encajan completamente, no solo un número. Como ejemplo, la ecuación 5/(x-1) = 1/x + 2/(3x), donde el mcg es igual a 3x(x-1), porque es completamente divisible por cualquier denominador, dividiendo por (x- 1 ) da 3x, la división por 3x da (x-1) y la división por x da 3(x-1). 
En nuestro ejemplo, podemos multiplicar x/3 por 2/2 para obtener 2x/6 y multiplicar 1/2 por 3/3 para obtener 3/6. 3x +1/6 ya tiene un 6 (MCM) como denominador, entonces podemos multiplicarlo por 1/1 o simplemente dejarlo como está. En nuestro ejemplo con variables en los denominadores, todo el proceso es un poco más complicado. Dado que el mcc es igual a 3x(x-1), multiplicamos cualquier expresión racional por una fracción que produzca 3x(x-1) como denominador. Multiplicamos 5/(x-1) por (3x)/(3x) y esto da 5(3x)/(3x)(x-1), multiplicamos 1/x por 3(x-1)/3(x -1) y esto da 3(x-1)/3x(x-1) y multiplicamos 2/(3x) por (x-1)/(x-1) y esto finalmente da 2(x-1)/ 3x(x-1). 
En nuestro ejemplo, después de multiplicar, apostando 1 como fracción, obtenemos 2x/6 + 3/6 = (3x+1)/6. Se pueden sumar dos fracciones si tienen el mismo denominador, entonces podemos escribir esta ecuación como (2x+3)/6 = (3x+1)/6 sin cambiar su valor. Multiplica ambos lados por 6 para cancelar los denominadores, dejándonos con 2x+3 = 3x+1. Aquí resta 1 de ambos lados para obtener 2x+2 = 3x y resta 2x de ambos lados para obtener 2 = x, que también se puede escribir como x = 2. En nuestro ejemplo con variables en los denominadores, la ecuación después de multiplicar cada término por "1" igual a 5(3x)/(3x)(x-1) = 3(x-1)/3x(x-1) + 2(x-1)/3x(x-1). Multiplicar cada término por el mcm permite eliminar los denominadores, lo que nos da 5(3x) = 3(x-1) + 2(x-1). Esto se elabora aún más como 15x = 3x - 3 + 2x -2, que nuevamente se puede simplificar como 15x = x - 5. Restar x de ambos lados produce 14x = -5, lo que puede simplificar la respuesta final a x = -5/14.
Resolver ecuaciones con fracciones
Contenido
Una función racional es una fracción con una o más variables en el numerador o denominador. Una ecuación racional es cualquier ecuación que contiene al menos una expresión racional. Al igual que las ecuaciones algebraicas regulares, las expresiones racionales se pueden resolver aplicando la misma operación a ambos lados de la ecuación hasta que la variable quede aislada en un lado del signo igual. Dos métodos especiales, la multiplicación cruzada y la búsqueda del mínimo común múltiplo de los denominadores, son particularmente útiles para aislar variables y resolver ecuaciones racionales.
Pasos
Método 1 de 2: Método uno: Multiplicación cruzada

1. Si es necesario, reorganiza la ecuación para asegurarte de que haya una fracción en ambos lados del signo igual. La multiplicación cruzada es un método rápido para resolver ecuaciones racionales. Desafortunadamente, este método solo funciona para ecuaciones racionales que tienen exactamente una expresión o fracción racional en ambos lados del signo igual. Si este no es el caso en su ecuación, entonces probablemente necesite algunas operaciones algebraicas para colocar los términos en el lugar correcto. Algunas ecuaciones racionales no se pueden convertir tan fácilmente a la forma correcta. En esos casos, use los métodos que usan el mínimo común múltiplo de los denominadores.
- Por ejemplo, la ecuación (x + 3)/4 - x/(-2) = 0 se puede convertir fácilmente a la forma correcta para la multiplicación cruzada sumando x/(-2) a ambos lados de la ecuación, lo que da como resultado se ve así: (x + 3)/4 = x/(-2).
- Recuerda que los decimales y enteros se pueden convertir a fracciones dándoles como denominador 1. (x + 3)/4 - 2.5 = 5, por ejemplo se puede reescribir como (x + 3)/4 = 7.5/1, que permite aplicar la multiplicación cruzada.

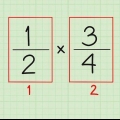
2. multiplicar en cruz. La multiplicación cruzada simplemente significa multiplicar el numerador de una fracción por el denominador de la otra y viceversa. Multiplica el numerador de la fracción a la izquierda del signo igual por la fracción a la derecha. Repite con el numerador a la derecha y el denominador de la fracción a la izquierda.

3. Haz que los dos productos sean iguales. Después de la multiplicación cruzada, te quedan dos productos. Haga que estos dos términos sean iguales y simplifíquelos para dejar los términos más simples en ambos lados de la ecuación.

4. Resolver para la variable. Usar operaciones algebraicas para encontrar el valor de la variable en la ecuación. Recuerde que si x aparece en ambos lados del signo igual, debe sumar o restar un término x para asegurarse de que solo haya términos x en un lado del signo igual.
Método 2 de 2: método dos: encontrar el mínimo común múltiplo (mcm) de los denominadores

1. Intenta ver cuándo encontrar el mínimo común múltiplo de los denominadores es obvio. El mínimo común múltiplo (MCM) de los denominadores se puede utilizar en la simplificación de ecuaciones racionales, lo que permite encontrar los valores de sus variables. Encontrar un LCF es una buena idea si la ecuación racional no se puede reescribir fácilmente en una forma en la que solo hay una fracción o expresión racional a cada lado del signo igual. Para resolver ecuaciones racionales con tres términos o más, los LCF son una herramienta útil. Pero para resolver ecuaciones racionales con solo dos términos, la multiplicación cruzada suele ser más rápida.

2. Examina el denominador de cada fracción. Encuentra el número más pequeño que es divisible por cualquier denominador. Este es el kgv de tu ecuación.

3. Multiplica cada fracción en la ecuación racional por 1. Multiplicar cualquier término por 1 puede parecer inútil, pero aquí hay un truco. 1 se puede escribir como una fracción, p. 2/2 y 3/3. Multiplica cada fracción en tu ecuación racional por 1, escribiendo 1 cada vez que el número o término se multiplica por cada denominador para representar el lcg como una fracción.

4. Simplifica y resuelve para x. Ahora que todos los términos de la ecuación racional tienen el mismo denominador, es posible eliminar los denominadores de la ecuación y resolver los numeradores. Simplemente multiplique ambos lados de la ecuación por el lcg para eliminar los denominadores de modo que solo le queden los numeradores. Ahora se ha convertido en una ecuación regular que puedes resolver para la variable aislándola en un lado del signo igual.
Consejos
- Una vez que haya encontrado el valor de la variable, verifique su respuesta insertando este valor en la ecuación original. Una vez que obtenga el valor correcto de la variable, debería poder simplificar la ecuación a un teorema simple y válido, como 1 = 1.
- Cada ecuación se puede escribir como una expresión racional; simplemente ponlo como numerador sobre el denominador 1. Entonces la ecuación x+3 se puede escribir como (x+3)/1, ambos tienen el mismo valor.
Artículos sobre el tema. "Resolver ecuaciones con fracciones"
Оцените, пожалуйста статью
Popular