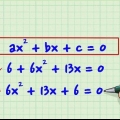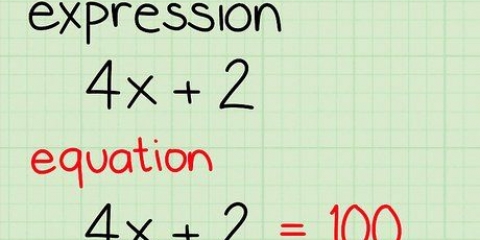Como 3x tiene un número finito de factores posibles, 3x y x, puedes escribirlos entre paréntesis: (3x +/- ? )(x +/-- ?) = 0. Luego usa un método de eliminación donde usas los factores de 4 para encontrar una combinación que dé -11x como resultado de la multiplicación. Puedes usar una combinación de 4 y 1, o 2 y 2, porque la multiplicación de ambas combinaciones de números produce 4. Tenga en cuenta que uno de los términos debe ser negativo, porque el término es -4. Prueba (3x +1)(x -4). Cuando resuelves esto obtienes - 3x -12x +x -4. Si combinas los términos -12x y x obtienes -11x, que es el término medio al que querías llegar. Ahora has factorizado esta ecuación cuadrática. Otro ejemplo; tratamos de factorizar una ecuación que no funciona: (3x-2)(x+2) = 3x +6x -2x -4. Si combinas estos términos, obtienes 3x -4x -4. Aunque el producto de -2 y 2 es igual a -4, el término medio no funciona porque estabas buscando -11x, no -4x. 

3x + 1 = 0 = 3x = -1 = 3x/3 = -1/3 x = -1/3 x - 4 = 0 x = 4 x = (-1/3, 4) 

Entonces, ambas soluciones funcionan por separado y se verifica que ambas funcionan y son correctas en dos soluciones diferentes. 



{-b +/-√ (b - 4ac)}/2 {-(-5) +/-√ ((-5) - 4(3)(-8))}/2(3) = {-(-5) +/-√ ((-5) - (-96))}/2(3) 
{-(-5) +/-√ ((-5) - (-96))}/2(3) = {5 +/-√(25 + 96)}/6 {5 +/-√(121)}/6 

(5 + 11)/6 (5 - 11)/6 
(5 + 11)/6 = 16/6 (5-11)/6 = -6/6 
16/6 = 8/3 -6/6 = -1 x = (-1, 8/3) 

2x - 12x - 9 = 0 2x - 12x = 9 
2x/2 - 12x/2 = 9/2 = x - 6x = 9/2 
-6/2 = -3 = (-3) = 9 = x - 6x + 9 = 9/2 + 9 


x = 3 +(√6)/2 x = 3 - (√6)/2)
Resolver ecuaciones cuadráticas
Contenido
Una ecuación cuadrática es una ecuación donde el mayor exponente de una variable es dos. Tres de los métodos más utilizados para resolver estas ecuaciones son: factorizar, usar la fórmula abc o dividir el cuadrado. Si quieres saber cómo dominar estos métodos, solo sigue estos pasos.
Pasos
Método 1 de 3: factorización

1. Mover todos los términos a un lado de la ecuación. El primer paso en la factorización es mover todos los términos a un lado de la ecuación, dejando x positivo. Aplicar la operación de suma o resta a los términos x, la variable x y las constantes, moviéndolos a un lado de la ecuación de esta manera, sin dejar nada en el otro lado. Así es como funciona:
- 2x - 8x - 4 = 3x - x =
- 2x +x - 8x -3x - 4 = 0
- 3x - 11x = 0

2. Factoriza la expresión. Para factorizar la expresión necesitas factorizar los factores de 3x y los factores de la constante -4 para multiplicarlos y luego sumarlos para dar el valor del término medio, -11. Así es como se hace:

3. Determinar que cada par de paréntesis es igual a cero y tratarlos como ecuaciones separadas. Esto hace que encuentres dos valores para x que hacen que la ecuación completa sea igual a cero. Ahora que has factorizado la ecuación, todo lo que queda por hacer es hacer que cada par de paréntesis sea igual a cero. Entonces puedes escribir que: 3x +1 = 0 y x - 4 = 0.

4. Resuelve cada ecuación. En una ecuación cuadrática hay dos valores dados para x. Resuelva cada ecuación por separado aislando la variable y escriba los resultados de x. Así es como funciona:

5. Compruebe x = -1/3 pulg (3x + 1)(x – 4) = 0:
Obtenemos (3[-1/3] + 1)([-1/3] – 4) ?=? 0 ..... sustituyendo:(-1 + 1)(-4 1/3) ?=? 0 ..... simplificando:(0)(-4 1/3) = 0 ..... multiplicando: entonces 0=0 ..... Sí, x = -1/3 funciona
Obtenemos (3[-1/3] + 1)([-1/3] – 4) ?=? 0 ..... sustituyendo:(-1 + 1)(-4 1/3) ?=? 0 ..... simplificando:(0)(-4 1/3) = 0 ..... multiplicando: entonces 0=0 ..... Sí, x = -1/3 funciona

6. Compruebe x = 4 pulgadas (3x + 1)(x - 4) = 0:
Obtenemos (3[4] + 1)([4] – 4) ?=? 0..... sustituyendo:(13)(4 – 4) ?=? 0 ..... atenuando:(13)(0) = 0 ..... multiplicando:0=0 ..... Sí, x = 4 obras
Obtenemos (3[4] + 1)([4] – 4) ?=? 0..... sustituyendo:(13)(4 – 4) ?=? 0 ..... atenuando:(13)(0) = 0 ..... multiplicando:0=0 ..... Sí, x = 4 obras
Método 2 de 3: aplicar la fórmula Abc

1. Mover todos los términos a un lado de la ecuación y fusionar los términos semejantes. Mover todos los términos a un lado del signo igual, manteniendo el término x positivo. Escriba los términos en orden descendente de magnitud, de modo que x sea lo primero, seguido de x, luego la constante. Así es como se hace:
- 4x - 5x - 13 =x -5
- 4x - x - 5x - 13 +5 = 0
- 3x - 5x - 8 = 0

2. Escriba la fórmula abc. Esto es: {-b +/-√ (b - 4ac)}/2a

3. Determinar los valores de a, b y c en la ecuación cuadrática. La variable a es el coeficiente de x, B es el coeficiente de x y C es la constante. Para la ecuación 3x -5x - 8 = 0, a = 3, b = -5 y c = -8. Escribe esto.

4. Sustituye los valores de a, b y c en la ecuación. Ahora que conoce los valores de las tres variables, simplemente puede introducirlos en la ecuación como mostramos aquí:

5. Calcular. Después de completar los números, resuelve el problema más a fondo. A continuación puede leer cómo va más allá:

6. Simplifica la raíz cuadrada. Si el número debajo del signo radical es un cuadrado perfecto o también un número cuadrado, entonces obtienes un número entero con la raíz cuadrada. En otros casos, simplifica la raíz cuadrada tanto como sea posible. Si el número es negativo y está seguro de que esa es la intención, entonces la raíz cuadrada del número será menos simple. En este ejemplo, √(121) = 11. Entonces puedes escribir que x =(5 +/- 11)/6.

7. Resolver para los números positivos y negativos. Una vez que te hayas deshecho de la raíz cuadrada, puedes continuar hasta que encuentres las respuestas negativa y positiva para x. Ahora que tienes (5 +/- 11)/6, puedes escribir las dos posibilidades:

8. Resuelve las respuestas positivas y negativas. Calcula más:

9. Simplificar. Para simplificar, divida las respuestas por el número más grande divisible por el numerador y el denominador. Entonces divide la primera fracción por 2 y la segunda por 6 y has resuelto x.
Método 3 de 3: dividir el cuadrado

1. Mover todos los términos a un lado de la ecuación. Asegúrate que a de x es positivo. Así es como se hace:
- 2x - 9 = 12x =
- 2x - 12x - 9 = 0
- En esta ecuación, a igual a 2, B es -12, y C es -9.

2. Mueve la constante C al otro lado. La constante es el valor numérico sin variable. Muévelo al lado derecho de la ecuación:

3. Divide los dos lados por el coeficiente de la a o x término. Si x no tiene un término delante y tiene un coeficiente con el valor 1, puede omitir este paso. En este caso, necesitas dividir todos los términos por 2, así:

4. Parte B por dos, elevarlo al cuadrado y sumar los resultados a ambos lados del signo es.ElB en este ejemplo es -6. Así es como se hace esto:

5. Simplifica ambos lados. Factoriza los términos de la izquierda para obtener (x-3)(x-3), o (x-3). Sume los términos a la derecha para obtener 9/2 + 9, o 9/2 + 18/2, que suma 27/2.

6. Encuentra la raíz cuadrada de ambos lados. La raíz cuadrada de (x-3) es simplemente (x-3). También puedes escribir la raíz cuadrada de 27/2 como ±√(27/2). Por lo tanto, x - 3 = ±√(27/2).

7. Simplifica la raíz cuadrada y resuelve para x. Para simplificar ±√(27/2), busca un cuadrado perfecto o número cuadrado con los números 27 o 2 o en sus factores. El número cuadrado 9 se encuentra en 27, porque 9 x 3 = 27. Para eliminar 9 de la raíz, escríbelo como una raíz separada y simplifica a 3, la raíz cuadrada de 9. Deja √3 en el numerador de la fracción porque no se puede separar como factor de 27, y haz 2 en el denominador. Luego mueve la constante 3 del lado izquierdo de la ecuación al lado derecho y escribe tus dos soluciones para x:
Consejos
- Como puedes ver, el signo radical no ha desaparecido por completo. Por lo tanto, los términos del numerador no se fusionan (no son términos iguales). Entonces no tiene sentido dividir los menos y los más. En cambio, al dividir, nos aseguramos de que todo factor común desaparezca, pero "SOLO" si el factor es igual para ambas constantes, "Y" el coeficiente de la raiz cuadrada.
Artículos sobre el tema. "Resolver ecuaciones cuadráticas"
Оцените, пожалуйста статью
Popular