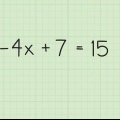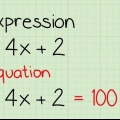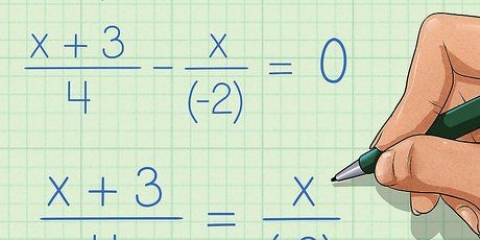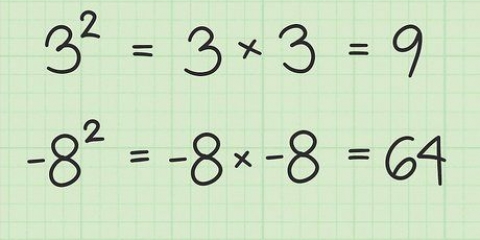4(x+3) + 9 - 5 = 32 
4x + 12 + 9 - 5 = 32 
4x+21-5 = 32 4x+16 = 32 4x + 16 - 16 = 32 - 16 4x = 16 
4x/4 = 16/4 x = 4 
2(x+3)+ 9 - 5 = 32 2(4+3)+ 9 - 5 = 32 2(7) + 9 - 5 = 32 4(7) + 9 - 5 = 32 28 + 9 - 5 = 32 37 - 5 = 32 32 = 32 

2x+12-12 = 44-12 2x = 32 
(2x)/2 = 32/2 X = 16 

2x + 12 = 44 2 x (4) + 12 = 44 2 x 16 + 12 = 44 32 + 12 = 44 44 = 44 

(x + 3)/6 = 2/3 6x2 = 12 (x + 3) x 3 = 3x + 9 3x + 9 = 12 
3x + 9 - 9 = 12 - 9 3x = 3 

(x + 3)/6 = 2/3 (1 + 3)/6 = 2/3 4/6 = 2/3 2/3 = 2/3 

√(2x+9) - 5 + 5 = 0 + 5 √(2x+9) = 5 
(√(2x+9)) = 5 2x + 9 = 25 
2x + 9 - 9 = 25 - 9 2x = 16 

√(2x+9) - 5 = 0 √(2(8)+9) - 5 = 0 √(16+9) - 5 = 0 √(25) - 5 = 0 5 - 5 = 0 

|4x +2| - 6 = 8 |4x +2| - 6 + 6 = 8 + 6 |4x +2| = 14 
4x + 2 = 14 4x + 2 - 2 = 14 -2 4x = 12 x = 3 
4x + 2 = -14 4x + 2 - 2 = -14 - 2 4x = -16 4x/4 = -16/4 X = -4 
(Para x = 3): |4x +2| - 6 = 8 |4(3) +2| - 6 = 8 |12 +2| - 6 = 8 |14| - 6 = 8 14 - 6 = 8 8 = 8 (para x = -4): |4x +2| - 6 = 8 |4(-4) +2| - 6 = 8 |-16 +2| - 6 = 8 |-14| - 6 = 8 14 - 6 = 8 8 = 8
Resolver x en una ecuación
Contenido
Hay varias formas de resolver x en una ecuación, ya sea que esté trabajando con exponentes y raíces o simplemente necesite dividir o multiplicar. Independientemente del método que utilice, siempre debe encontrar una forma de aislar x de un lado de la ecuación para que pueda calcular el valor. Así es como se hace:
Pasos
Método 1 de 5: usar una ecuación lineal ordinaria

1. Escribe el problema. Aquí está la tarea:
- 2(x+3) + 9 - 5 = 32

2. Calcula el exponente. Recuerde el orden de las operaciones: HMVDOA, que significa Paréntesis, Exponenciación, División/Multiplicación, Suma/Resta. En este caso, no puedes averiguar lo que está entre paréntesis primero porque la x le pertenece, así que empiezas con la potencia, 2. 2 = 4

3. Calcula la multiplicación. Multiplica 4 por (x+3). Así es cómo:

4. Ahora calcula la suma y la resta. Solo suma o resta los números restantes. Así es cómo:

5. Aislar la variable. Haces esto dividiendo ambos lados de la ecuación por 4 para encontrar x. 4x/4 = x y 16/4 = 4, entonces x = 4.

6. Comprueba tu cálculo. Sustituye x = 4 de nuevo en la ecuación original para asegurarte de que sea correcta. Así es cómo:
Método 2 de 5: con exponenciación

1. Escribe el problema. Supongamos que está trabajando en un problema en el que el término x también contiene un exponente:
- 2x + 12 = 44

2. Aislar el término con el exponente. Lo primero que debes hacer ahora es combinar términos semejantes para que todas las constantes estén en el lado derecho de la ecuación mientras que el término con el exponente esté en el lado izquierdo. Solo resta 12 de ambos lados. Así es cómo:

3. Aislar la variable con el exponente, dividiendo ambos lados por el coeficiente del término x. En este caso, 2 es el coeficiente x, lo que significa que ambos lados deben dividirse por 2 para eliminarlo. Así es cómo:

4. Saca la raíz cuadrada de cada lado de la ecuación. Al calcular la raíz cuadrada de x, te queda x a la izquierda y la raíz cuadrada de 16.4, a la derecha. Entonces, x = 4.

5. Comprueba tu cálculo. Sustituye x = 4 de nuevo en la ecuación original para asegurarte de que sea correcta. Así es cómo:
Método 3 de 5: usar fracciones

1. Escribe el problema. Supongamos que está lidiando con el siguiente problema:
- (x + 3)/6 = 2/3

2. multiplicar en cruz. Para multiplicar en cruz, multiplica el denominador de cada fracción por el numerador de la otra fracción. Entonces, multiplica 6 (el primer denominador) por 2 (el segundo numerador), para obtener 12 en el lado derecho de la ecuación.Luego multiplica 3 (el segundo denominador) por x + 3 (el primer numerador), para obtener 3 x + 9 a la izquierda de la ecuación. Así es como se verá:

3. Combinar términos semejantes. Combine las constantes en la ecuación restando 9 de ambos lados de la ecuación. Esto es lo que debe hacer:

4. Aislar x dividiendo cada término por el coeficiente x. Simplemente divida 3x y 9 por 3, el coeficiente de x, y resuelva para x. 3x/3 = x y 3/3 = 1, por lo que te queda x = 1.

5. Comprueba tu cálculo. Para verificar su trabajo, sustituya x nuevamente en la ecuación original para asegurarse de que sea correcta. Esto es lo que debe hacer:
Método 4 de 5: usar caracteres raíz

1. Escribe el problema. Supongamos que resuelve x en el siguiente problema:
- √(2x+9) - 5 = 0

2. Aislar la raíz cuadrada. Debe aislar la parte de la raíz cuadrada de la ecuación a la izquierda de la ecuación antes de poder continuar. Entonces sumas 5 a ambos lados de la ecuación. Así es cómo:

3. Dibujar la raíz cuadrada de ambos lados. Así como divides ambos lados de una ecuación por el coeficiente multiplicado por x, también debes sacar la raíz cuadrada de ambos lados de una ecuación si x está por debajo del signo radical. Esto elimina el radical de la ecuación. Así es como se hace esto:

4. Combinar términos semejantes. Combine términos iguales restando 9 de ambos lados de la ecuación para que todas las constantes estén a la derecha, mientras que x permanece a la izquierda. Esto es lo que debe hacer:

5. Aislar la variable. Lo último que debe hacer para resolver x es aislar la variable dividiendo ambos lados de la ecuación por 2, el coeficiente del término x. 2x/2 = x y 16/2 = 8, por lo que te queda x = 8.

6. Comprueba tu cálculo. Ingrese 8 en la ecuación nuevamente para x para verificar que su cálculo sea correcto:
Método 5 de 5: usa el valor absoluto

1. Escribe el problema. Supongamos que está tratando de resolver x en el siguiente problema:
- |4x +2| - 6 = 8

2. Aislar el valor absoluto. Lo primero que hay que hacer es combinar términos semejantes y aislar el valor absoluto. En este caso, puedes hacerlo sumando 6 a ambos lados de la ecuación. Así es cómo:

3. Elimina el valor absoluto y resuelve la ecuación. Este es el primer y más fácil paso. Ahora tienes que resolver x dos veces, cada vez que trabajes con un valor absoluto. He aquí cómo hacer esto la primera vez:

4. Elimina el valor absoluto y cambia el signo de los términos al otro lado del signo igual antes de continuar resolviendo. Ahora haz esto de nuevo, esta vez haciendo que la parte izquierda de la ecuación sea igual a -14 en lugar de 14. Así es cómo:

5. Comprueba tu cálculo. Ahora que sabe que x = (3, -4), simplemente sustituya ambos números en la ecuación para asegurarse de que sea correcto. Así es cómo:
Consejos
- Para comprobar tu trabajo, vuelve a introducir el valor de x en la ecuación original y resuélvelo.
- Las raíces son otra forma de representar exponentes.La raíz cuadrada de x = x^1/2.
Artículos sobre el tema. "Resolver x en una ecuación"
Оцените, пожалуйста статью
Popular