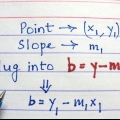El constante B se define como la `intersección con el eje y` Este es el punto en el que la línea se cruza con el eje y.
Ambos X Si y son variables. Por ejemplo, puede especificar un valor de X Resuelve si tu y saber, así como los valores metro y B. El X sin embargo, nunca es solo un valor: el valor cambia a medida que se mueve hacia arriba o hacia abajo en el gráfico.

Por ejemplo, tomamos la ecuación y = 1/4x + 5. Desde el último dígito B es que sabemos que B es igual a 5. Sube 5 puntos en el eje y y marca el punto. Aquí es donde su línea recta cruzará el eje y.

El primer número (el numerador) es el aumento de y sobre x. Esto es lo lejos que sube la línea (se mueve verticalmente).
El segundo número (el denominador) es el X en y sobre x. Esto es lo lejos que se mueve la línea (se desplaza horizontalmente).
Por ejemplo:
Una pendiente de 4/1 aumenta 4 puntos por cada desplazamiento horizontal de 1 punto. Una pendiente de -2/1 cae 2 puntos por cada desplazamiento horizontal de 1 punto. Una pendiente de 1/5 aumenta 1 punto por cada desplazamiento horizontal de 5 puntos. 
Por ejemplo, en el gráfico anterior puedes ver que por cada punto que la línea aumenta, se desplaza cuatro puntos a la derecha. Eso es porque la pendiente de la recta es ¼ (y/x). Continúa extendiendo la línea a lo largo de ambos lados usando y sobre x. Mientras que las pendientes positivas suben, las pendientes negativas bajan. Una pendiente de -1/4, por ejemplo, baja un punto por cada cuatro puntos que se desplaza hacia la derecha. 
Dibujar una ecuación lineal
No sé dibujar una ecuación lineal sin calculadora? Afortunadamente, graficar una ecuación lineal es bastante simple! Solo necesita saber algunas cosas sobre su ecuación y está listo para comenzar. Empecemos!
Pasos

1. Asegúrate de que sea una ecuación lineal de la forma y = mx + b. Esto se llama la intersección y, y es probablemente el gráfico más simple de una ecuación lineal. Los valores en la ecuación no tienen que ser números enteros. A menudo ves una ecuación como: y = 1/4x + 5, donde 1/4 es igual metro y 5 en B.
- El constante metro se llama la `pendiente`, o la `pendiente`. La colina se define como un cambio en y en relación con el cambio de X.




2. dibujar el numero B en el eje y. El constante B siempre es un numero racional. cual es el numero B también, encuentre su equivalente en el eje y y dibuje su número en ese punto en el eje vertical.


3. Muevete metro estar en una fractura. El número X a menudo ya es una fracción, por lo que no es necesario convertirla. Pero si no, conviértalo simplemente cambiando el valor de metro como numerador y 1 como denominador.



4. Comience a extender la línea desde B utilizando la conocida pendiente. Comience en el valor de B: sabemos que la ecuación pasa por este punto. Extiende la línea usando la pendiente para determinar los siguientes puntos de la ecuación.

5. Continúe extendiendo la línea (usando una regla y usando la pendiente metro como guía. Extienda la línea a lo largo de ambos lados (hasta el infinito), y habrá terminado de graficar la línea. Bastante fácil, ¿no??
Artículos sobre el tema. "Dibujar una ecuación lineal"
Оцените, пожалуйста статью
Popular