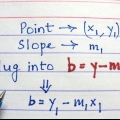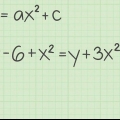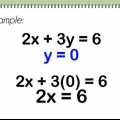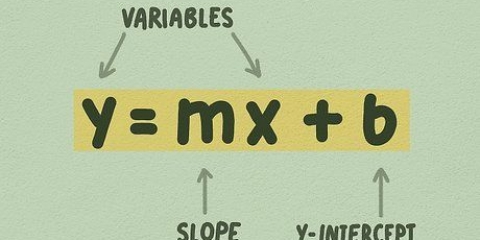Encuentra la intersección de una ecuación con el eje Y

Contenido

Pasos
Consejos

La intersección y de una ecuación es el punto donde la gráfica de una ecuación se cruza con el eje y. Hay varias formas de encontrar esta intersección, dependiendo de la información proporcionada al comienzo de su comando.

Pasos

Método 1 de 3: Encontrar la intersección con el eje y, usando la pendiente

Imagen titulada Find the Y Intercept Step 1

1. Tenga en cuenta la pendiente. La pendiente de `y sobre x` es un solo número que indica la pendiente de una línea. Este tipo de problema también le da la (x, y)-coordenada de un punto en la grafica. Si no tiene estos dos detalles, continúe con los otros métodos a continuación.

Ejemplo 1: Una recta con pendiente 2 pasa por el punto (-3.4). Determine la intersección con el eje y de esta línea siguiendo los pasos a continuación.

Imagen titulada Encuentra la intercepción Y Paso 2

2. Aprende la forma habitual de una ecuación lineal. Cualquier línea recta se puede escribir como y = mx + b. Cuando la ecuación está en esta forma, es metro la pendiente y la constante B la intersección con el eje y.

Imagen titulada Encuentra la intercepción Y Paso 3

3. Sustituye la pendiente en esta ecuación. Escriba la ecuación lineal, pero en lugar de metro usas la pendiente de tu linea.

Ejemplo 1 (continuación):y = metrox + segundo
metro = pendiente = 2
y = 2x + segundo

Imagen titulada Find the Y Intercept Step 4

4. Reemplace x e y con las coordenadas del punto. Si tienes las coordenadas de un punto en la línea, puedes X y y-sustituir las coordenadas por las X y y en tu ecuacion lineal. Haga esto para la comparación de su tarea.

Ejemplo 1 (continuación): El punto (3,4) está en esta línea. en este punto, x = 3 y y = 4.
Sustituye estos valores en y = 2X +B:
4 = 2(3) + segundo

Imagen titulada Encuentra la intercepción Y Paso 5

5. Resolver B. No lo olvide, B es la intersección con el eje y de la recta. Ahora B es la única variable en la ecuación, reorganizar la ecuación para resolver esta variable y encontrar la respuesta.

Ejemplo 1 (continuación):4 = 2(3) + segundo
4 = 6 + segundo
4 - 6 = segundo
-2 = segundo
La intersección de esta línea con el eje y es -2.

Imagen titulada Encuentra la intercepción Y Paso 6

6. Escribe esto como una coordenada. La intersección con el eje y es el punto donde la línea se cruza con el eje y. Dado que el eje y pasa por el punto x = 0, la coordenada x de la intersección con el eje y siempre es 0.

Ejemplo 1 (continuación): La intersección con el eje y está en y = -2, por lo que el punto de coordenadas es (0, -2).

Método 2 de 3: usar dos puntos

Imagen titulada Encuentra la intercepción Y Paso 7

1. Tenga en cuenta las coordenadas de ambos puntos. Este método se ocupa de problemas en los que sólo se dan dos puntos en una línea recta. Escribe cada coordenada en la forma (x,y).

Imagen titulada Encuentra la intercepción Y Paso 8

2. Ejemplo 2: Una recta pasa por los puntos (1, 2) y (3, -4). Determine la intersección con el eje y de esta línea siguiendo los pasos a continuación.

Imagen titulada Encuentra la intercepción Y Paso 9

3. Calcular los valores de x e y. La pendiente o pendiente es una medida de cuánto se mueve la recta en dirección vertical por cada paso en dirección horizontal. Puede conocer esto como `y sobre x` (

\frac{y}{X}

${frac{y}{x}}$ ). He aquí cómo determinar estos valores usando dos puntos:

El cambio de `y` es el cambio en la dirección vertical, o la diferencia entre la y-valores de los dos puntos.

El cambio de `x` es el cambio en la dirección horizontal, o la diferencia entre el X-valores de los dos puntos.

Ejemplo 2 (continuación): Los valores de y de los dos puntos son 2 y -4, por lo que la recta crece en dirección vertical con (-4) - (2) = -6.
Los valores de x de los dos puntos (en el mismo orden) son 1 y 3, por lo que la línea aumenta horizontalmente en 3 - 1 = 2.

Imagen titulada Encuentra el paso de intersección Y 10

4. Divide y por x para determinar la pendiente. Ahora que conoce estos dos valores, puede usarlos en `

\frac{y}{X}

${frac{y}{x}}$ ` para determinar la pendiente de la recta.

Ejemplo 2 (continuación):

s yo O pags mi = \frac{y}{X} = - 6 2 =

$pendiente={frac{y}{x}}={frac{-6}{2}}=$ -3.

Imagen titulada Encuentra el paso de intersección Y 11

5. Echa otro vistazo a la forma estándar de una ecuación lineal. Puedes describir una línea recta con la fórmula y = mx + b, por lo cual metro la pendiente es y B la intersección con el eje y. Ahora que tenemos la pendiente metro y un punto (x,y), podemos usar esta ecuación para encontrar B resolver (la intersección con el eje y).

Imagen titulada Encuentra la intercepción Y Paso 12

6. Completa la pendiente y el punto en la ecuación. Toma la ecuación en forma estándar y reemplaza metro por la pendiente que calculaste. Reemplazar las variables X y y por las coordenadas de un solo punto en la línea. No importa qué punto uses.

Ejemplo 2 (continuación): y = mx + b
Pendiente = m = -3, entonces y = -3x + b
La recta pasa por un punto con coordenadas (x,y) (1,2), por lo que 2 = -3(1) + segundo.

Imagen titulada Encuentra el paso de intersección Y 13

7. Resolver para b. Ahora la única variable que queda en la ecuación es B, la intersección con el eje y. Reordenar la ecuación para que B en un lado de la ecuación, y tienes tu respuesta. Recuerde que la intersección con el eje y siempre tiene una coordenada x de 0.

Ejemplo 2 (continuación): 2 = -3(1) + segundo
2 = -3 + segundo
5 = segundo
La intersección con el eje y es (0.5).

Método 3 de 3: usar una ecuación

Imagen titulada Encuentra el paso de intersección Y 14

1. Escriba la ecuación de la recta. Si tienes la ecuación de la línea, puedes determinar la intersección con el eje y con un poco de álgebra.

Ejemplo 3: ¿Cuál es la intersección con el eje y de la recta x + 4y = 16?
Nota: el ejemplo 3 es una línea recta. Consulte el final de esta sección para ver un ejemplo de una ecuación cuadrática (usando una variable elevada a la potencia de 2).

Imagen titulada Encuentra el paso de intersección Y 15

2. Sustituye 0 por x. El eje y es una línea vertical a través de x = 0. Esto significa que cualquier punto en el eje y tiene una coordenada x de 0, incluida la intersección de la línea con el eje y. Ingrese 0 para x en la ecuación.

Ejemplo 3 (continuación): x + 4y = 16
x = 0
0 + 4y = 16
4 años = 16

Imagen titulada Encuentra el paso de intersección Y 16

3. Resolver para y. La respuesta es la intersección de la recta con el eje y.

Ejemplo 3 (continuación): 4 años = 16

4 y 4 = \frac{dieciséis}{4}

${frac{4y}{4}}={frac{16}{4}}$
y = 4.
La intersección de la línea con el eje y es 4.

Imagen titulada Encuentra el paso de intersección Y 17

4. Confirme esto dibujando un gráfico (opcional). Comprueba tu respuesta graficando la ecuación con la mayor precisión posible. El punto donde la recta pasa por el eje y es la intersección con el eje y.

Imagen titulada Encuentra el paso de intersección Y 18

5. Encuentra la intersección con el eje y de una ecuación cuadrática. Una ecuación cuadrática tiene una variable (x o y) elevada a la segunda potencia. Usando la misma sustitución, puede resolver para y, pero dado que la ecuación cuadrática es una curva, puede intersecar el eje y en 0, 1 o 2 puntos. Esto significa que terminará con 0, 1 o 2 respuestas.

Ejemplo 4: Para encontrar la intersección de

y 2 = X + 1

$y^{2}=x+1$ con el eje y, sustituyes x = 0 y resolver la ecuación cuadrática.
En este caso podemos

y 2 = 0 + 1

$y^{2}=0+1$ resolver sacando la raiz cuadrada de ambos lados. Recuerda que obtienes dos respuestas al sacar una raíz cuadrada: una respuesta negativa y una positiva.

\sqrt{y} 2 = \sqrt{1}

${sqrt{y^{2}}}={sqrt{1}}$
y = 1 o y = -1. Ambos son intersección con el eje y de esta curva.

Consejos

Algunos países utilizan un C o cualquier otra variable para B en la ecuacion y = mx + b. Su significado, sin embargo, sigue siendo el mismo; es solo una notación diferente.
Para ecuaciones más complicadas, puede usar los términos con y aislar en un lado de la ecuación.
Al calcular la pendiente entre dos puntos, puede X y y-resta las coordenadas en cualquier orden, siempre que coloque el punto en el mismo orden para y y x. Por ejemplo, la pendiente entre (1, 12) y (3, 7) se puede calcular de dos formas diferentes:

Segundo punto – primer punto: $7 - 12 3 - 1 = - 5 2 = - 2.5$ ${frac{7-12}{3-1}}={frac{-5}{2}}=-2,5$
Primer punto – segundo punto: $12 - 7 1 - 3 = 5 - 2 = - 2.5$ ${frac{12-7}{1-3}}={frac{5}{-2}}=-2,5$