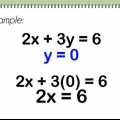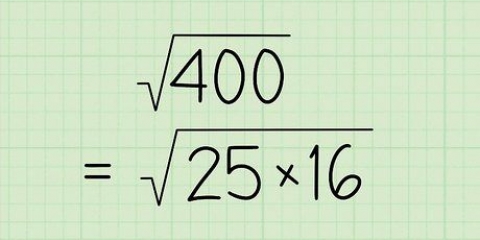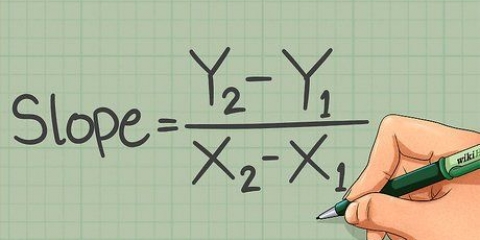Ejemplo: lo sabemos  y
y  , y por lo tanto
, y por lo tanto  .
. 
Ejemplo:
teléfono  en cada lado:
en cada lado: 
Resta 3 de cada lado: 
Divide cada lado por 3:  .
.
Ejemplo: y
y 



Ejemplo: y
y 



Esta es la misma respuesta que se obtuvo anteriormente. no cometimos ningun error. 
Ejemplo: y
y 
Las dos rectas se cortan en el punto (3.6). 
Si las dos rectas son paralelas no se cortan . Los términos x se pueden eliminar y su ecuación se puede simplificar a una ecuación inválida (como  ). Nota aquí`las lineas no se cruzan o no es una solución válida` si respondes.
). Nota aquí`las lineas no se cruzan o no es una solución válida` si respondes. Si las dos ecuaciones describen la misma línea, entonces se `intersecan` en todas partes. Puede eliminar los términos x y simplificar su ecuación a una ecuación válida (como  ). anote `las dos lineas son iguales` como respuesta.
). anote `las dos lineas son iguales` como respuesta. 

Ejemplo: Encuentre la intersección de  y
y  .
. Reescribe la ecuación cuadrática en términos de y:  y
y  .
.Este ejemplo tiene una ecuación cuadrática y una ecuación lineal. Los problemas con dos ecuaciones cuadráticas se resuelven de la misma manera. 
Ejemplo: y
y 


Ejemplo:
Resta x de cada lado: 
Resta 7 de cada lado: 

Ejemplo:
El propósito de factorizar es determinar los dos factores multiplicados juntos para producir esta ecuación. Empezando por el primer término, sabemos que  se puede dividir en x, y x. Escribe (x )(x ) = 0 para mostrar esto.
se puede dividir en x, y x. Escribe (x )(x ) = 0 para mostrar esto. El último término es -6. Escribe cada par de factores que multiplicados dan -6 como el producto:  ,
,  ,
,  , y
, y  .
. El término medio es x (que puedes escribir como 1x). Sume cada par de factores para obtener 1 como respuesta. El par correcto de factores es  , porque
, porque  .
. Complete los espacios en blanco en su respuesta con estos pocos factores:  .
. 
Ejemplo (factor): Terminamos con la ecuación  . Si ambos factores entre paréntesis son iguales a 0, entonces la ecuación es verdadera. La única solución es
. Si ambos factores entre paréntesis son iguales a 0, entonces la ecuación es verdadera. La única solución es  →
→  . La otra solución es
. La otra solución es  →
→  .
. Ejemplo (ecuación cuadrática o cuadrado divisor): si usa uno de estos métodos para resolver la ecuación, aparecerá una raíz cuadrada. Por ejemplo, nuestra ecuación se convierte en  . Recuerda que puedes simplificar una raíz cuadrada a dos soluciones diferentes:
. Recuerda que puedes simplificar una raíz cuadrada a dos soluciones diferentes:  , y
, y . Escribe dos ecuaciones, una para cada posibilidad, y resuelve x para cada una de ellas.
. Escribe dos ecuaciones, una para cada posibilidad, y resuelve x para cada una de ellas. 
Una solución: Los problemas se pueden dividir en dos factores idénticos ((x-1)(x-1) = 0). Introducida en la fórmula cuadrática, la raíz cuadrada se convierte en  . Solo necesitas resolver una ecuación.
. Solo necesitas resolver una ecuación. No hay una solución real: No hay factores que cumplan con los requisitos (listado a mediano plazo). Ingresado en la fórmula cuadrática, obtienes un número negativo debajo del radical (como  ). Escribe `sin solución` como respuesta.
). Escribe `sin solución` como respuesta. 
Ejemplo: Hemos encontrado dos soluciones,  y
y  . Una de nuestras rectas tiene la ecuación
. Una de nuestras rectas tiene la ecuación  . sustituir
. sustituir  y
y  , y resuelve cada ecuación para que obtengas
, y resuelve cada ecuación para que obtengas  y
y  si obtienes una respuesta.
si obtienes una respuesta. 
Ejemplo: Cuando nosotros  entrada, obtenemos
entrada, obtenemos  , de modo que un punto de intersección es igual a (2, 9). Hacemos lo mismo para la segunda solución, y esto nos da el punto de intersección (-3, 4) sobre.
, de modo que un punto de intersección es igual a (2, 9). Hacemos lo mismo para la segunda solución, y esto nos da el punto de intersección (-3, 4) sobre.
Calcular la intersección de dos rectas
Contenido
Cuando las líneas rectas se cruzan en un gráfico bidimensional, lo hacen en un solo punto, indicado por las coordenadas x e y. Como ambas rectas pasan por ese punto, sabes que las coordenadas x e y deben satisfacer ambas ecuaciones. Con algunas técnicas adicionales, puede encontrar las intersecciones de parábolas y otras curvas cuadráticas, usando la misma lógica.
Pasos
Método 1 de 2: Determinar la intersección entre dos líneas rectas

1. Escribe la ecuación de cualquier recta con y a la izquierda. Si es necesario, modifique la ecuación para que y quede aislado en un lado del signo igual. Si la ecuación se escribe con f(x) o g(x) en lugar de y, separe ese término. Recuerda que puedes eliminar términos realizando la misma operación en ambos lados.
- ¿Se desconocen las ecuaciones?, luego determinalo en base a la información dada.
- Ejemplo: Supongamos que tiene dos líneas
y
. Para separar y en la segunda ecuación, suma 12 a cada lado:

2. Asegúrate de que los lados derechos de las ecuaciones sean iguales. Estamos buscando un punto donde las dos líneas tengan los mismos valores de x e y; este es el punto donde las líneas se cruzan. Ambas ecuaciones tienen solo una y a la izquierda, por lo que sabemos que los lados derechos son iguales entre sí. Escribe una nueva ecuación que muestre esto.
 y
y  , y por lo tanto
, y por lo tanto  .
.
3. Resolver x en la ecuación. La nueva ecuación tiene una sola variable, x. Resuelve esto con álgebra, realizando la misma operación en ambos lados. Encuentre los términos x de cada lado de la ecuación y colóquelos en la forma x = __ (si no es posible, continúe leyendo al final de esta sección).

 en cada lado:
en cada lado:

 .
.
4. Usa este valor de x para resolver y. Elige la ecuación de cada recta. Reemplaza cada x en la ecuación con la respuesta que encontraste. Ahora resuelve para y.
 y
y 



5. Revisa tu trabajo. Es aconsejable introducir su valor de x en la otra ecuación para ver si obtiene el mismo resultado. Si obtiene otra solución para y, regrese y verifique que no haya errores en su trabajo.
 y
y 




6. Escribe las coordenadas x e y de la intersección. Ahora ha resuelto el valor x y el valor y de la intersección de las dos líneas. Escribe el punto como una coordenada, con el valor x como el primer número.
 y
y 

7. Procesar resultados inusuales. Algunas ecuaciones hacen que sea imposible resolver x. Esto no significa necesariamente que cometiste un error. Hay dos formas en las que un par de líneas pueden conducir a una solución especial:
 ). Nota aquí`las lineas no se cruzan o no es una solución válida` si respondes.
). Nota aquí`las lineas no se cruzan o no es una solución válida` si respondes. ). anote `las dos lineas son iguales` como respuesta.
). anote `las dos lineas son iguales` como respuesta.Método 2 de 2: Problemas con ecuaciones cuadráticas

1. Aprende a reconocer ecuaciones cuadráticas. En una ecuación cuadrática, hay una o más variables en forma cuadrática ( o
o  ), y no hay poderes superiores. Las líneas representadas por ecuaciones son curvas y, por lo tanto, pueden cortar una línea recta en 0, 1 o 2 puntos. En esta parte, aprenderá cómo encontrar las intersecciones de dicho problema.
), y no hay poderes superiores. Las líneas representadas por ecuaciones son curvas y, por lo tanto, pueden cortar una línea recta en 0, 1 o 2 puntos. En esta parte, aprenderá cómo encontrar las intersecciones de dicho problema.
 o
o  ), y no hay poderes superiores. Las líneas representadas por ecuaciones son curvas y, por lo tanto, pueden cortar una línea recta en 0, 1 o 2 puntos. En esta parte, aprenderá cómo encontrar las intersecciones de dicho problema.
), y no hay poderes superiores. Las líneas representadas por ecuaciones son curvas y, por lo tanto, pueden cortar una línea recta en 0, 1 o 2 puntos. En esta parte, aprenderá cómo encontrar las intersecciones de dicho problema. - Resuelve ecuaciones dentro de paréntesis para ver si son cuadráticas. Por ejemplo,
es cuadrático, porque puedes ponerlo fuera de paréntesis si
- Tener ecuaciones de un círculo o una elipse ambos a
como un
término. Si encuentra estos casos especiales difíciles, siga leyendo en los Consejos al final de este artículo.

2. Escribe las ecuaciones en términos de y. Si es necesario, reescribe cada ecuación para que y esté en un lado.
 y
y  .
. y
y  .
.
3. Combina las dos ecuaciones para eliminar la y. Si ha hecho que ambas ecuaciones sean iguales a y, entonces sabe que las dos ecuaciones sin y son iguales entre sí.
 y
y 


4. Reorganizar la nueva ecuación para que un lado sea igual a cero. Use métodos matemáticos estándar para obtener todos los términos en un lado de la ecuación. Esta es la configuración requerida de los problemas para poder resolverlos en el siguiente paso.




5.Resolver la ecuación cuadrática. Si tienes un lado igual a cero, hay tres formas de resolver la ecuación cuadrática. Todos prefieren un método diferente. Puedes leer más sobre la fórmula cuadrática de `dividir el cuadrado`, o puedes seguir este ejemplo más adelante factorizar método:

 se puede dividir en x, y x. Escribe (x )(x ) = 0 para mostrar esto.
se puede dividir en x, y x. Escribe (x )(x ) = 0 para mostrar esto. ,
,  ,
,  , y
, y  .
. , porque
, porque  .
. .
.
6. Mantén los ojos bien abiertos para encontrar dos soluciones para x. Si trabaja demasiado rápido, puede encontrar una respuesta al problema sin darse cuenta de que hay otra. Aquí se explica cómo encontrar los dos valores de x para líneas que se intersecan en dos puntos:
 . Si ambos factores entre paréntesis son iguales a 0, entonces la ecuación es verdadera. La única solución es
. Si ambos factores entre paréntesis son iguales a 0, entonces la ecuación es verdadera. La única solución es  →
→  . La otra solución es
. La otra solución es  →
→  .
. . Recuerda que puedes simplificar una raíz cuadrada a dos soluciones diferentes:
. Recuerda que puedes simplificar una raíz cuadrada a dos soluciones diferentes:  , y
, y . Escribe dos ecuaciones, una para cada posibilidad, y resuelve x para cada una de ellas.
. Escribe dos ecuaciones, una para cada posibilidad, y resuelve x para cada una de ellas.
7. Resolver problemas con una o cero soluciones. Dos rectas que apenas se tocan tienen una intersección y dos rectas que nunca se tocan tienen cero. Puedes reconocerlos de las siguientes maneras:
 . Solo necesitas resolver una ecuación.
. Solo necesitas resolver una ecuación. ). Escribe `sin solución` como respuesta.
). Escribe `sin solución` como respuesta.
8. Reemplaza los valores de x en la ecuación original. Una vez que tenga el valor de x de la intersección, vuelva a colocarlo en una de las ecuaciones con las que comenzó. Resolver para y para encontrar el valor de y. Si hay un segundo valor de x, repita para este valor también.
 y
y  . Una de nuestras rectas tiene la ecuación
. Una de nuestras rectas tiene la ecuación  . sustituir
. sustituir  y
y  , y resuelve cada ecuación para que obtengas
, y resuelve cada ecuación para que obtengas  y
y  si obtienes una respuesta.
si obtienes una respuesta.
9. Escribe la respuesta como coordenadas. Ahora escribes la respuesta como coordenadas, con el valor x y el valor y de la intersección. Si tiene dos respuestas, asegúrese de hacer coincidir el valor x correcto con cada valor y.
 entrada, obtenemos
entrada, obtenemos  , de modo que un punto de intersección es igual a (2, 9). Hacemos lo mismo para la segunda solución, y esto nos da el punto de intersección (-3, 4) sobre.
, de modo que un punto de intersección es igual a (2, 9). Hacemos lo mismo para la segunda solución, y esto nos da el punto de intersección (-3, 4) sobre.Consejos
- Las ecuaciones para un círculo o una elipse tienen un
término y a
término. Para encontrar la intersección de un círculo y una línea recta, resuelve x dentro de la ecuación lineal. Sustituya la solución por x en la ecuación del círculo, y la ecuación cuadrática ahora es mucho más fácil. Estos problemas pueden tener 0, 1 o 2 soluciones, como ya se indicó en los métodos anteriores.
- Un círculo y una parábola (o cualquier otra ecuación cuadrática) pueden tener 0, 1, 2, 3 o 4 soluciones. Encuentre la variable que es un cuadrado en ambas ecuaciones, digamos que es x. suelto
encendido y sustituya la respuesta por
en la otra ecuacion. Resolver y para encontrar las soluciones 0, 1 o 2. Reemplace cada solución en la ecuación cuadrática original y resuelva para x. Cada uno de estos puede tener 0, 1 o 2 soluciones.
Artículos sobre el tema. "Calcular la intersección de dos rectas"
Оцените, пожалуйста статью
Similar
Popular