Calcular el área de un cuadrado usando la diagonal: 9 pasos (con fotos)

Contenido

Pasos
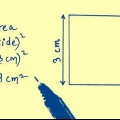
- Parte 1 de 2: Calcular el área de un cuadrado
- Parte 2 de 2: información adicional
Consejos

La fórmula más común para el área de un cuadrado es simple: es la longitud de uno de sus lados al cuadrado, o s. Pero a veces solo sabes la longitud de la diagonal de un cuadrado, la línea entre dos vértices opuestos. Si está familiarizado con los triángulos rectángulos, puede derivar una nueva fórmula con la diagonal como única variable.

Pasos

Parte 1 de 2: Calcular el área de un cuadrado

Imagen titulada Encuentra el área de un cuadrado usando la longitud de su diagonal Paso 3

1. Dibuja tu cuadrado. Un cuadrado tiene cuatro lados iguales. Digamos que cada lado tiene una longitud de `s`.

Imagen titulada Encuentra el área de un cuadrado usando la longitud de su diagonal Paso 4

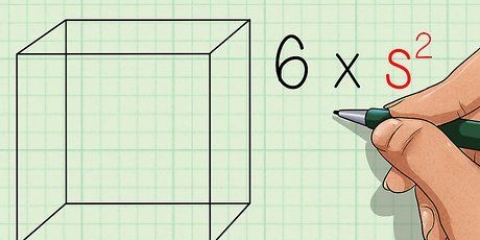
2. Usa la fórmula estándar para el área de un cuadrado. El área de un cuadrado es igual a su largo por su ancho. porque cada lado s se convierte en fórmula área = s x s = s. Esto demostrará ser útil pronto.

Imagen titulada Encuentra el área de un cuadrado usando la longitud de su diagonal Paso 5

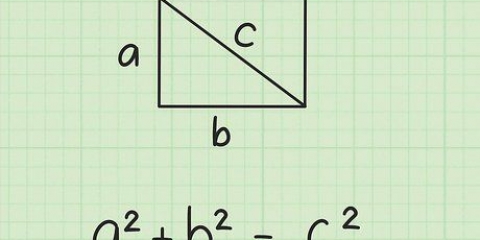
3. Conecta dos esquinas opuestas para formar una diagonal. La medida de esta diagonal se convierte en D unidades. Esta diagonal divide el cuadrado en dos triángulos rectángulos.

Imagen titulada Encuentra el área de un cuadrado usando la longitud de su diagonal Paso 6

4.Usa el teorema de Pitágoras para uno de los triángulos. El Teorema de Pitágoras es una fórmula para encontrar la hipotenusa (lado más largo) de un triángulo rectángulo: (lado A) + (lado B) = (hipotenusa) o

a 2 + B^{2} = C^{2}

$a^{2}+b^{2}=c^{2}$ . Ahora que el cuadrado se ha dividido por la mitad, puedes usar esta fórmula en uno de los triángulos rectángulos:

Los dos lados más cortos del triángulo son los lados del cuadrado: cada uno tiene una longitud s.

La hipotenusa es la diagonal del cuadrado, D.

s 2 + s^{2} = D^{2}

$s^{2}+s^{2}=d^{2}$

Imagen titulada Hallar el área de un cuadrado usando la longitud de su diagonal Paso 7

5. Ordena la ecuación para que s esté en un lado. Recuerda que sabemos que el área del cuadrado es s. Si puede aislar s en un lado, entonces tiene una nueva ecuación para el área:

s 2 + s^{2} = D^{2}

$s^{2}+s^{2}=d^{2}$

Simplificar:

2 s 2 = D^{2}

$2s^{2}=d^{2}$

Divide ambos lados por dos:

s 2 = D 22

$s^{2}={frac{d^{2}}{2}}$

Área =

s 2 = D 22

$s^{2}={frac{d^{2}}{2}}$

Área =

D 22

${frac{d^{2}}{2}}$

Imagen titulada Encuentra el área de un cuadrado usando la longitud de su diagonal Paso 9

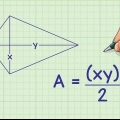
6. Usa esta fórmula con un cuadrado de ejemplo. Estos pasos han demostrado que la fórmula Área =

D 22

${frac{d^{2}}{2}}$ se aplica a todos los cuadrados. Introduzca la longitud de la diagonal para D y resolver.

Por ejemplo, supongamos que un cuadrado tiene una diagonal de 10 cm.

Área =

1022

${frac{10^{2}}{2}}$
=

\frac{100}{2}

${frac{100}{2}}$
= 50cm.

Parte 2 de 2: información adicional

1. Hallar la diagonal de la longitud de un lado. El teorema de Pitágoras para un cuadrado de lado s y diagonal D darte la formula

2 s 2 = D^{2}

$2s^{2}=d^{2}$ sobre. Resuelve para `d` si conoces las longitudes de los lados y quieres determinar la longitud de la diagonal:

$2 s 2 = D^{2}$ $2s^{2}=d^{2}$
$\sqrt{2 s} 2 = \sqrt{D} 2$ ${sqrt{2s^{2}}}={sqrt{d^{2}}}$
$s \sqrt{2} = D$ $s{raíz cuadrada{2}}=d$
Por ejemplo, si un cuadrado tiene lados de 7 cm, entonces la diagonal es d = 7√2 cm, o alrededor de 9,9 cm.
Si no tienes una calculadora, puedes usar 1.4 como una estimación de √2.

2. Determinar la longitud de un lado usando la diagonal. ¿Se da la diagonal y sabes que la diagonal de un cuadrado

s \sqrt{2}

$s{sqrt{2}}$ entonces puedes dividir ambos lados por

\sqrt{2}

${ sqrt{2}}$ a

s = \frac{D}{\sqrt{2}}

$s={frac{d}{{sqrt{2}}}}$ Llegar.

Por ejemplo, un cuadrado con una diagonal de 10 cm tiene lados de longitud

\frac{10}{\sqrt{2}} = 7, 071

${frac{10}{{sqrt{2}}}}=7,071$ cm.

Si quieres encontrar tanto la longitud de un lado como el área de la diagonal, primero puedes usar esta fórmula y luego elevar al cuadrado la respuesta del área: Área

= s 2 = 7, 071^{2} = 50

$=s^{2}=7.071^{2}=50$ cm. Esto es algo menos preciso, porque

\sqrt{2}

${ sqrt{2}}$ es un número irracional que puede tener errores de redondeo.

3. Interpretar la fórmula de la superficie. La fórmula Área =

D 22

${frac{d^{2}}{2}}$ parece ser matemáticamente correcto, pero ¿hay alguna manera de probar esto directamente?? Bien,

D 2

$d^{2}$ es el área de un segundo cuadrado con la diagonal como lado. Porque la fórmula completa

D 22

${frac{d^{2}}{2}}$ puedes razonar que este segundo cuadrado tiene exactamente el doble del área del cuadrado original. Puedes probar esto tú mismo:

Dibujar un cuadrado en papel. Asegúrate de que todos los lados sean iguales.

medir la diagonal. Dibuja un segundo cuadrado con esa longitud como los lados del cuadrado.

Traza una copia de tu primer cuadrado para que tengas dos. Recorta los tres cuadrados.

Corta los dos cuadrados más pequeños en formas que quepan dentro del cuadrado grande. Deben llenar perfectamente el espacio, para demostrar que el área del cuadrado grande es exactamente el doble del área del cuadrado más pequeño.

Consejos

Esta ecuación simple se usa en muchos campos, incluidos la cristalografía, la química y el arte. Por ejemplo, puede usarlo para calcular el área de un paisaje que ve mientras realiza una inspección o cuando usa la perspectiva en fotografía o pintura, midiendo la distancia que ha caminado e imaginando una cuadrícula de esa distancia como la diagonal.
Si desea adoptar un enfoque más visual de las matemáticas, o aprender a usar gráficos y tablas en el arte, o explorar la trayectoria en espiral de una partícula, consulte algunos artículos sobre Microsoft Excel, matemáticas, hojas de cálculo y gráficos.
Si no tiene una calculadora pero necesita una estimación más precisa de la raíz cuadrada de dos, hay maneras de hacer esto a mano. Un ejemplo de esto es el método de Newton-Raphson.