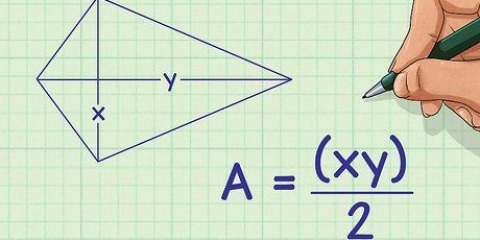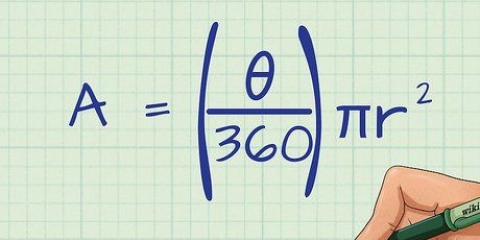En nuestro ejemplo, el área del triángulo=½ x 3 x 2=3. 
En nuestro ejemplo, A(total del pentágono)=5 x A(triángulo)=5 x 3=15. 



El base del triangulo es ½ veces el lado del pentagono. En nuestro ejemplo esto es ½ x 7=3.5 unidades. El esquina en el medio del pentágono siempre es 36º. (Suponiendo 360º para un círculo completo, puede dividirlo en 10 triángulos más pequeños. 360 ÷ 10=36, entonces el ángulo de tal triángulo es 36º). 
En un triángulo rectángulo, el es tangente de un ángulo igual a la longitud del lado opuesto, dividida por la longitud del lado adyacente. El lado opuesto al ángulo de 36º es la base del triángulo (la mitad del lado del pentágono). El lado adyacente del ángulo de 36º es la altura del triángulo. tan(36º)=opuesto / adyacente En nuestro ejemplo, tan(36º)=3.5 / altura alto x tan(36º)=3.5 altura=3.5 / bronceado(36º) altura = (aprox.) 4.8. 
En nuestro ejemplo, el área de uno de los pequeños triángulos es=½bh=½(3.5)(4.8)=8.4. 
En nuestro ejemplo, el área de todo el pentágono=8,4 x 10=84. 

Área de un pentágono regular=(5s ) / (4tan(36º)), donde s=longitud de un lado. tan(36º)=√(5-2√5). Si su calculadora no tiene una función `tan`, use la fórmula para el área: Area=(5s) / (4√(5-2√5)). 
El área de un pentágono regular=(5/2)rpecado(72º), donde r el radio es.
Calcular el área de un pentágono
Contenido
Un pentágono es un polígono de cinco lados rectos. Casi todos los problemas que encontrará en la clase de matemáticas involucrarán pentágonos regulares, con cinco lados iguales. Hay dos formas comunes de calcular el área, dependiendo de la cantidad de información que tenga.
Pasos
Método 1 de 3: Determinar el área usando los lados y la apotema

1. Comienza con la longitud del lado y la apotema. Este método funciona para pentágonos regulares, con cinco lados iguales. Además de la longitud del lado necesitas el `apotema` del pentágono. La apotema es la línea que va del centro del pentágono a un lado, que lo corta perpendicularmente (es decir, en un ángulo de 90º).
- No confundas la apotema con el radio de un polígono, porque interseca un ángulo (vértice) en lugar de un punto en el medio del lado. Si solo conoce la longitud de un lado y el radio, continúe con el siguiente método.
- Como ejemplo usamos un pentágono con lado 3 y apotema 2.

2. Divide el pentágono en cinco triángulos. Dibuja cinco líneas desde el centro del pentágono, cada una de las cuales lleva a un vértice (esquina). Ahora tienes cinco triángulos.

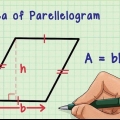
3. Calcular el area de un triangulo. Todo triángulo tiene un base igual al lado del pentágono. También tiene un altura que es igual a la apotema. (Recuerde, la altura de un triángulo es la longitud del lado que es perpendicular a su base y se extiende a un vértice). Para calcular el area de un triangulo se usa ½ x base x altura.

4. Multiplica por cinco para el área total del pentágono. Hemos dividido el pentágono en cinco triángulos iguales. Para calcular el área total, multiplica el área de un triángulo por cinco.
Método 2 de 3: determinar el área usando la longitud de un lado

1. Comience con la longitud de un lado. Este método solo funciona para pentágonos regulares, que tienen cinco lados de igual longitud.
- En este ejemplo usamos un pentágono con longitud 7 para cada lado.

2. Divide el pentágono en cinco triángulos. Dibuja una línea desde el centro del pentágono hasta un vértice. Repita para cada vértice. Ahora tienes cinco triángulos, cada uno del mismo tamaño.

3. Dividir un triangulo por la mitad. Dibuja una línea desde el centro del pentágono hasta la base de un triángulo. Esta línea debe cortar la base en un ángulo recto (90º), lo que divide el triángulo en dos triángulos iguales y más pequeños.

4. Etiqueta uno de los triángulos más pequeños. Ya podemos etiquetar un lado y un ángulo del triángulo más pequeño:

5. Calcular la altura del triangulo. El altura de este triángulo es el lado perpendicular al lado del pentágono que lleva al centro. Usamos trigonometría simple para determinar la longitud de este lado:

6.Calcular el area del triangulo. El area de un triangulo es igual a ½ base x altura. (A=½bh.) Ahora que conoce la altura, ingrese estos valores para determinar la altura de su pequeño triángulo.

7. Multiplica para hallar el área del pentágono. Uno de estos triángulos más pequeños cubre 1/10 del área del pentágono. Para el área total, multiplica el área del triángulo más pequeño por 10.
Método 3 de 3: usar una fórmula

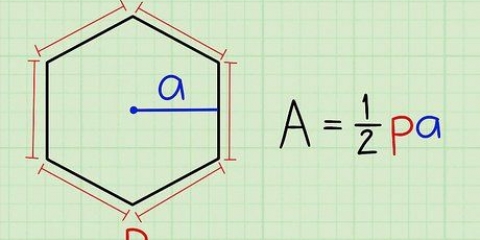
1. Usa el esquema y la apotema. La apotema es una línea desde el centro de un pentágono que corta un lado en ángulo recto. Si se da la longitud, entonces puede usar esta fórmula simple.
- Área de un pentágono regular=padre / 2, donde pags= la circunferencia y a= la apotema.
- Si no sabes la circunferencia, calcúlala usando la longitud del lado: p=5s, donde s es la longitud del lado.

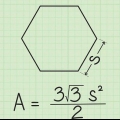
2. Usa la longitud del lado. Si solo conoce la longitud de los lados, use la siguiente fórmula:

3. Elija una fórmula que use solo el radio. Incluso puedes encontrar el área si solo conoces el radio. Utilice la siguiente fórmula:
Consejos
- Los pentágonos irregulares o los pentágonos con lados desiguales son más difíciles de estudiar. El mejor enfoque suele ser dividir el pentágono en triángulos y sumar las áreas de todos los triángulos. Es posible que también deba dibujar una forma más grande alrededor del pentágono, calcular su área y luego restar el área del espacio adicional.
- Si es posible, use un método geométrico y una fórmula, y compare los resultados para verificar su respuesta. Las respuestas pueden diferir ligeramente si completa la fórmula completamente de una sola vez (porque entonces faltan los pasos en los que completa), pero deben estar muy cerca uno del otro.
- Los ejemplos dados aquí usan valores redondeados para facilitar sus cálculos. Si tiene un polígono real con las longitudes de lado dadas, obtendrá resultados ligeramente diferentes para las otras longitudes y áreas.
- Las fórmulas se derivan de métodos geométricos, similares a los descritos aquí. Intenta descubrir cómo distraerlos tú mismo. La fórmula del radio es más difícil de derivar que las demás (pista: necesita la identidad de doble ángulo).
Artículos sobre el tema. "Calcular el área de un pentágono"
Оцените, пожалуйста статью
Popular