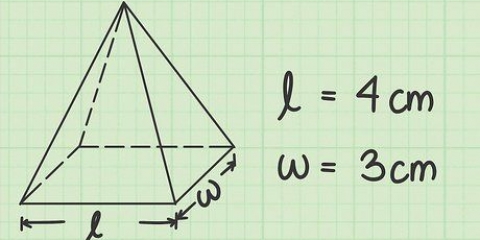Registre esta medida como a. Ejemplo: a = 2cm 
Tenga en cuenta que este paso calcula el área de una cara del cubo. Ejemplo: a = 2cm a = 2 x 2 = 4 cm 
Este paso completa el cálculo del área del cubo. Ejemplo: a = 4cm Área = 6 x a = 6 x 4 = 24 cm 

Mide la longitud de la base para determinar la longitud del prisma y asígnala a C. Ejemplo: c = 5cm Mide el ancho de la base para determinar el ancho del prisma y llámalo a. Ejemplo: a = 2cm Mide la altura del lado para determinar la altura del prisma y llámalo B. Ejemplo: b = 3cm 
Ejemplo: 2 x (a x c) = 2 x (2 x 5) = 2 x 10 = 20 cm 
Ejemplo: 2 x (a x b) = 2 x (2 x 3) = 2 x 6 = 12 cm 
Ejemplo: 2 x (b x c) = 2 x (3 x 5) = 2 x 15 = 30 cm 
Ejemplo: Área = 2ab + 2bc + 2ac = 12 + 30 + 20 = 62 cm. 

La base B, es igual a la longitud de la base del triangulo. Ejemplo: b = 4cm La altura h de la base triangular es igual a la distancia entre el borde inferior y la punta. Ejemplo: alto = 3 cm El área de un triángulo multiplicado por 2 = 2(1/2)b*h = b*h = 4*3 =12 cm 
Ejemplo: alto = 5 cm Los tres lados se refieren a los tres lados de la base triangular. Ejemplo: S1 = 2 cm, S2 = 4 cm, S3 = 6 cm 
Ejemplo: PAG = S1 + S2 + S3 = 2 + 4 + 6 = 12 cm 
Ejemplo: P x A = 12 x 5 = 60 cm 
Ejemplo: 2A + PH = 12 + 60 = 72 cm. 

Ejemplo: r = 3 cm 
Ejemplo: r = r x r = 3 x 3 = 9 cm 
Ejemplo: π*r = 3,14 x 9 = 28,26 cm 
Ejemplo: 4π*r = 4 x 28,26 = 113,04 cm 

Ejemplo: r = 3 cm Ejemplo: alto = 5 cm 
Ejemplo: Área de la base = π*r = 3,14 x 3 x 3 = 28,26 cm Ejemplo: 2π*r = 2 x 28,26 = 56,52 cm 
Ejemplo: 2π*rh = 2 x 3,14 x 3 x 5 = 94,2 cm 
Ejemplo: 2π*r + 2π*rh = 56,52 + 94,2 = 150,72 cm 

Ejemplo: largo = 3 cm Ejemplo: m = 1 cm 
Ejemplo: s = s x s = 1 x 1 = 1 cm 
Ejemplo: 2 x s x l = 2 x 1 x 3 = 6 cm 
Ejemplo: s + 2 cad = 1 + 6 = 7 cm 

Ejemplo: r = 2 cm Ejemplo: alto = 4 cm 
Ejemplo: l = √ (r + h) = √ (2 x 2 + 4 x 4) = √ (4 + 16) = √ (20) = 4,47 cm 
Ejemplo: π*r = 3,14 x 2 x 2 = 12,56 cm 
Ejemplo: π*rl = 3,14 x 2 x 4,47 = 28,07 cm 
Ejemplo: π*r + π*rl = 12,56 + 28,07 = 40,63 cm
Calcular área
Contenido
El área es el espacio total ocupado por todas las áreas de un objeto. Es la suma de todas las áreas de ese objeto. Determinar el área de una forma tridimensional es bastante fácil, siempre y cuando uses la fórmula correcta. Cada forma tiene su propia fórmula separada, por lo que primero deberá verificar qué forma es. Calcular la fórmula del área para varios objetos puede facilitar los cálculos en el futuro. Aquí discutimos algunas de las formas más comunes que puede encontrar.
Pasos
Método 1 de 7: Cubo

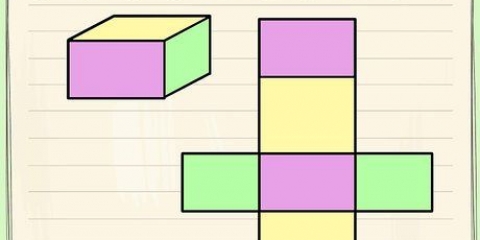
1. Definir la fórmula para el área de un cubo. Un cubo tiene seis caras idénticas. Como tanto el largo como el ancho de un cuadrado son iguales, el área de un cuadrado es a, por lo cual a la longitud es de un lado. Como un cubo tiene seis caras iguales, puedes calcular su área multiplicando el área de una de sus caras por seis. La fórmula del área de un cubo O es O = 6a, por lo cual a la longitud es de un lado.
- Las unidades de área son una determinada longitud al cuadrado: cm, dm, m, etc.

2. Mide la longitud de un lado. Por definición, cada lado o arista (arista) de un cubo debe ser igual al otro, por lo que solo necesitas medir un lado. Mide la longitud del lado con una regla. Presta atención a las unidades que usas.

3. Cuadre su medida para a. Cuadre la medida para calcular la longitud de la costilla. Elevar al cuadrado un valor significa multiplicarlo por sí mismo. Si está aprendiendo esto por primera vez, puede ser útil recordarlo como NT= 6*a*a.

4. Multiplique este producto por seis. Recuerda que un cubo tiene seis caras iguales. Ahora que conoces el área de una de las caras, multiplícala por seis (porque son las seis caras).
Método 2 de 7: Prisma rectangular

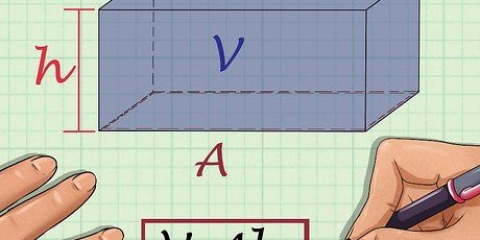
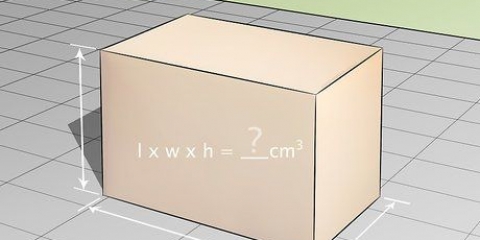
1. Definir la fórmula para el área de un prisma rectangular. Como un cubo, un prisma rectangular tiene seis caras, pero a diferencia de un cubo, esas caras no son iguales. En un prisma rectangular, solo las caras opuestas son iguales entre sí. Por lo tanto, al calcular el área de un prisma rectangular, se deben tener en cuenta las distintas longitudes de las nervaduras, como en la fórmula SA = 2ab + 2bc + 2ac.
- Para esta fórmula, a igual al ancho del prisma, B igual a la altura y C igual a la longitud.
- Si echamos un vistazo más de cerca a la fórmula, verás que simplemente sumamos todas las áreas de cada cara del objeto.
- La unidad de área será una determinada longitud al cuadrado: cm, dm, m, etc.

2. Mide el largo, alto y ancho de cada lado. Las tres lecturas pueden ser diferentes, por lo que cada una debe medirse por separado. Mide cada lado con una regla y anota el valor. Usa las mismas unidades para cada medida.

3. Calcula el área de una de las caras del prisma, y multiplícala por dos. Recuerda que hay seis caras en un prisma rectangular, y las caras opuestas son iguales entre sí. Multiplique la longitud y la altura, o C y a, encontrar el area de un plano. Tome esta medida y multiplíquela por dos para tener en cuenta el plano idéntico opuesto.

4. Encuentra el área de la otra cara del prisma y multiplícala por dos. Al igual que con el primer conjunto de caras, multiplique el ancho y la altura, o a y B para determinar el área de otra cara del prisma. Multiplique esta medida por dos para tener en cuenta los lados idénticos opuestos.

5. Calcula el área de los extremos del prisma y multiplícalo por dos. Las otras dos caras del prisma son los extremos. Multiplique el largo y el ancho (C y B) para encontrar su superficie. Multiplique esta área por dos para tener en cuenta ambos lados.

6. Agregue las tres áreas separadas juntas. Dado que el área del prisma es el área total de todas las caras de un objeto, el último paso es sumar todas las áreas calculadas individualmente. Sume las áreas de todos los lados para obtener el área total.
Método 3 de 7: Prisma triangular

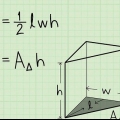
1. Definir la fórmula del área de un prisma triangular. Un prisma triangular tiene dos caras triangulares idénticas y tres caras rectangulares. Para encontrar el área, hay que calcular el área de todas las caras y sumarlas. El área de un prisma triangular es SA = 2A + PH, donde A es el área de la base triangular, P es el perímetro de la base triangular y h es la altura del prisma.
- Para esta fórmula se cumple que a el area de un triangulo y por lo tanto A = 1/2bh, por lo cual B es la base del triangulo y h la altura.
- pags es el perímetro del triángulo calculado sumando las tres aristas del triángulo.
- Las unidades de área es una unidad de longitud al cuadrado: cm, dm, m, etc.

2. Calcula el área del plano triangular y multiplícalo por dos. El área de un triángulo es /2b*h donde b es la base del triángulo y h es la altura. Entonces, como hay dos triángulos idénticos como caras, multiplicamos la fórmula por dos. Esto facilita el cálculo para ambos planos (b*h).

3. Mide cada lado del triángulo y la altura del prisma. Para completar el cálculo del área, necesitas saber la longitud de cada lado del triángulo y la altura del prisma. La altura es la distancia entre las dos caras triangulares.

4. Encuentra el perímetro del triángulo. El perímetro del triángulo se puede calcular sumando todos los lados medidos: S1 + S2 + S3.

5. Multiplica la circunferencia de la base por la altura del prisma. Recuerda que la altura del prisma es la distancia entre las dos caras triangulares. En otras palabras, multiplica pags de eh.

6. Sume las dos lecturas separadas. Debes sumar las dos medidas de los dos pasos anteriores para obtener el área del prisma triangular.
Método 4 de 7: Bol

1. Definir la fórmula del área de una esfera. Una esfera tiene una superficie curva, por lo que el área de la superficie es un valor multiplicado por la constante, pi. El área de una esfera se calcula mediante la ecuación NT = 4π*r.
- Para esta fórmula, r igual al radio de la esfera. Pi (o π) se puede redondear a 3,14.
- Las unidades del área serán una unidad de longitud, al cuadrado: cm, dm, m, etc.

2.medir el radio de la bombilla. El radio de la esfera es la mitad del diámetro, o la distancia desde el centro de la esfera hasta el borde.

3. Cuadrar el radio. Para elevar al cuadrado un número, multiplícalo por sí mismo. Multiplica la medida por r con el mismo. Recuerda que esta fórmula se puede reescribir como SA = 4π*r*r.

4. Multiplique el radio al cuadrado por un redondeo de Pi. Pi es una constante que representa la relación entre la circunferencia de un círculo y su diámetro. Es un número irracional con muchos dígitos después del punto decimal. A menudo se redondea a 3,14. Multiplica el radio al cuadrado por π, o 3,14, por el área de una sección transversal circular de la esfera.

5. Multiplique este producto por cuatro. Para completar el cálculo, multiplícalo por cuatro. Encuentra el área de la esfera multiplicando el área circular plana por cuatro.
Método 5 de 7: Cilindro

1. Definir la fórmula del área de un cilindro. Un cilindro tiene dos extremos circulares que cierran una superficie tubular. La fórmula del área de un cilindro es NT = 2π*r + 2π*rh, por lo cual r es igual al radio de la base circular y h es igual a la altura del cilindro. ronda Pi (o π) disminuye a 3.14.
- La fórmula 2π*r calcula el área de los dos extremos circulares, mientras que 2πrh es el área de la columna entre los dos extremos.
- Las unidades de área son una unidad de longitud al cuadrado: cm, dm, m, etc.

2. Medir el radio y la altura del cilindro. El radio de un círculo es la mitad de su diámetro, o la distancia desde el centro del círculo hasta el borde. La altura es la distancia total del cilindro de un extremo al otro. Dibuja estas medidas con una regla y anótalas.

3. Encuentra el área de la base y multiplícala por dos. Para encontrar el área de la base, usa la fórmula del área o un círculo (π*r). Para completar el cálculo, eleve el radio al cuadrado y multiplíquelo por Pi. Luego multiplique por dos debido al segundo círculo idéntico en el otro extremo del cilindro.

4. Calcula la superficie del propio cilindro con 2π*rh. Esta es la fórmula para calcular el área de un tubo. El tubo es el espacio entre los dos extremos circulares del cilindro. Multiplica el radio por dos, Pi y la altura.

5. Sume las dos lecturas separadas. Suma el área de los dos círculos al área del espacio entre los dos círculos para calcular el área total del cilindro. Nota: Al sumar estas dos piezas reconoces la fórmula original: NT =2π*r + 2π*rh.
Método 6 de 7: pirámide cuadrada

1. Definir la fórmula del área para una pirámide cuadrada. Una pirámide cuadrada tiene una base cuadrada y cuatro lados triangulares. Como se mencionó, el área de un cuadrado es la longitud de un lado al cuadrado. El área de un triángulo es 1/2sl (el lado del triángulo por la longitud o la altura del triángulo). Como hay cuatro triángulos, calculas el área total multiplicando eso por cuatro. Al sumar todas estas caras, se obtiene la ecuación del área de una pirámide cuadrada: NT = s + 2 canales.
- En esta ecuación, s la longitud de cada lado de la base cuadrada y yo la altura inclinada de cada lado triangular.
- La unidad de área es una determinada unidad de longitud al cuadrado: cm, dm, m, etc.

2. Mida la altura inclinada y el lado de la base. La altura oblicua yo, es la altura de uno de los lados triangulares. Es la distancia desde la base hasta la punta de la pirámide, medida a lo largo de un lado plano. El lado básico s, es la longitud de un lado de la base cuadrada. Como la base es cuadrada, esta medida es la misma para todos los lados. Usa una regla para cada medida.

3. Halla el área de la base cuadrada. El área de una base cuadrada se puede calcular elevando al cuadrado la longitud de un lado (s multiplicar por sí mismo).

4. Calcula el área total de las cuatro caras triangulares. La segunda parte de la ecuación es el área de las cuatro caras triangulares restantes. Usando la fórmula 2ls, multiplicamos s de yo y dos. Halla el área de cada cara.

5. Añadir las dos áreas separadas juntas. Suma el área total de las caras al área de la base para calcular el área total.
Método 7 de 7: Cono

1. Definir la fórmula del área de un cono. Un cono tiene una base circular y una superficie redonda que se estrecha en un punto. Para encontrar el área, toma el área de la base circular y el área del cono, y suma los dos. La fórmula del área de un cono es: SA = π*r + π*rl, por lo cual r el radio es desde la base circular, yo la altura oblicua del cono, y π es la constante pi (3.14).
- La unidad de área es una determinada unidad de longitud al cuadrado: cm, dm, m, etc.

2. Mide el radio y la altura del cono. El radio es la distancia desde el centro de la base circular hasta el borde de la base. La altura es la distancia desde el centro de la base hasta la punta del cono, medida a través del centro del cono.

3. Calcular la altura de la pendiente (yo) del cono. Dado que la altura oblicua es la hipotenusa real de un triángulo, necesitas encontrar la usando el teorema de Pitágoras para calcularlo. Usar la forma reorganizada, l = √ (r + h), por lo cual r el radio es y h la altura del cono.

4. Encuentra el área de la base circular. El área de la base se calcula con la fórmula π*r. Después de medir el radio, lo elevas al cuadrado (así lo multiplicas por sí mismo) y luego multiplicas ese producto por pi.

5. Calcular el área de la parte superior del cono. Utilice la fórmula π*rl, donde r el radio es del circulo y yo la pendiente como se calculó anteriormente, para determinar el área de la parte superior del cono.

6. Sume las dos áreas para obtener el área total del cono. Calcula el área final del cono sumando el área de la base circular al calcular el paso anterior.
Artículos de primera necesidad
- Gobernante
- bolígrafo o lápiz
- Papel
Artículos sobre el tema. "Calcular área"
Оцените, пожалуйста статью
Popular