Cómo calcular el área de un triángulo isósceles (con imágenes)

Contenido

Pasos
- Método 1 de 2: determinar el área usando las longitudes de cada lado
- Método 2 de 2: usar trigonometría
Consejos

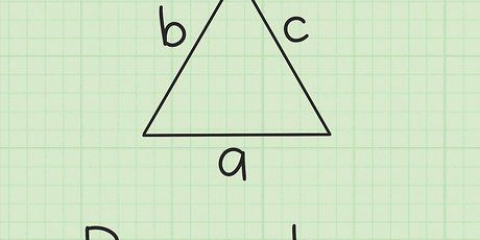
Un triangulo isosceles es un triangulo con dos lados de la misma longitud. Estos dos lados iguales siempre tienen el mismo ángulo con la base (el tercer lado) y se encuentran directamente sobre el centro de la base. Puedes probar esto por ti mismo con una regla y dos lápices de la misma longitud: si intentas inclinar el triángulo en una dirección, los extremos de los lápices no se juntarán. Con estas propiedades especiales del triángulo isósceles, el área se puede calcular con solo unos pocos datos.

Pasos

Método 1 de 2: determinar el área usando las longitudes de cada lado

Imagen titulada Hallar el área de un triángulo isósceles Paso 1

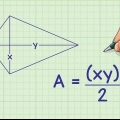
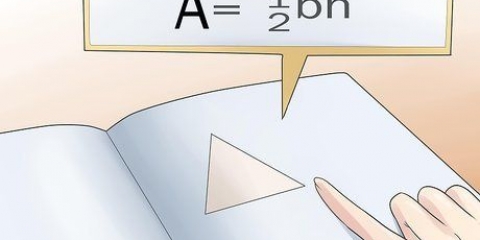
1. Tomar el área de un paralelogramo. Los cuadrados y los rectángulos son paralelogramos, como cualquier forma de cuatro lados donde dos pares de lados son paralelos entre sí. Todos los paralelogramos tienen una fórmula de área simple: el área es igual a la base multiplicada por la altura, o A = bh. Si colocas un paralelogramo imaginario en posición vertical sobre una superficie horizontal, la base es la longitud del lado en el que está la figura. La altura es la distancia desde la base hasta el punto más alto (como era de esperar); es decir, la distancia desde la base hasta el lado opuesto. Mida siempre la altura en ángulo recto (90 grados) con respecto a la base.

Para cuadrados y rectángulos, la altura es igual a la longitud de un lado vertical, ya que estos lados están en ángulo recto con el suelo.

Imagen titulada Encuentra el área de un triángulo isósceles Paso 2

2. Compara triángulos y paralelogramos. Hay una relación simple entre estas dos formas. Cortar un paralelogramo por la mitad a lo largo de la diagonal lo divide en dos triángulos iguales. Del mismo modo, puedes unir dos triángulos idénticos para formar un paralelogramo. Esto significa que el área de un triángulo se puede escribir como A = bh, exactamente la mitad del tamaño de un paralelogramo correspondiente.

Imagen titulada Hallar el área de un triángulo isósceles Paso 3

3. Encuentra la base del triangulo isosceles. Ahora tienes la fórmula, pero ¿qué son exactamente la `base` y la `altura` de un triángulo isósceles?? La base es la parte fácil: solo toma el tercer lado desigual del triángulo isósceles.

Por ejemplo, si un triángulo isósceles tiene lados de 5 cm, 5 cm y 6 cm, entonces el lado de 6 cm es la base.

Si un triángulo tiene tres lados iguales (y por lo tanto es equilátero), entonces puedes elegir cualquier lado como base. Un triángulo equilátero es un tipo especial de triángulo isósceles, pero puedes encontrar su área de la misma manera.

Imagen titulada Hallar el área de un triángulo isósceles Paso 4

4. Dibuja una línea entre la base y el vértice opuesto. Asegúrese de que la línea toque la base en ángulo recto. La longitud de esta línea es la altura del triángulo y, por lo tanto, está etiquetada h. Una vez que obtenga el valor de h calculado, puede determinar el área.

En un triángulo isósceles, esta línea siempre toca la base en su centro exacto.

Imagen titulada Encuentra el área de un triángulo isósceles Paso 5

5. Ver la mitad del triángulo isósceles. Tenga en cuenta que la altura divide el triángulo isósceles en dos triángulos rectángulos idénticos. Mira uno de ellos y señala los tres lados:

Uno de los lados cortos es igual a la mitad de la base:

\frac{B}{2}

${frac{b}{2}}$ .

El otro lado corto es la altura h.

La hipotenusa (hipotenusa) del triángulo rectángulo es uno de los dos lados iguales del triángulo isósceles. consigamos esto s mencionar.

Imagen titulada Hallar el área de un triángulo isósceles Paso 6

6.Usa el teorema de Pitágoras. Si conoces dos lados de un triángulo rectángulo y quieres encontrar el tercero, puedes usar el Teorema de Pitágoras: (lado 1) + (lado 2) = (hipotenusa) Sustituye las variables que usamos en este problema y obtienes

(\frac{B}{2})^{2} + h^{2} = s^{2}

$({frac{b}{2}})^{2}+h^{2}=s^{2}$ .

Probablemente aprendiste el teorema de Pitágoras si

a 2 + B^{2} = C^{2}

$a^{2}+b^{2}=c^{2}$ . Escribir esto como `lados` e `hipotenusa` evita que los confundas con las variables del triángulo.

Imagen titulada Hallar el área de un triángulo isósceles Paso 7

7. Resolver h. Recuerda que tienes la fórmula del área B y h usado, pero que no sabes el valor de h aún no lo sé. Reescribe la fórmula h resolver:

(\frac{B}{2})^{2} + h^{2} = s^{2}

$({frac{b}{2}})^{2}+h^{2}=s^{2}$

h 2 = s^{2} - (\frac{B}{2})^{2}

$h^{2}=s^{2}-({frac{b}{2}})^{2}$

h = \sqrt{(} s^{2} - (\frac{B}{2})^{2})

$h={raíz cuadrada(}s^{2}-({frac{b}{2}})^{2})$ .

Imagen titulada Hallar el área de un triángulo isósceles Paso 8

8. Sustituye los valores de tu triángulo por h Ahora que conoces esta fórmula, puedes usarla para un triángulo isósceles cuyos lados conoces. Sólo tienes que introducir la longitud de la base para B y la longitud de uno de los lados iguales para s, y calcula despues h.

Por ejemplo, tienes un triángulo isósceles con lados de 5 cm, 5 cm y 6 cm. B = 6 y s = 5.

Usa estos valores en tu fórmula:

h = \sqrt{(} s^{2} - (\frac{B}{2})^{2})

$h={raíz cuadrada(}s^{2}-({frac{b}{2}})^{2})$

h = \sqrt{(} 5^{2} - (\frac{6}{2})^{2})

$h={raíz cuadrada(}5^{2}-({frac{6}{2}})^{2})$

h = \sqrt{(} 25 - 3^{2})

$h={raíz cuadrada(}25-3^{2})$

h = \sqrt{(} 25 - 9)

$h={raíz cuadrada(}25-9)$

h = \sqrt{(} dieciséis)

$h={raíz cuadrada(}16)$

h = 4

$h=4$ cm.

Imagen titulada Encuentra el área de un triángulo isósceles Paso 9

9. Use los valores de base y altura en la fórmula del área. Ahora tienes lo que necesitas para usar la fórmula del principio de esta sección: Área = ½bh. Sustituye los valores de b y h en esta fórmula y calcula la respuesta. No olvides escribir tu respuesta en unidades cuadradas.

Para continuar con el ejemplo: el triángulo 5-5-6 tiene una base de 6 cm y una altura de 4 cm.

A = bh
A = ½(6cm)(4cm)
A = 12 cm.

Imagen titulada Encuentra el área de un triángulo isósceles Paso 10

10. Prueba un ejemplo más difícil. La mayoría de los triángulos isósceles son más difíciles de trabajar que en el ejemplo anterior. La altura a menudo contiene una raíz cuadrada que no se puede simplificar a un número entero. Si este es el caso, deje la altura como la raíz cuadrada en el la forma mas simple estar de pie. Aquí hay un ejemplo:

Cual es el area de un triangulo de lados 8 cm, 8 cm y 4 cm?

El lado impar mide 4 cm y la base B.

La altura

h = \sqrt{8} 2 - (\frac{4}{2})^{2}

$h={raíz cuadrada{8^{2}-({frac{4}{2}})^{2}}}$

= \sqrt{64 - 4}

$={raíz cuadrada{64-4}}$

= \sqrt{60}

$={raíz cuadrada{60}}$

Simplifica la raíz cuadrada factorizando:

h = \sqrt{60} = \sqrt{4 * 15} = \sqrt{4} \sqrt{15} = 2 \sqrt{15} .

$h={sqrt{60}}={sqrt{4*15}}={sqrt{4}}{sqrt{15}}=2{sqrt{15}}$

Superficie

= \frac{1}{2} B h

$={frac{1}{2}}bh$

= \frac{1}{2} (4) (2 \sqrt{15})

$={frac{1}{2}}(4)(2{sqrt{15}})$

= 4 \sqrt{15}

$=4{raíz cuadrada{15}}$

Deje esta respuesta como se indica, o use una calculadora para una estimación decimal (alrededor de 15,49 cm2).

Método 2 de 2: usar trigonometría

Imagen titulada Hallar el área de un triángulo isósceles Paso 11

1. Empezar con un lado y una esquina. Si está familiarizado con la trigonometría, entonces puede encontrar el área de un triángulo isósceles incluso si no conoce ninguna de las longitudes de sus lados. Aquí hay un problema de ejemplo donde solo se conoce lo siguiente:

La longitud s de los dos lados iguales mide 10 cm.
El ángulo θ entre los dos lados iguales es de 120 grados.

Imagen titulada Encuentra el área de un triángulo isósceles Paso 12

2. Divide el triángulo isósceles en dos triángulos rectángulos. Dibuja una línea hacia abajo desde el vértice entre los dos lados iguales, cortando la base en un ángulo recto. Ahora tienes dos triángulos rectángulos iguales.

Esta recta divide a θ perfectamente por la mitad. Todo triángulo rectángulo tiene un ángulo de ½θ, o en este caso (½)(120) = 60 grados.

Imagen titulada Hallar el área de un triángulo isósceles Paso 13

3. Usa la trigonometría para determinar el valor de h. Ahora que tienes un triángulo rectángulo, puedes aplicar las funciones trigonométricas (seno, coseno y tangente). En el problema de ejemplo, sabes cuál es la hipotenusa y quieres el valor de h saber, el lado al lado del ángulo conocido. Usa el hecho de que coseno = adyacente / hipotenusa para h resolver:

cos(θ/2) = h / s

cos(60º) = h / 10

h = 10cos(60º)

Imagen titulada Hallar el área de un triángulo isósceles Paso 14

4. Determinar el valor del lado restante. Hay un lado aún desconocido del triángulo rectángulo, que usted X puede nombrar. Resuelve esto con la definición seno = opuesto / hipotenusa:

sen(θ/2) = x / s

sen(60º) = x / 10

x = 10sen(60º)

Imagen titulada Hallar el área de un triángulo isósceles Paso 15

5. Usa la relación de x con la base del triángulo isósceles. Ahora puede `alejarse` al triángulo isósceles en cuestión. La base B de ese ángulo es igual a 2X, ya que estaba dividido en dos segmentos, cada uno con una longitud X.

Imagen titulada Hallar el área de un triángulo isósceles Paso 16

6. Usa los valores h y B en la formula del area del triangulo. Ahora que conoce la base y la altura, puede aplicar la fórmula estándar A = ½bh:

a = \frac{1}{2} B h

$A={frac{1}{2}}bh$

= \frac{1}{2} (2 X) (10 C O s 60)

$={frac{1}{2}}(2x)(10cos60)$

= (10 s I norte 60) (10 C O s 60)

$=(10sen60)(10cos60)$

= 100 s I norte (60) C O s (60)

$=100sen(60)cos(60)$

Usando una calculadora (ajustada a grados), obtienes aproximadamente 43,3 cm2 como respuesta. Alternativamente, use las propiedades de la trigonometría para simplificarlas a A = 50sin(1200).

Imagen titulada Hallar el área de un triángulo isósceles Paso 17

7. Reescribe esto como una fórmula universal. Ahora que sabe cómo solucionar esto, puede aplicar la fórmula general sin pasar por todo el proceso cada vez. Esto es lo que obtienes si repites este proceso, sin usar valores específicos (y simplificando usando las propiedades trigonométricas):

a = \frac{1}{2} s^{2} s I norte θ

$A={frac{1}{2}}s^{2}sentheta$

s es la longitud de uno de los dos lados iguales.

Θ es el ángulo entre los dos lados iguales.

Consejos

Si se trata de un triángulo rectángulo isósceles (dos lados iguales y un ángulo de 90 grados), es mucho más fácil encontrar el área. Si usa uno de los lados cortos como base, el otro lado corto es la altura. Ahora la fórmula A = ½ b * h se puede simplificar a ½s, donde s es la longitud de un lado corto.
Las raíces cuadradas tienen dos soluciones, una positiva y otra negativa, pero puedes ignorar el negativo en geometría. Por ejemplo, no puede tener un triángulo con una `altura negativa`.
Algunos problemas trigonométricos te dan otra información para empezar, como la longitud de la base y un ángulo (y el hecho de que el triángulo es isósceles). La estrategia básica sigue siendo la misma: dividir el triángulo isósceles en triángulos rectángulos y calcular la altura usando funciones trigonométricas.