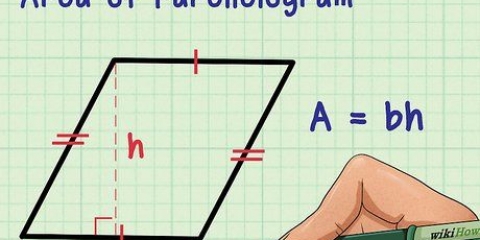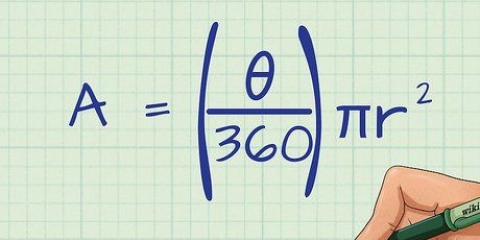Cómo calcular el área de un cuadrilátero

Contenido

Pasos

Así que para tu tarea tienes que calcular el área de un cuadrilátero...pero no tienes ni idea de lo que es un cuadrilátero. No se asuste, el rescate está cerca! Un cuadrilátero es cualquier figura que consta de 4 lados/ángulos. Todo lo que tienes que hacer es determinar el tipo de cuadrilátero del problema y usar la fórmula correspondiente para calcular el área.

Pasos

Método 1 de 4: cuadrados, rectángulos y otros paralelogramos

1. Aprende a determinar qué es un paralelogramo. Un paralelogramo es cualquier cuadrilátero con 2 pares de lados paralelos, donde los lados paralelos tienen la misma longitud. Los cuadrados, rectángulos y rombos son todos paralelogramos.

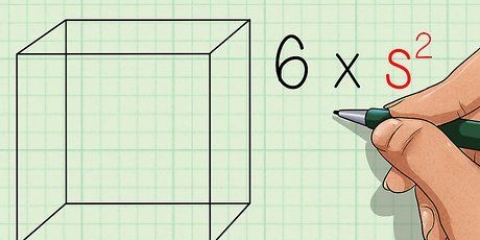
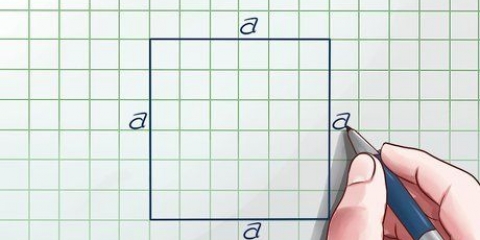
2. Hallar el area de un cuadrado. Dado que cada lado de un cuadrado tiene la misma longitud, todo lo que necesitas hacer es medir la longitud de 1 lado (llámalo "t"), para hallar el área de un cuadrado. Esto es lo mismo que multiplicar la base del cuadrado por su altura; la base y la altura son siempre las mismas. Utilice la siguiente fórmula:

k = t

Esto es lo mismo que K = t * t

Si un lado de un cuadrado tiene una longitud de 4, (t = 4), entonces el área es t, o 4 x 4 = 16.

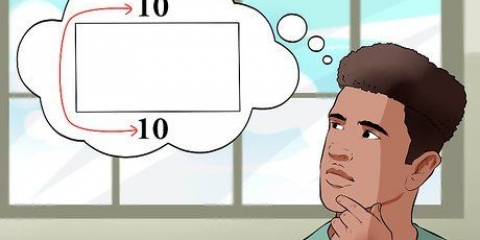
3. encontrar el area de un rectangulo. Para encontrar el área de un rectángulo es necesario saber el largo y el ancho del rectángulo. La fórmula es la siguiente:

K = fondo*h

Si el largo es largo 10 y el ancho es 5, entonces el área del rectángulo es 10 x 5 (largo x ancho) = 50.

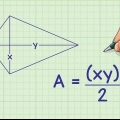
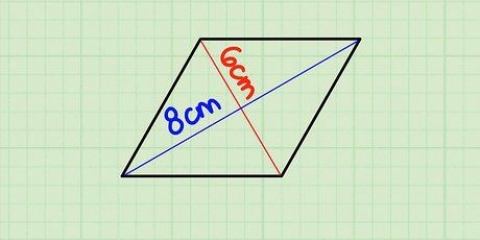
4. Hallar el area de un cuadrado. Esto puede ser complicado: no puedes simplemente multiplicar un lado por el otro aquí. Ahora tendrá que dibujar líneas desde cada punto y medir las diagonales de la forma, si no se proporciona. Luego multiplica las diagonales así:

K = (b*h)/2, para lo cual b = diagonal 1 y h = diagonal 2

Si un cuadrado tiene diagonales de longitud 6 y luego 8, entonces el área es (6 x 8)/2 = 48/2 = 24

Método 2 de 4: El área de un trapecio

1. Determinar si es un trapezoide. Un trapezoide es un cuadrilátero con al menos 2 lados paralelos. Cada uno de los cuatro lados de un trapezoide puede tener una longitud diferente. Hay dos formas diferentes de encontrar el área de un trapezoide, dependiendo de la información dada.

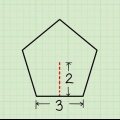
2. Determinar la altura del trapezoide. La altura de un trapezoide es la línea perpendicular que conecta la línea de base superior y la línea de base inferior, y las necesita a ambas para calcular el área. Esto es no de la misma longitud que uno de los lados, porque cada lado es diagonal. Así es como se encuentra la altura:

Determinar cuál es la base más corta. Coloque su lápiz en la esquina entre la línea de base y dibuje una línea recta hacia arriba o hacia abajo hasta la otra línea de base. Ahora deberías haber dibujado un triángulo con un ángulo de 90 grados.

Usa la trigonometría para determinar la altura. Por ejemplo, si conoce la longitud de un lado y se conoce el ángulo adyacente, y hay un ángulo de 90 grados en el triángulo, entonces la altura es la longitud del lado por el seno del ángulo.

Supongamos que la altura del trapezoide es 10.

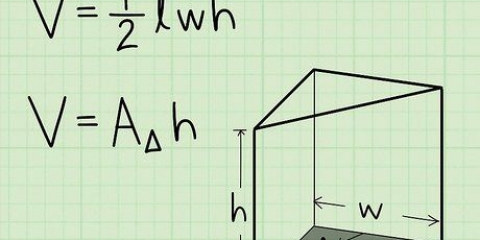
3. Determine el área del trapezoide usando la altura y la longitud de la base. Si conoce la altura del trapezoide y la longitud de ambos lados de la base, use la siguiente fórmula:

K = (a+b)/2 * h

Si la altura es 10 y la base tiene una longitud de 7 y 9, entonces puedes encontrar el área calculando: (7 + 9)/2 * 10 = (16/2) * 10 = 8 * 10 = 80

4. Encuentra el área de un trapezoide usando el segmento medio. Este segmento medio es una línea que corre paralela a las líneas inferior y superior del trapezoide y tiene una longitud exactamente en el medio. Así es como trabajas:

Determinar el segmento medio. Para determinar la longitud del segmento medio metro, sacamos el promedio de las longitudes de los lados a y B (o la línea inferior y superior del trapezoide).Usa la fórmula: m = (a+b)/2.Ahora que conoce la longitud del segmento medio, puede multiplicarlo por la altura para encontrar el área. Utilice la siguiente fórmula:

K = m*h

Esta es esencialmente la misma fórmula que la original, pero ahora reemplaza "metro" el término (a + b)/2.

Suponga que conoce el segmento medio de este trapecio. Supongamos que esto es 8, entonces el área del trapezoide es 8 x 10 = 80, al igual que con el método anterior.

Método 3 de 4: determinar la superficie de una cometa

1. que es una cometa. Una cometa se define como una forma geométrica donde 2 pares de lados de igual longitud están conectados entre sí, lo que se asemeja a una cometa normal. Hay dos formas diferentes de encontrar el área de esta figura, dependiendo de la información dada.

2. Encuentra el área de una cometa usando la longitud de sus lados. Si conoce la longitud de dos lados diferentes de una cometa y conoce el ángulo entre esos lados, use la siguiente fórmula donde el ángulo es igual a theta (θ):

K =(a*b) * sen θ

3. Encuentra el área de una cometa usando las diagonales. Una diagonal es la línea recta entre dos esquinas opuestas de la cometa. Cada cometa tiene 2 diagonales.

Determinar la longitud de cada diagonal. Dibuja una línea desde una esquina de una cometa hasta la opuesta. Ahora deberías tener 2 triángulos. Determinar usando Este artículo, cual es la longitud de la diagonal (los 3 angulos de un triangulo suman 180 grados).

Una vez que haya determinado la primera diagonal, use los mismos principios para determinar la longitud de la otra. Luego usa esta fórmula para determinar el área, donde pags y q representan la longitud de las diagonales:

K = (p*q)/2

Si las diagonales tienen longitudes de 4 y 6, entonces puedes encontrar el área de la cometa de la siguiente manera: (4 x 6)/2 = 24/2 = 12

Tenga en cuenta que esta fórmula también funciona para el área de un rombo, ya que este es un tipo especial de cometa, donde todos los lados tienen la misma longitud.

Método 4 de 4: una fórmula general

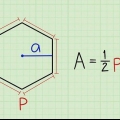
1. La fórmula general para determinar el área de un cuadrilátero. Existen fórmulas para determinar el área de cualquier cuadrilátero, independientemente de su forma. Aquí está la forma más general, usando principios trigonométricos:

Si k es el área total del cuadrilátero, a, B, C y D representan las longitudes de los 4 lados, a es el ángulo (en grados) entre los lados a y D y C es el ángulo (en grados) entre los lados B y C, entonces:
k = 0.5*a*d * sin A + 0.5*b*c * pecado C
Si estás tratando de encontrar el área de un paralelogramo donde los ángulos opuestos son iguales, la fórmula se vuelve más simple: k = 0.5*(ad + bc) * sin A.