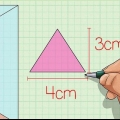
Ej: si la altura de la base triangular es 5 cm y la base del prisma triangular es 4 cm, entonces el área de la base es 1/2 x 5 cm x 4 cm, igual a 10 cm. 

Ej: 10 cm x 7 cm = 70 cm 


Ej: Longitud = 3 cm. 
Ej: 3 cm = 3 cm. * 3cm. * 3cm. = 27 centímetros. 


Ej: Longitud = 10 cm. 
Ej: Ancho = 8 cm. 
Ej: Altura = 5 cm. 
Ej: 10 cm. * 8cm. * 5 cm = 400 cm. 


Supongamos que la base 1 = 8 cm, la base 2 = 6 cm y la altura = 10 cm. Ej: 1/2 x (6 + 8) x 10 = 1/2 x 14 cm x 10 cm = 80 cm. 

80cm x 12cm = 960cm. 


A = 1/2 x 5 x lado x apotema A = 1/2 x 5 x 6 cm x 7 cm = 105 cm 

105 cm x 10 cm = 1050 cm 
Calcular el volumen de un prisma
Un prisma es una figura geométrica con dos extremos idénticos y lados planos. El prisma lleva el nombre de la forma de su base, así que un prisma con una base triangular se llama "prisma triangular." Para calcular el volumen de un prisma, todo lo que necesitas hacer es calcular el área de la base y multiplicarla por la altura; calcular el área de la base puede ser la parte complicada. He aquí cómo calcular el volumen de varios prismas.
Pasos
Método 1 de 5: calcular el volumen de un prisma triangular

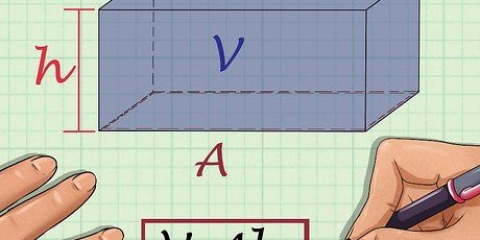
1. Escribe la fórmula para hallar el volumen de un prisma triangular. la fórmula es V = 1/2 x largo x ancho x alto. Pero, desglosamos esta fórmula aún más, para obtener la fórmula V = área o base x altura usar. Puede calcular el área de la base usando la fórmula para encontrar el área de un triángulo: multiplique 1/2 por la longitud y el ancho de la base.

2. Determinar el área del plano base. Para encontrar el volumen de un prisma triangular, primero debes determinar el área de la base triangular. Encuentra el área de la base del prisma multiplicando 1/2 por la base del triángulo por la altura.

3. determinar la altura. Supongamos que la altura de este prisma triangular es de 7 cm.

4. Multiplica el área de la base triangular por la altura. Multiplica el área de la base por la altura. Multiplica la base por la altura y obtendrás el volumen del prisma triangular.

5. Da tu respuesta en unidades cúbicas. Siempre debe usar unidades cúbicas al calcular un volumen porque está trabajando con objetos tridimensionales. La respuesta final es 70 cm.
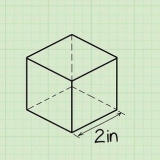
Método 2 de 5: calcular el volumen de un cubo

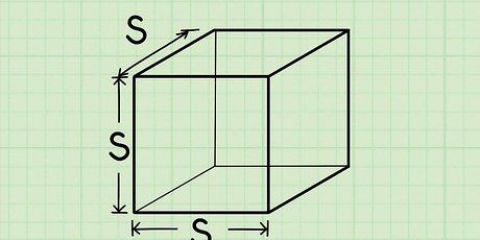
1. Escribe la fórmula para hallar el volumen de un cubo. la fórmula es V = lado. Un cubo es un prisma con 3 lados iguales.

2. Determinar la longitud de 1 lado del cubo. Todos los lados son iguales, así que no importa cuál elijas.

3. El poder de tres. Multiplica el número por sí mismo dos veces para obtener el número cúbico. un ejemplo es "un x un x un". Como todas las longitudes de los lados son iguales, multiplica dos lados por el área de la base y un tercer lado por la altura. Puedes pensar en esto como una multiplicación de la longitud, la anchura y la altura, que son todas iguales.

4. Da tu respuesta en unidades cúbicas.. La respuesta final es 27 cm.
Método 3 de 5: calcular el volumen de un prisma rectangular

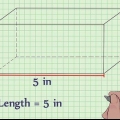
1. Escribe la fórmula para hallar el volumen de un prisma rectangular. la fórmula es V = largo * ancho * alto. Un prisma rectangular es un prisma de base rectangular.

2. determinar la longitud. La longitud es el lado más largo de la superficie plana del rectángulo, por encima o por debajo del prisma rectangular.

3. determinar el ancho. El ancho del prisma rectangular es el lado más corto de la superficie plana de un rectángulo, en la parte superior o inferior de la forma.

4. determinar la altura. La altura es la parte del prisma rectangular que está en posición vertical. Puedes imaginar la altura del prisma rectangular como esa parte que se extiende desde un rectángulo y forma una figura tridimensional.

5. Multiplica el largo, el ancho y el alto. Multiplique estos en cualquier orden para el producto. Usa este método para encontrar el área de la base rectangular (10 x 8) y luego el volumen multiplicándolo por la altura, 5. Sin embargo, para encontrar el volumen de este prisma, puedes multiplicar las longitudes del are en cualquier orden.

6. Da tu respuesta en unidades cúbicas. La respuesta final es 400 cm.
Método 4 de 5: calcular el volumen de un prisma trapezoidal

1. Escribe la fórmula para calcular el volumen de un trapezoide. La fórmula es: V = [1/2 x (base1 + base2) x altura] x altura del prisma. Usa la primera parte para el área de la base del prisma antes de continuar.

2. Halla el área de la base. Para hacer esto, ingrese el área de la parte superior e inferior en la fórmula, junto con la altura.

3. Determinar la altura del prisma. Supongamos que la altura del prisma es de 12 cm.

4. Multiplica el área de la base por la altura. Para calcular el volumen del trapecio, multiplica el área de la base por la altura.

5. Da tu respuesta en unidades cúbicas. La respuesta final es 960 cm
Método 5 de 5: Calcula el volumen de un prisma pentagonal regular

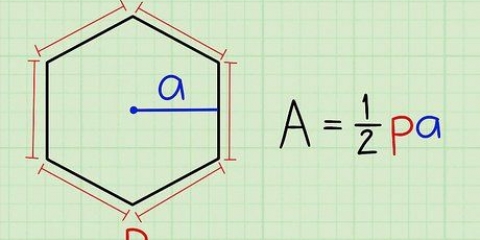
1. Escriba la fórmula para encontrar el volumen de un prisma pentagonal regular. la fórmula es V = [1/2 x 5 x lado x apotema] x altura del prisma. Puedes usar la primera parte de la fórmula para encontrar el área de la base pentagonal. Piensa en esto como determinar el área de los 5 triángulos que juntos forman un polígono regular. El lado es el ancho de 1 triángulo, y la apotema es la altura de uno de los triángulos.Ahora multiplicas por 1/2 porque eso es parte de encontrar el área de un triángulo y luego lo multiplicas por 5 porque hay 5 triángulos en un pentágono.
- Para obtener más información sobre cómo determinar la apotema, consulte aquí.

2. Halla el área de la base pentagonal. Supongamos que la longitud de un lado es de 6 cm y la longitud de la apotema es de 7 cm. Introduzca los números en la fórmula:

3. determinar la altura. Establecer la altura del molde es de 10 cm.

4. Multiplica el área de la base pentagonal por la altura. Multiplica el área de la base pentagonal, 105 cm, por la altura, 10 cm, para encontrar el volumen del prisma pentagonal común.

5. Da tu respuesta en unidades cúbicas. La respuesta final es 1050 cm.
Consejos
- Tratar "base" no debe confundirse con "plano base".Un plano base se refiere a la forma bidimensional que es la base del prisma (generalmente la parte superior e inferior).Pero ese plano base puede tener su propia base --- uno de los lados de la forma del plano, sirve para encontrar el área de esa forma.
Artículos sobre el tema. "Calcular el volumen de un prisma"
Оцените, пожалуйста статью
Popular