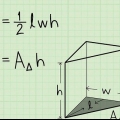
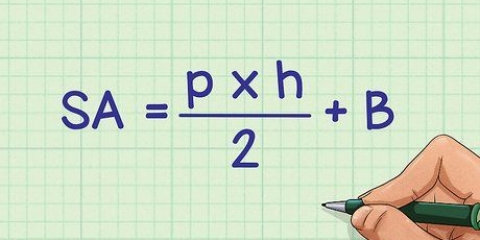En el ejemplo, los lados de la base de la pirámide miden todos 5 cm, y el área de la base se calcula de la siguiente manera: 
Recuerda que las áreas bidimensionales se expresan en cuadrados: centímetros cuadrados, metros, kilómetros, etc. 
En el ejemplo asumimos que la pirámide tiene una altura de 9 cm. En este caso, multiplique el área de la base por este valor, de la siguiente manera: 
Recuerda que los volúmenes se expresan en unidades cúbicas. En este caso, debido a que todas las medidas lineales son centímetros, el volumen se indica en centímetros cúbicos. 
En el ejemplo, divide 225 cm por 3 y la respuesta es 75 cm para el volumen. 


Esta sustitución se ve así: 


 .....(ecuación original)
.....(ecuación original) .....(cuadrar ambos lados)
.....(cuadrar ambos lados) .....(ingresar valores)
.....(ingresar valores) .....(simplificar fracción)
.....(simplificar fracción) .....(simplificar cuadrado)
.....(simplificar cuadrado) .....(sustraer)
.....(sustraer) .....(raíz simplificada)
.....(raíz simplificada)
De los cálculos deducimos que la altura de la pirámide es de 12 cm. Usa esto junto con el lado de 10 cm de la base para calcular el volumen de la pirámide: 









 ..........(ecuación ajustada)
..........(ecuación ajustada) ..........(sustituir h en ambos lados)
..........(sustituir h en ambos lados) ..........(restar la raíz cuadrada de ambos lados)
..........(restar la raíz cuadrada de ambos lados) ..........(llene los números)
..........(llene los números) ..........(simplificar los cuadrados)
..........(simplificar los cuadrados) ..........(restar valores)
..........(restar valores) ..........(simplificar la raíz cuadrada)
..........(simplificar la raíz cuadrada)Duplica este valor para encontrar la diagonal de la base cuadrada de la pirámide. Así, la diagonal de la base de la pirámide es 9,8*2 = 19,6 cm. 
En este ejemplo de pirámide, la diagonal de la base es de 19,6 cm. Por lo tanto, el lado es igual a: 





Calcular el volumen de una pirámide cuadrada
Contenido
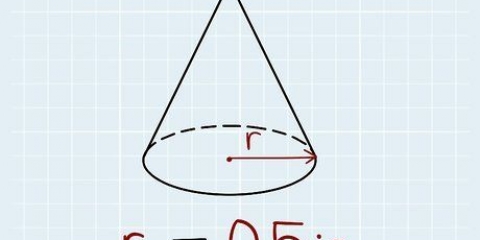
Una pirámide cuadrada es una figura tridimensional con una base cuadrada y triángulos inclinados que se unen en un punto por encima de la base. En caso de que 


Pasos
Método 1 de 3: Determinar el volumen con el área de la base y la altura

1. Mide la longitud del lado de la base. Dado que las pirámides cuadradas por definición tienen una base cuadrada, todos los lados de la base deben tener la misma longitud. Entonces con una pirámide cuadrada solo necesitas saber la longitud de uno de los lados.
- Supongamos que tienes una pirámide con una base cuadrada cuyos lados tienen una longitud de
. Usarás este valor para calcular el área de la base.
- Si los lados de la base no tienen la misma longitud, entonces tienes un pirámide rectangular en lugar de una pirámide cuadrada. La fórmula del volumen de una pirámide rectangular es muy similar a la fórmula de las pirámides cuadradas. En caso de que
es la longitud de la base de la pirámide rectangular y
el ancho, entonces el volumen de la pirámide
.

2. Calcular el área de la base. Para determinar el volumen, primero necesitas el área de la base. Lo haces multiplicando el largo y el ancho de la base. Dado que la base de una pirámide cuadrada es un cuadrado, todos los lados tienen la misma longitud, y el área de la base es igual al cuadrado de la longitud de uno de sus lados (por lo tanto, multiplicado por sí mismo).


3. Multiplica el area de la base por la altura de la piramide. Luego multiplicas el area de la base por la altura de la piramide. Como recordatorio, la altura es la distancia es la longitud del segmento de línea desde la parte superior de la pirámide hasta la base, en ángulo recto.


4. Divide esta respuesta por 3. Finalmente, determinas el volumen de la pirámide dividiendo el valor que acabas de encontrar (multiplicando el área de la base por la altura) por 3. Esto calcula el volumen de la pirámide cuadrada.
Método 2 de 3: determina el volumen con la apotema

1. Mide la apotema de la pirámide. A veces no se da la altura perpendicular de la pirámide (o hay que medirla), sino la apotema. Con la apotema puedes usar el Teorema de pitágoras usar para calcular la altura perpendicular.
- La apotema de una pirámide es la distancia del vértice al centro de uno de los lados de su base. Medida al centro de uno de los lados y no a una de las esquinas de la base. Para este ejemplo asumimos que la apotema es de 13 cm y la longitud de un lado de la base es de 10 cm.
- Recuerda que el Teorema de Pitágoras se puede expresar como la ecuación
, por lo cual
y
los catetos perpendiculares son del triángulo rectángulo y
la hipotenusa.

2. Imagina un triángulo rectángulo. Para usar el teorema de Pitágoras necesitas un triángulo rectángulo. Imagina un triángulo dividiendo la pirámide por la mitad y perpendicular a la base de la pirámide. La apotema de la pirámide, llamada  , es la hipotenusa de este triángulo rectángulo. La base de este triángulo rectángulo es la mitad de la longitud de
, es la hipotenusa de este triángulo rectángulo. La base de este triángulo rectángulo es la mitad de la longitud de  , el lado de la base cuadrada de la pirámide.
, el lado de la base cuadrada de la pirámide.
 , es la hipotenusa de este triángulo rectángulo. La base de este triángulo rectángulo es la mitad de la longitud de
, es la hipotenusa de este triángulo rectángulo. La base de este triángulo rectángulo es la mitad de la longitud de  , el lado de la base cuadrada de la pirámide.
, el lado de la base cuadrada de la pirámide.
3. Asignar variables a los valores. El teorema de Pitágoras usa las variables a, b y c, pero es útil reemplazarlas con variables que sean significativas para su problema. la apotema  toma el lugar de
toma el lugar de  en el teorema de Pitágoras. El cateto del triángulo rectángulo (
en el teorema de Pitágoras. El cateto del triángulo rectángulo ( ), toma el lugar de
), toma el lugar de  vas a la altura
vas a la altura  determinar la pirámide, que ocupa el lugar de
determinar la pirámide, que ocupa el lugar de  en el teorema de Pitágoras.
en el teorema de Pitágoras.
 toma el lugar de
toma el lugar de  en el teorema de Pitágoras. El cateto del triángulo rectángulo (
en el teorema de Pitágoras. El cateto del triángulo rectángulo ( ), toma el lugar de
), toma el lugar de  vas a la altura
vas a la altura  determinar la pirámide, que ocupa el lugar de
determinar la pirámide, que ocupa el lugar de  en el teorema de Pitágoras.
en el teorema de Pitágoras.


4. Usa el teorema de Pitágoras para calcular la altura perpendicular. Utilice los valores medidos  y
y  . Luego resuelve la ecuación:
. Luego resuelve la ecuación:
 y
y  . Luego resuelve la ecuación:
. Luego resuelve la ecuación: .....(ecuación original)
.....(ecuación original) .....(cuadrar ambos lados)
.....(cuadrar ambos lados) .....(ingresar valores)
.....(ingresar valores) .....(simplificar fracción)
.....(simplificar fracción) .....(simplificar cuadrado)
.....(simplificar cuadrado) .....(sustraer)
.....(sustraer) .....(raíz simplificada)
.....(raíz simplificada)
5. Usar la altura y la base para calcular el volumen. Después de aplicar estos cálculos al Teorema de Pitágoras, ahora tienes la información que necesitas para calcular el volumen de la pirámide. Usa la fórmula  y resolverlos, asegurándose de dar la respuesta en unidades cuadradas.
y resolverlos, asegurándose de dar la respuesta en unidades cuadradas.
 y resolverlos, asegurándose de dar la respuesta en unidades cuadradas.
y resolverlos, asegurándose de dar la respuesta en unidades cuadradas.



Método 3 de 3: Determinar el volumen con la altura de las patas

1. Mide la altura de las patas de la pirámide. La altura de las patas es la longitud de las aristas de la pirámide, medida desde la parte superior hasta una de las esquinas de la base. Como arriba, usa el Teorema de Pitágoras para calcular la altura perpendicular de la pirámide.
- En este ejemplo suponemos que la altura de las patas es de 11 cm y que la altura perpendicular es de 5 cm.

2. Imagina un triángulo rectángulo. Nuevamente necesitas un triángulo rectángulo para poder usar el Teorema de Pitágoras. En este caso, sin embargo, el valor desconocido es la base de la pirámide. Conocida es la altura vertical y la altura de las piernas. Ahora imagine cortar la pirámide en diagonal de una esquina a la otra, y luego abrir la figura, el plano resultante se vería como un triángulo. La altura de ese triángulo es la altura perpendicular de la pirámide. Esto divide el triángulo expuesto en dos triángulos rectángulos simétricos. La hipotenusa de cada uno de los triángulos rectángulos es la altura de los catetos de la pirámide. La base de cada uno de los triángulos rectángulos es la mitad de la diagonal de la base de la pirámide.

3. Asignar variables. Usa el triángulo rectángulo imaginario y asigna valores al Teorema de Pitágoras. sabes la altura vertical,  que es un lado del teorema de Pitágoras,
que es un lado del teorema de Pitágoras,  . La altura de las patas de la pirámide,
. La altura de las patas de la pirámide,  forma la hipotenusa de este triángulo rectángulo imaginario, y por lo tanto toma el lugar de
forma la hipotenusa de este triángulo rectángulo imaginario, y por lo tanto toma el lugar de  . La diagonal desconocida de la base de la pirámide es el lado restante del triángulo rectángulo,
. La diagonal desconocida de la base de la pirámide es el lado restante del triángulo rectángulo,  Después de hacer estas sustituciones, la ecuación se ve así:
Después de hacer estas sustituciones, la ecuación se ve así:
 que es un lado del teorema de Pitágoras,
que es un lado del teorema de Pitágoras,  . La altura de las patas de la pirámide,
. La altura de las patas de la pirámide,  forma la hipotenusa de este triángulo rectángulo imaginario, y por lo tanto toma el lugar de
forma la hipotenusa de este triángulo rectángulo imaginario, y por lo tanto toma el lugar de  . La diagonal desconocida de la base de la pirámide es el lado restante del triángulo rectángulo,
. La diagonal desconocida de la base de la pirámide es el lado restante del triángulo rectángulo,  Después de hacer estas sustituciones, la ecuación se ve así:
Después de hacer estas sustituciones, la ecuación se ve así:


4. Calcular la diagonal de la base cuadrada. Tienes que reordenar la ecuación para obtener la variable  aislar, y luego calcular su valor.
aislar, y luego calcular su valor.
 aislar, y luego calcular su valor.
aislar, y luego calcular su valor. ..........(ecuación ajustada)
..........(ecuación ajustada) ..........(sustituir h en ambos lados)
..........(sustituir h en ambos lados) ..........(restar la raíz cuadrada de ambos lados)
..........(restar la raíz cuadrada de ambos lados) ..........(llene los números)
..........(llene los números) ..........(simplificar los cuadrados)
..........(simplificar los cuadrados) ..........(restar valores)
..........(restar valores) ..........(simplificar la raíz cuadrada)
..........(simplificar la raíz cuadrada)
5. Halla el lado de la base de la diagonal. La base de la pirámide es un cuadrado. La diagonal de cada cuadrado es igual a la longitud de uno de sus lados, por raíz cuadrada 2. Y entonces puedes encontrar el lado de un cuadrado dividiendo la diagonal por la raíz cuadrada 2.


6. Calcular el volumen usando el lado y la altura. Regrese a la fórmula original para calcular el volumen usando el lado y la altura perpendicular.




Consejos
- En una pirámide cuadrada, la altura perpendicular, la apotema y la longitud del borde de la base se pueden calcular utilizando el Teorema de Pitágoras.
Artículos sobre el tema. "Calcular el volumen de una pirámide cuadrada"
Оцените, пожалуйста статью
Similar
Popular