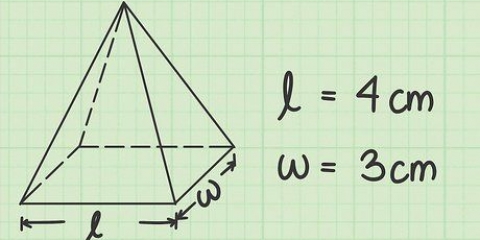Este proceso es básicamente lo mismo que calcular primero el área de la base y luego multiplicar esta área por la altura del cubo (o en otras palabras largo × ancho × alto), porque el área de la base se determina multiplicando el largo por el ancho. Dado que la longitud, el ancho y la altura de un cubo son iguales, podemos simplificar el proceso elevando uno de estos valores a la tercera potencia. Sigamos con nuestro ejemplo. La longitud de la arista era de 2 cm, por lo que el volumen del cubo es 2 x 2 x 2 (o 2)= 8. 
En nuestro ejemplo, la longitud de la costilla se dio en centímetros, por lo que la respuesta debe expresarse en centímetros cubicos. entonces la respuesta es 8cm. 

Así que en nuestro ejemplo dividimos cincuenta por seis: 50/6 = 8,33cm. Recuerda que las unidades de las respuestas bidimensionales se escriben al cuadrado (cm, m, etc.). 
En nuestro ejemplo, √8.33 = 2,89cm. 
Entonces, en nuestro ejemplo: 2.89 × 2.89 × 2.89 = 24,14cm. No olvides escribir la respuesta en unidades cúbicas. 

Esto también se puede deducir del teorema de Pitágoras. D, D y yo forman un triángulo equilátero con D como hipotenusa, entonces D = D + yo. Anteriormente ya habíamos determinado: D = 2yo, por lo que también podemos decir lo siguiente: D = 2yo + yo = 3yo. Supongamos que sabemos que la longitud de la diagonal que va desde una esquina en la base del cubo hasta la esquina opuesta en la cara superior del cubo es de 10 metros. Entonces, si queremos calcular el volumen, ingresamos 10 en la fórmula anterior para D. D = 3yo. 10 = 3yo. 100 = 3yo 33.33 = yo 5.77 metros = yo. A partir de este punto podemos calcular el volumen elevando la longitud de la nervadura al cubo. 5.77 = 192.45 metros
Calcular el volumen de un cubo
Contenido
Un cubo es una figura tridimensional cuya longitud, anchura y altura son iguales. Un cubo tiene seis caras cuadradas, cuyos lados tienen la misma longitud y son perpendiculares entre sí. Calcular el volumen de un cubo es muy simple; por lo general, solo necesita multiplicar lo siguiente: largo × ancho × alto. Debido a que todas las aristas de un cubo tienen la misma longitud, también puedes ver el volumen de un cubo de la siguiente manera: yo, por lo cual yo es la longitud de una de las aristas del cubo. Vaya al paso 1 para una explicación detallada.
Pasos
Método 1 de 3: elevar el borde del cubo al cubo

1. Encuentra la longitud de una de las aristas del cubo. A menudo verá una suma donde ya se da la longitud de una de las costillas. Una vez que tenga esta información, tiene todo lo que necesita para determinar el volumen del cubo. Usa una regla o una cinta métrica si no estás resolviendo un problema matemático, pero solo quieres saber el volumen de un objeto existente en forma de cubo.
- Para comprender mejor el proceso de determinar el volumen de un cubo, comencemos con una suma de ejemplo a medida que avanzamos en los pasos de esta sección. Supongamos que la arista del cubo 2cm largo es. Vamos a utilizar esta información en el siguiente paso para determinar el volumen del cubo.

2. Eleva la longitud de la costilla a la tercera potencia. Una vez que tenga la longitud de una de las costillas, eleve este número a la tercera potencia. En otras palabras, multiplica el número dos veces por sí mismo. Si yo es la longitud de la costilla, entonces multiplicas yo × yo × yo (o en forma más simple yo). El resultado es el volumen del cubo.

3. Exprese su respuesta en unidades cúbicas. El volumen es la medida de un espacio tridimensional, por lo que la solución debe escribirse en unidades cúbicas. En una prueba, puede costarle puntos si no expresa correctamente la respuesta en unidades cúbicas, así que no olvide!
Método 2 de 3: determinar el volumen por área de superficie

1. Encuentra el área de las caras de tu cubo. El más fácil manera de determinar el volumen es elevando la costilla al cubo, pero no es la ningún camino. La longitud de la arista de un cubo o el área de una de sus caras se puede derivar de varias otras propiedades del cubo, lo que significa que si comienzas con esta información puedes determinar el volumen del cubo de forma derivada. Por ejemplo, si solo conoce el área total de todos los lados del cubo, puede encontrar el volumen dividiendo esta área por seis y luego sacando la raíz cuadrada de ese número para encontrar la longitud del borde. A partir de ese punto puedes volver a elevar a la tercera potencia. En esta sección recorremos este proceso paso a paso.
- El area de un cubo esta dada por la formula 6yo, por lo cual yo es la longitud de una de las aristas del cubo. Esta fórmula es en realidad lo mismo que determinar el área bidimensional de uno de los lados del cubo y luego sumar las seis áreas (iguales). Usaremos esta fórmula para determinar el volumen del cubo a partir del área del cubo.
- Supongamos que tenemos un cubo del que sabemos que el área 50cm es, pero no sabemos cuál es la longitud de las costillas. En los próximos pasos usaremos esta información para encontrar el volumen del cubo.

2. Divide el área del cubo entre seis. Como el cubo tiene seis caras de igual área, podemos determinar el área de una cara dividiendo el área del cubo entre seis. El área de un plano es igual a la multiplicación de dos aristas (l × b, b × h, o h × l).

3. Encuentre la raíz cuadrada de este valor. Como el área de una de las caras de un cubo es igual a yo (yo × yo), ahora podemos sacar la raíz cuadrada del valor encontrado para determinar la longitud de una de las nervaduras. Una vez que sepas esto, tienes suficiente información para calcular el volumen del cubo como de costumbre.

4. Eleva este número a la tercera potencia para encontrar el volumen del cubo. Ahora que ha determinado un valor para la longitud de las costillas, puede elevar este número al cubo para determinar el volumen como se describe en la primera sección de este artículo.
Método 3 de 3: determinar el volumen usando diagonales

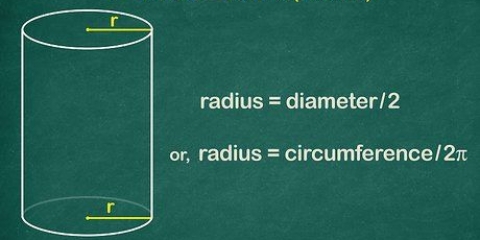
1. Divide la diagonal de una de las caras del cubo por √2 para encontrar la longitud de las aristas del cubo. La diagonal de un cuadrado es √2 × la longitud de una de sus aristas. En otras palabras, si solo conoces el valor de una de las diagonales de una cara del cubo, puedes calcular la longitud de las aristas del cubo dividiendo este valor por √2. Desde ese punto, puede elevar nuevamente a la tercera potencia y determinar el volumen como se describe anteriormente.
- Supongamos que una de las caras del cubo tiene una diagonal de7 metros largo. Entonces podemos calcular la longitud de una de las costillas dividiendo 7 por √2. 7/√2 = 4,96 metros. Ahora que conocemos la longitud de las aristas del cubo, podemos calcular el volumen del cubo elevando 4,96 al cubo: 4,96 = 122,36 metros.
- Prestar atención: D = 2yo, cierto D es la longitud de la diagonal de una de las caras del cubo y yo es la longitud de una de las aristas del cubo. Esto se puede derivar del teorema de Pitágoras, donde el cuadrado de la hipotenusa de un triángulo equilátero es igual a la suma del cuadrado de los otros dos lados. Como la diagonal de una cara de un cubo forma un triángulo equilátero con dos de las aristas de esa cara, podemos decir lo siguiente: D = yo + yo = 2yo.

2. Encuentra el cuadrado de la diagonal entre dos esquinas opuestas del cubo, divide por tres y saca la raíz cuadrada para encontrar la longitud de una de las aristas. Si la longitud de la línea tridimensional entre dos esquinas opuestas del cubo es la única dada, aún puede determinar el volumen del cubo. D forma uno de los lados de un triángulo equilátero cuya hipotenusa es la línea entre dos vértices opuestos del cubo, por lo que podemos decir: D = 3yo, donde D es la línea tridimensional entre dos esquinas opuestas del cubo.
Artículos sobre el tema. "Calcular el volumen de un cubo"
Оцените, пожалуйста статью
Popular