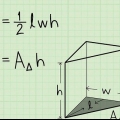
A = 1/2(o)(h) A = 1/2(2)(4) A = 1/2(8) A = 4cm 

Calcular el volumen de una pirámide
Contenido
Para calcular el volumen de una piramide se multiplica el area de la base por la altura de la piramide. Divide el resultado por 3, eso es todo! Lea este artículo con métodos de cálculo para una pirámide con base rectangular y una pirámide con base triangular.
Pasos
Método 1 de 2: pirámide con base rectangular

1. Determinar el largo y el ancho de la base. En este ejemplo, la longitud es de 4 cm y el ancho es de 3 cm. Si tienes una base cuadrada, el método es el mismo, solo el largo y el ancho son iguales. Anota tus medidas.

2. Multiplica el largo por el ancho para calcular el área de la base. Para calcular el área de nuestro ejemplo, multiplicamos 3 cm por 4 cm. 3 cm x 4 cm = 12 cm

3. Multiplica el area de la base por la altura. El área de la base es de 12 cm y la altura de 4 cm, entonces multiplicamos 12 cm por 4 cm. 12 cm x 4 cm = 48 cm

4. Divide el resultado por 3. Eso es lo mismo que multiplicar por 1/3. 48cm/3 = 16cm. El volumen de una pirámide con una altura de 4 cm y una base rectangular con un ancho de 3 cm y una longitud de 4 cm es por lo tanto 16 cm. No olvide indicar el resultado en unidades cúbicas.
Método 2 de 2: pirámide con base triangular

1. Determinar el largo y el ancho de la base. La longitud y el ancho de la base deber perpendiculares entre sí, de lo contrario este método no funcionará. También se pueden ver como la parte inferior y la altura del triángulo. En este ejemplo, el ancho del triángulo es de 2 cm y la longitud es de 4 cm. Escribe esto.

2. Calcular el área de la base. Para calcular el área de la base usamos la siguiente fórmula:A = 1/2(o)(h). Así es como lo hacemos:

3. Multiplica el area de la base por la altura de la piramide. El área de la base es de 4 cm y la altura es de 5 cm. 4 cm x 5 cm = 20 cm.

4. Divide el resultado por 3. 20 cm/3 = 6,67 cm. El volumen de una pirámide con una altura de 5 cm y una base triangular con un ancho de 2 cm y una longitud de 4 cm es por lo tanto 6,67 cm.
Consejos
- En una pirámide de base cuadrada, la altura, la línea que divide el lado triangular en dos triángulos iguales y el ancho de la base están conectados por el teorema de Pitágoras: (ancho ÷ 2) + (alto) = (alto del triángulo)
- Este método también se puede aplicar a objetos como pirámides pentagonales, pirámides hexagonales, etc. El proceso general es: A) calcular el área de la base; B) medir la altura desde la parte superior de la pirámide hasta el centro de la base; C) multiplicar A por B; D) dividir por 3.
- En todo ordinario las pirámides son las nervaduras verticales, la línea que divide el lado triangular en dos triángulos iguales y el ancho de la base conectado por el teorema de Pitágoras: (longitud del lado ÷ 2) + (longitud de la nervadura) = (altura)
Advertencias
- Las pirámides tienen tres tipos de alturas: la línea que divide la cara triangular en dos triángulos iguales, la longitud de la nervadura (a lo largo del lado de una cara triangular) y la altura real (desde la punta de la pirámide perpendicular hasta la base) . ).
Artículos sobre el tema. "Calcular el volumen de una pirámide"
Оцените, пожалуйста статью
Popular