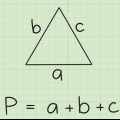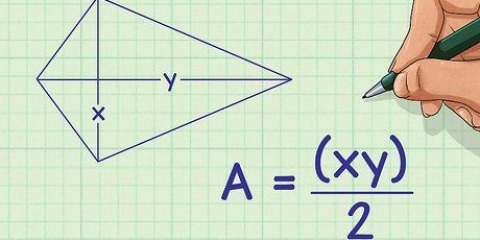Instrucciones de paso a paso gratis 
Área = 1/2 x (3 cm x 5 cm) 
Área = 1/2 x (3 cm x 5 cm) Superficie = 1/2 x 15 cm área = 7.5cm 
Área = √{6 (6 - 3)(6 - 4)(6 - 5)} 
6 - 3 = 3 6 - 4 = 2 6 - 5 = 1 Área = √{6 (3)(2)(1)} 
Área = 1/2(b)(c) x sen A Área = 1/2(150)(231) x sen A 
Área = 1/2(150)(231) x sen A Área = 1/2(34,650) x sen A Área = 17.325 x sen A Área = 17,325 x .8386705 Área = 14.530 cm
Calcular el area de un triangulo
Contenido
Aunque el método más común para calcular el área de un triángulo es multiplicar la mitad de su base por su altura, existen otras formas de calcular el área de un triángulo, según los datos disponibles. Esto incluye la longitud de los tres lados, la longitud de un lado de un triángulo equilátero y la longitud de dos lados junto con el ángulo incluido. Lea aquí cómo puede calcular el área de un triángulo usando estos datos.
Pasos
Método 1 de 4: con la base y la altura
1. Determina la base y la altura de tu triángulo. La base del triángulo es la longitud de un lado, que suele ser el lado inferior del triángulo. La altura es la longitud desde la base hasta la esquina superior del triángulo, que es perpendicular a la base. En un triángulo rectángulo, la base y la altura son los dos lados que se encuentran en un ángulo de 90 grados. Pero, en otro triángulo, como se ve a continuación, la línea de altitud cortará la forma.
- Una vez que haya determinado la base y la altura del triángulo, estará listo para comenzar a usar la fórmula.
2. Escriba la fórmula para encontrar el área de un triángulo. La fórmula para este tipo de problema es Área = 1/2 (base x altura), o 1/2 (sujetador). Una vez que hayas anotado todo, puedes comenzar a completar la longitud de la altura y la base.
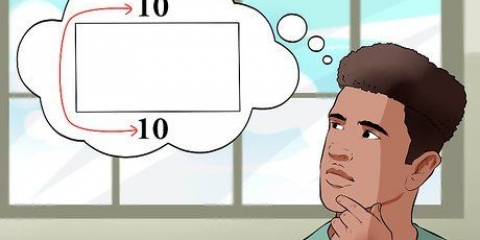
3. Ingrese valores de base y altura. Encuentra la base y la altura del triángulo y usa estos valores en la ecuación. En este ejemplo, la altura del triángulo es de 3 cm y la base del triángulo es de 5 cm. Así es como se vería la fórmula después de ingresar estos valores:
4. Resuelve la ecuación. Puedes multiplicar la altura por la base primero porque esos valores están entre paréntesis. Luego multiplicas el resultado por 1/2. Recuerda que darás la respuesta en metros cuadrados porque estás trabajando en un espacio bidimensional. He aquí cómo resolver esto para la respuesta final:
Método 2 de 4: usar la longitud de cada lado (fórmula de Heron)
1. Calcular el medio perímetro (semiperímetro) del triángulo. Para encontrar el medio perímetro del triángulo todo lo que necesitas hacer es sumar todos los lados y dividir el resultado por dos. La fórmula para encontrar el medio perímetro de un triángulo es la siguiente: semiperímetro = (longitud del lado a + longitud del lado b + longitud del lado c) / 2, o s = (a + b + c) / 2. Dado que se dan las tres longitudes del triángulo rectángulo, 3 cm, 4 cm y 5 cm, puede sustituirlas directamente en las fórmulas y resolver el problema del medio perímetro:
- s = (3 + 4 + 5)/2
- s = 12/2
- s = 6
2. Ingresa los valores correctos en la fórmula para encontrar el área de un triángulo. Esta fórmula para encontrar el área de un triángulo también se llama fórmula de Heron y es así: Área = √{s (s - a)(s - b)(s - c)}. Repetimos el paso anterior donde s la media circunferencia es y a, B, y C los tres lados del triangulo. Haz uso de la siguiente secuencia de operaciones: comienza resolviendo todo lo que está dentro de los paréntesis, luego todo lo que está debajo del signo radical y finalmente la propia raíz cuadrada. Así es como se verá esta fórmula cuando haya ingresado todos los valores conocidos:
3. Resta los valores dentro de los paréntesis. Entonces: 6 - 3, 6 - 4 y 6 - 5. Aquí está el resultado en papel:
4. Multiplicar los resultados de estas operaciones. Multiplica 3 x 2 x 1 para obtener 6 como respuesta. Tienes que multiplicar estos números antes de multiplicarlos por 6 porque están entre paréntesis.
5. Multiplica el resultado anterior por la mitad de la circunferencia. Luego multiplica el resultado, 6, por la mitad de la circunferencia, que también es 6. 6x6 = 36.
6. Calcular la raíz cuadrada. 36 es un cuadrado perfecto y √36 = 6. No olvides la unidad con la que comenzaste -- centímetros. Expresar la respuesta final en centímetros cuadrados. El area del triangulo de lados 3, 4 y 5 es 6 cm.
Método 3 de 4: usar un lado de un triángulo rectangular
1. Halla el lado del triangulo equilatero. Un triángulo equilátero tiene lados de igual longitud y ángulos iguales. Sabes que estás tratando con un triángulo equilátero, ya sea porque es un hecho o porque sabes que todos los ángulos y todos los lados tienen el mismo valor. el valor de uno de los lados de este triangulo es 6 cm. Tenga en cuenta esto.
- Si sabe que está tratando con un triángulo equilátero pero solo se conoce el perímetro, simplemente divida este valor por 3. Por ejemplo, la longitud de un lado de un triángulo equilátero con perímetro 9 es simplemente 9/3, o 3.
2. Escribe la fórmula para encontrar el área de un triángulo equilátero. La fórmula para este tipo de problema es área = (s^2)(√3)/4. Tenga en cuenta que s "seda" significa.
3. Aplicar el valor de un lado a la ecuación. Primero calcula el cuadrado del lado de valor 6, para obtener 36. Luego encuentra el valor de √3, si la respuesta se va a dar en decimales. Ahora ingresa √3 en tu calculadora para obtener 1.732 para obtener. Divide este número por 4. Tenga en cuenta que también puede dividir 36 entre 4 y luego multiplicar por √3; el orden de las operaciones no tiene efecto en la respuesta.
4. Resolver. Ahora todo se reduce principalmente a contar. 36 x √3/4 = 36 x .433 = 15.59 cm El area de un triangulo equilatero de 6 cm de lado es 15.59cm.
Método 4 de 4: usar la longitud de dos lados y el ángulo incluido
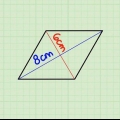
1. Encuentra el valor de las longitudes de dos lados y el ángulo incluido. El ángulo incluido es el ángulo entre los dos lados conocidos del triángulo. Necesitas saber estos valores para encontrar el área de un triángulo usando este método. Supongamos un triángulo con las siguientes dimensiones:
- ángulo A = 123º
- lado b = 150 cm
- lado c = 231 cm
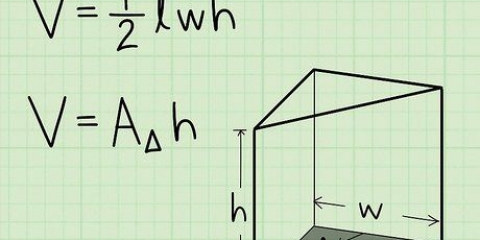
2. Escribe la fórmula para encontrar el área del triángulo. La fórmula para encontrar el área de un triángulo con dos lados conocidos y un ángulo incluido conocido es la siguiente: Área = 1/2(b)(c) x sen A. En esta ecuación representa "B" y "C" las longitudes de los lados y "a" la esquina. Siempre debes tomar el seno del ángulo en esta ecuación.
3. Completa los valores en la ecuación. Así es como se ve la ecuación después de ingresar estos valores:
4. Resolver. Para resolver esta ecuación, primero multiplica los lados y divide el resultado por dos. Luego multiplica este resultado por el seno del ángulo. El valor del seno se puede encontrar con su calculadora. No olvides dar tu respuesta en unidades cúbicas. Así es como se hace:
Consejos
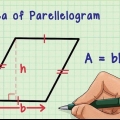
- Si no entiende por qué la fórmula básica de altura funciona de esta manera, aquí hay una breve explicación. Si crea un segundo triángulo idéntico y lo coloca uno al lado del otro, formará un rectángulo (dos triángulos rectángulos) o un paralelogramo (dos triángulos no rectángulos). Para encontrar el área de un rectángulo o paralelogramo solo necesitas multiplicar la base por la altura. Como un triángulo es igual a la mitad de un rectángulo o paralelogramo, se deduce que el área de un triángulo es igual a la mitad de una base por su altura.
Artículos sobre el tema. "Calcular el area de un triangulo"
Оцените, пожалуйста статью
Popular
