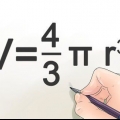Calcular el volumen de un cono: 5 pasos (con fotos)

Contenido

Pasos
- Método 1 de 1: calcular el volumen de un cono
Consejos
Advertencias

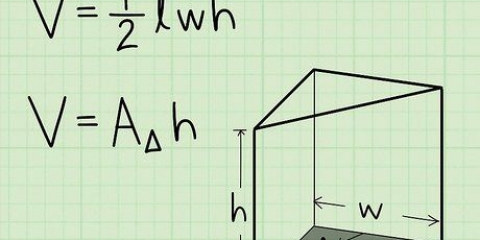
Puedes calcular fácilmente el volumen de un cono si conoces su altura y radio. La fórmula para calcular el volumen es entonces la siguiente: v = hπr/3. A continuación te lo explicamos en sencillos pasos.

Pasos

Método 1 de 1: calcular el volumen de un cono

Imagen titulada Calcular el volumen de un cono Paso 1

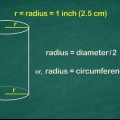
1. Calcular el radio. Si ya conoce el radio, puede omitir este paso e ir directamente al paso 2. Si conoce el diámetro del círculo, todo lo que necesita hacer es dividirlo por dos para calcular el radio. Si conoce la circunferencia, calcula el radio dividiendo la circunferencia por 2π. Y si tú tampoco sabes la circunferencia, solo tienes que agarrar una regla y medir el diámetro. Luego divide el valor medido por dos y tienes el radio. Supongamos que el radio de la base de este cono es de 0,5 cm.

Imagen titulada Calcular el volumen de un cono Paso 2

2. Usa el radio para calcular el área de la base del cono. Para hacer esto, simplemente use la fórmula para calcular el área de un círculo: A = r. En lugar de "r" llenamos 5: A = π(0.5), o pi por 0,5 al cuadrado A = π(0,5) = 0,79 cm .

Imagen titulada Calcular el volumen de un cono Paso 3

3. Mide la altura del cono. Si ya sabes la altura, solo tienes que anotarla. Usa una regla si aún no sabes la altura. Supongamos que la altura de nuestro cono es de 1,5 cm. Nota: siempre debe asegurarse de que la altura se indique en la misma unidad que el radio; en este caso centímetros.

Imagen titulada Calcular el volumen de un cono Paso 4

4. Multiplica el área de la base por la altura del cono. Multiplica 0,79 cm por 1,5 cm. 0,79 cm x 1,5 cm = 1,19 cm.

Imagen titulada Calcular el volumen de un cono Paso 5

5. Dividir el resultado por tres. Divide 1,19 cm entre 3 para calcular el volumen del cono. 1,19 cm/3 = 0,40 cm.

Consejos

Asegúrate de que tus medidas sean exactas.
Así es como funciona:

De hecho, calculas el volumen de un cono primero fingiendo que estás tratando con un cilindro. En ese caso, tomas el área de la base y la multiplicas por la altura del cilindro. Y en un cilindro siempre caben exactamente 3 conos de la misma altura y con la misma superficie de base. entonces si divides el volumen de un cilindro por tres obtienes el volumen de tres conos que caben en el cilindro.

El radio, la altura y la apotema (desde el vértice del cono hasta un punto de la circunferencia) forman un triángulo rectángulo. Entonces podemos aplicar el teorema de Pitágoras a esto.

Utilizar siempre la misma unidad para las distintas medidas.