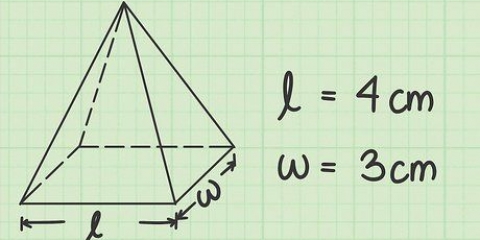Para encontrar s³, multiplique s tres veces por sí mismo: s³ = s x s x s 
Si no está 100% seguro de si su forma es un cubo, mida todos los lados para ver si son iguales. Si no lo son, tendrá que utilizar el siguiente método para calcular el volumen de una viga. Nota: En las imágenes de muestra, las medidas se dan en pulgadas (in), sin embargo, usamos centímetros (cm). 




Ejemplo: La longitud de esta viga es de 4 cm, entonces l = 4 cm. No te preocupes demasiado por qué lado es la longitud, etc. Mientras solo mida tres lados diferentes, el resultado será el mismo. 
Ejemplo: el ancho de esta viga es de 3 cm, entonces b = 3 cm. Si mide la viga con una regla o cinta métrica, no olvide anotar todo en la misma unidad de medida. 
Ejemplo: La altura de esta barra es de 6 cm, entonces h = 6 cm. 
En este ejemplo, l = 4, b = 3 y h = 6. Por lo tanto, el resultado es V = 4 x 3 x 6 = 72. 
Por ejemplo, si las dimensiones de la viga estuvieran en metros, obtendrías l = 2 m, w = 4 m y h = 8 m. El volumen sería entonces 2 m x 4 m x 8 m = 64 m³. 

En la mayoría de los casos es suficiente redondear pi a 3,14. Pregúntale a tu profesor qué quiere. La fórmula para encontrar el volumen de un cilindro en realidad es muy similar a la del volumen de una viga: multiplicas la altura de la forma por el área de la base. Para una viga, el área de la base es l x b, para un cilindro es π x r², el área de un círculo con radio r. 

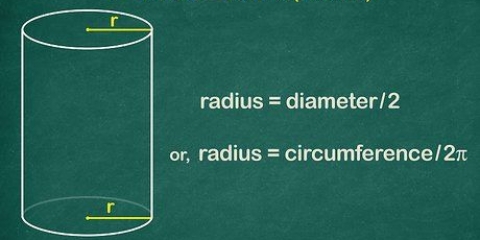
Otra opción es medir la circunferencia del círculo (la distancia alrededor de él) con un trozo de cuerda o una cinta métrica. Luego pon el resultado en esta fórmula: C (circunferencia) es 2 x π x r. Divide la circunferencia por 2 x π (6.28) y tienes el radio. Por ejemplo, si la circunferencia que mediste es de 8 cm, entonces el radio es de 1,27 cm. Si realmente necesita una medida exacta, puede usar cualquier método para ver si los resultados son los mismos. Si no, verifique nuevamente. El método de la circunferencia suele dar un resultado más preciso. 
Si el radio es de 4 cm, entonces el área del círculo es A = π x 4². 4² = 4 x 4, o 16. 16 xπ = 16 x 3,14 = 50,24 cm². Si se conoce el diámetro de la base, en lugar del radio, recuerda que d = 2 x r. Entonces tienes que dividir el diámetro por dos para encontrar el radio. 

V = π x 4² x 10 π x 4²= 50.24 50,24 x 10 = 502,4 V = 502,4 


La fórmula para pirámides rectas, donde el vértice está directamente sobre el centro de la base, es la misma que para pirámides inclinadas, donde el vértice no está en el centro. 
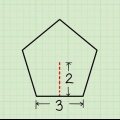
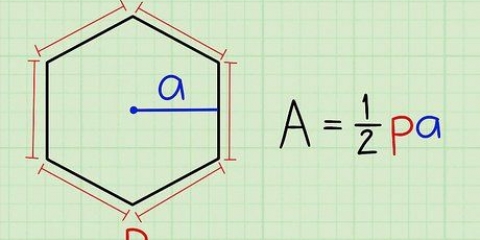
La fórmula del área de un triángulo es A = 1/2 x b x h, donde b es la base y h la altura. Es posible calcular el área de cualquier polígono regular mediante la fórmula A = 1/2 xpxa, donde A es el área, p es el perímetro y a es la apotema, que es la distancia del centro de la forma a el centro de uno de los lados. También puede ponérselo fácil y usar una calculadora de polígonos regulares en línea. 

Si hubiéramos tenido otra pirámide de base con un área de 26 y una altura de 8, el resultado hubiera sido: 1/3 x 26 x 8 = 69,33. 


La parte π x r² se refiere al área del círculo que forma la base del cono. Entonces, la fórmula para el volumen del cono es 1/3 x ancho x alto, al igual que la fórmula para la pirámide en el método anterior! 
En este ejemplo el radio es de 3 cm. Si ponemos eso en la fórmula obtenemos: A = π x 3². 3² = 3 x3, o 9, entonces A = π x 9. A = 28,27 cm². 


En nuestro ejemplo que es 141,35 x 1/3 = 47,12, el volumen del cono. De nuevo: 1/3 x π x 3² x 5 = 47,12. 




Por ejemplo, si mides la pelota y ves que la circunferencia es de 18 cm, divides eso por 6,28, sabes que el radio es de 2,87 cm. Puede ser complicado medir una esfera, por lo que es mejor medirla tres veces y promediarla (sumar las tres medidas y dividir por tres) para obtener la medida lo más precisa posible. Por ejemplo, si midió tres veces y los resultados fueron 18 cm, 17,75 cm y 18,2 cm, súmelos (18 + 17,5 + 18,2 = 53,95) y divídalos por 3 (53,95/3 = 17,98). Usas este promedio cuando calculas el volumen. 


Así que en nuestro ejemplo se convierte en 36 x 3,14 = 113,09. 
Calcular volumen
Contenido
El volumen de una figura es el espacio tridimensional que ocupa la figura. Puede representar el volumen como la cantidad de agua (o aire, arena, etc.).) que encajaría en el molde si estuviera completamente lleno. Las unidades de medida de volumen comúnmente utilizadas son centímetros cúbicos y metros cúbicos.Este artículo le enseñará cómo calcular el volumen de seis formas tridimensionales diferentes que se encuentran comúnmente en las pruebas de matemáticas, incluidos el cubo, la esfera y el cono. Verás que hay muchas similitudes que te serán fáciles de recordar. A ver si puedes encontrar esas coincidencias!
Pasos
Método 1 de 6: calcular el volumen de un cubo

1. reconocer un cubo. Un cubo es una forma tridimensional con seis caras cuadradas idénticas.En otras palabras, es una caja con lados iguales en todas partes.
- Un dado es un buen ejemplo de un cubo que puedes tener en casa. Los cubos de azúcar o los bloques para niños también suelen ser cubos.

2. Aprende la fórmula para calcular el volumen del cubo. Como todas las longitudes de los lados del cubo tienen la misma longitud, la fórmula para calcular el volumen del cubo es muy fácil. El lugar donde se juntan dos lados se llama costilla. Abreviamos volumen a "V". Las costillas, o la longitud del costado, las llamamos aquí "s". La fórmula entonces se convierte en V = s³

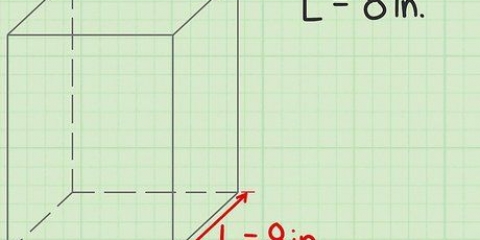
3. Encuentra la longitud de un lado del cubo. Dependiendo de la tarea, es posible que esta información ya esté allí, pero es posible que también deba medirla usted mismo con una regla. Recuerda, como es un cubo, todas las longitudes de los lados deben ser iguales, así que no importa cuál midas.

4. Pon la longitud del lado en la formula V = s³ y calculalo. Por ejemplo, si mides que la longitud del lado de tu cubo es de 5 cm, escribirías la fórmula de la siguiente manera: V = (5)³. 5 x 5 x 5 = 125 cm³, ese es el volumen de tu cubo!

5. Asegúrate de escribir tu respuesta en centímetros cúbicos. En el ejemplo anterior, el cubo se midió en centímetros, por lo que la respuesta debe darse en centímetros cúbicos. Si la longitud del lado del cubo hubiera sido de 3 metros, entonces el volumen habría sido V = (3 m)³ = 27 m³.
Método 2 de 6: calcular el volumen de una viga.

1. Reconocer una viga. Una viga es una figura que consta de seis superficies rectangulares. Así que en realidad es un rectángulo tridimensional, una especie de caja.
- En realidad, un cubo es solo una viga especial, donde todos los lados son iguales.

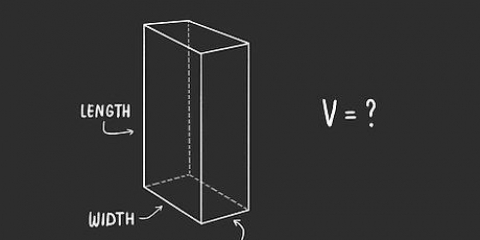
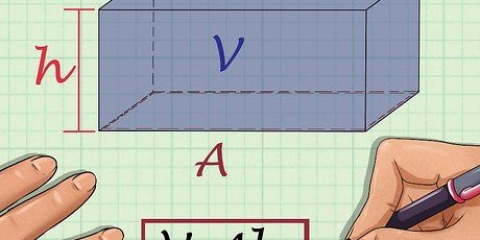
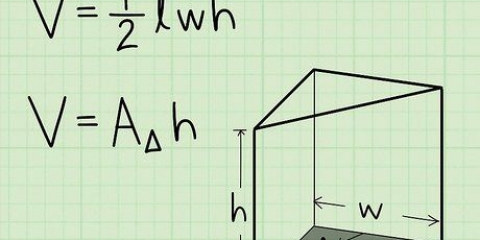
2. Aprende la fórmula para calcular el volumen de una viga. La fórmula para el volumen de una viga es V = largo (largo) x ancho (ancho) x alto (alto), o V = largo x ancho x alto. Nota: Las imágenes que acompañan a estos ejemplos muestran "w" por ancho.

3. Encuentre la longitud de la viga. La longitud es el lado más largo de la viga que es paralelo al suelo o superficie sobre la que descansa. Es posible que la longitud ya esté indicada en la imagen o que deba medirla con una regla.

4. Encuentre el ancho de la viga. El ancho de la viga se puede encontrar midiendo el lado corto que es paralelo al suelo o superficie sobre la que descansa. Nuevamente, primero verifique si ya está indicado en la imagen y, de lo contrario, mídalo con su regla.

5. Encuentre la altura de la viga. La altura es la distancia desde el suelo o la superficie sobre la que descansa la viga hasta la parte superior de la viga. Mira si ya está indicado en la imagen y mídelo de otra manera con tu regla o cinta métrica.

6. Ingrese las dimensiones en la fórmula y calcule. Recuerda que V = l x a x h.

7. Asegúrate de escribir tu respuesta en centímetros cúbicos. El resultado es por lo tanto 72 centímetros cúbicos, o 72 cm³.
Método 3 de 6: calcular el volumen de un cilindro

1. Aprende a identificar un cilindro. Un cilindro es una forma tridimensional con dos extremos redondos idénticos conectados por un solo lado curvo. En realidad es una barra recta y redonda.
- Una lata es un buen ejemplo de un cilindro o una batería AA.

2. Memoriza la fórmula del volumen de un cilindro. Para calcular el volumen de un cilindro, necesitas saber su altura y el radio de su base circular.El radio es la distancia desde el centro del círculo hasta el borde. La fórmula es V =π x r² x h, donde V es el volumen, r es el radio,h es la altura y π es la constante pi.

3. Encuentre el radio de la base. Si ya está indicado en la imagen, solo complételo. Si obtuviste el diámetro en lugar del radio, simplemente divídelo por 2 para encontrar el radio (d = 2 x r).

4. Medir la forma si no se da el radio. Tenga en cuenta que puede ser difícil medir el radio exacto de un círculo. Una opción es medir el círculo en su punto más ancho con la regla de arriba a abajo, dividiéndolo por dos.

5. Calcular el área del círculo en la base. Pon el radio en la fórmula π x r². Multiplica el radio por sí mismo y multiplica ese resultado por π. Por ejemplo:

6. Encuentre la altura del cilindro. Esta es simplemente la distancia entre las dos bases circulares, o la distancia desde la superficie sobre la que descansa el cilindro hasta la parte superior del cilindro. Vea si la longitud ya está indicada en la imagen, o mídala de manera diferente con su regla o cinta métrica.

7. Multiplica el área de la base por la altura del cilindro para encontrar el volumen. Pon los valores en la formula V =π x r² x h. En nuestro ejemplo con un radio de 4 cm y una altura de 10 cm:

8. Recuerda escribir tu respuesta en centímetros cúbicos. En este ejemplo, el cilindro se midió en centímetros, por lo que la respuesta debe escribirse en centímetros cúbicos: V = 502,4 cm³. Si el cilindro se midiera en metros, habría que escribir el volumen en metros cuadrados (m³).
Método 4 de 6: calcular el volumen de una pirámide regular

1. Saber qué es una pirámide regular. Una pirámide es una forma tridimensional con un polígono en la base y lados que se estrechan hacia la parte superior (la punta de la pirámide).Una pirámide regular es una pirámide cuya base es un polígono regular, lo que significa que todos los lados y ángulos de este polígono son iguales.
- Por lo general, una pirámide se representa con una base cuadrada y lados que se estrechan en un punto, pero la base de una pirámide en realidad puede tener 5, 6 o 100 lados!
- Una pirámide con un círculo como base se llama cono, que discutiremos en el siguiente método.

2. Aprende la fórmula para calcular el volumen de la pirámide regular. La fórmula para el volumen de una pirámide regular es V = 1/3 x b x h, donde b es el área de la base y h es la altura de la pirámide, o la distancia vertical desde la base hasta la parte superior.

3. Calcular el área de la base. La fórmula para esto depende del número de lados de la base. En nuestro ejemplo, la base es un cuadrado con lados de 6 cm. Recuerda que la fórmula para calcular el área de un cuadrado es A = s². Entonces con nuestra pirámide que es 6 x 6 = 36 cm².

4. Encuentra la altura de la pirámide. En la mayoría de los casos se indicará en la imagen. En nuestro ejemplo, la altura de la pirámide es de 10 cm.

5. Multiplica el área de la base de la pirámide por la altura, y divide por 3 para encontrar el volumen. Recuerda que la fórmula es V = 1/3 x b x h. En nuestro ejemplo, la pirámide tiene una base con un área de 36 y una altura de 10, por lo que el volumen es 36 x 10 x 1/3 = 120.

6. Recuerda escribir el resultado en unidades cúbicas. Las medidas de la pirámide del ejemplo se dieron en centímetros, por lo que el resultado debe escribirse en centímetros cúbicos, 120 cm³. Si las medidas fueron dadas en metros, escribe la respuesta en metros cúbicos (m³).
Método 5 de 6: calcular el volumen de un cono

1. Aprende cuáles son las propiedades de un cono. Un cono es una forma tridimensional con una base circular y un solo punto en la cara opuesta. Otra forma de ver un cono es que es un tipo especial de pirámide con una base circular.
- Si la punta del cono está directamente sobre el centro de la base, se llama cono recto. Si no está directamente sobre el centro, se llama cono oblicuo. Afortunadamente, la fórmula para calcular el volumen es la misma para ambos tipos de conos.

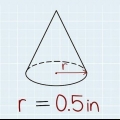
2. Conoce la fórmula para calcular el volumen del cono. Esta fórmula es V = 1/3 x π x r² x h, donde r es el radio del círculo en la base, h es la altura del cono y π es la constante pi, que se puede redondear a 3,14.

3. Calcular el área de la base circular del cono. Para hacer esto, necesita saber el radio de la base, que debe indicarse en su imagen. Si obtuviste el diámetro en lugar del radio, solo divide ese número por 2, porque el diámetro es 2 veces el radio (d = 2 x r). Luego pon el radio en la fórmula A = π x r² para calcular el área.

4. Encuentra la altura del cono. Esta es la distancia vertical desde la base del cono hasta la parte superior. En nuestro ejemplo, la altura del cono es de 5 cm.

5. Multiplica la altura del cono por el área de la base. En nuestro ejemplo, el área de la base es de 28,27 cm² y la altura es de 5 cm, por lo que ancho x alto = 28,27 x 5 = 141,35.

6. Ahora multiplique este resultado por 1/3 (o divida por 3) para obtener el volumen del cono. En el paso anterior, calculamos el volumen de un cilindro, que es un cono donde las paredes estarían verticales y terminarían en otro círculo. Dividirlo por 3 te da el volumen del cono.

7. Recuerda escribir el resultado en unidades cúbicas. Nuestro cono se midió en centímetros, por lo que el volumen debe expresarse en centímetros cúbicos: 47,12 cm³.
Método 6 de 6: calcular el volumen de una esfera

1. reconocer una esfera. Una esfera es una forma tridimensional perfectamente redonda, en la que cada punto de su superficie es equidistante del centro. En otras palabras, es una pelota.

2. Aprende la fórmula para calcular el volumen de una esfera. La fórmula es V = 4/3 x π x r³ (es decir: "cuatro tercios pi por r cúbico"), donde r es el radio de la esfera y π es la constante pi (3.14).

3. Encuentre el radio de la esfera. Si el radio ya está dado en la imagen, es fácil. Dado el diámetro, divida este número por 2 para obtener el radio. El radio de la esfera en este ejemplo es de 3 centímetros.

4. Medir la esfera si no se da el radio. Si necesita medir una esfera (como una pelota de tenis) para encontrar el radio, busque una cuerda lo suficientemente larga como para envolverla por completo. Luego envuélvalo alrededor del objeto en el punto más ancho y marque el punto donde la cuerda se vuelve a unir. Luego mide esta parte de la cuerda con una regla para saber la circunferencia de la esfera. Divida eso por 2 x π, o 6.28, entonces sabrá el radio.

5. Eleva el radio a la tercera potencia para encontrar r³. Elevar a la tercera potencia simplemente significa multiplicar el número tres veces por sí mismo, entonces r³ = r x r x r. En nuestro ejemplo r=3 que se convierte en 3 x 3 x 3 = 27.

6. Multiplica tu respuesta por 4/3. Puedes hacerlo con una calculadora, o simplemente hacerlo tú mismo y simplificar la fracción. En nuestro ejemplo es 27 x 4/3 = 180/3, o 36.

7. Multiplica el resultado por π para encontrar el volumen de la esfera. El último paso para calcular el volumen es multiplicar el resultado hasta ahora por π. Redondea π a dos decimales, eso es suficiente para la mayoría de los problemas de matemáticas (a menos que tu profesor diga lo contrario), así que multiplícalo por 3,14 y obtendrás tu respuesta.

8. Escribe tu respuesta en unidades cubicas. En nuestro ejemplo, medimos en centímetros, por lo que la respuesta es V = 113,09 cm³.
Artículos sobre el tema. "Calcular volumen"
Оцените, пожалуйста статью
Popular