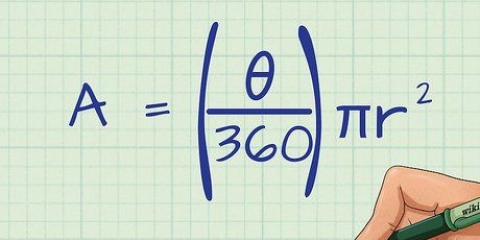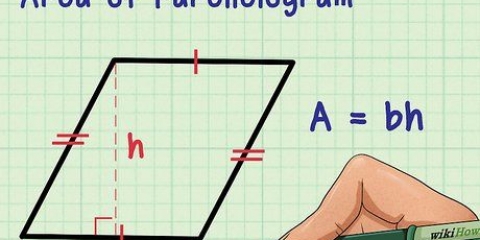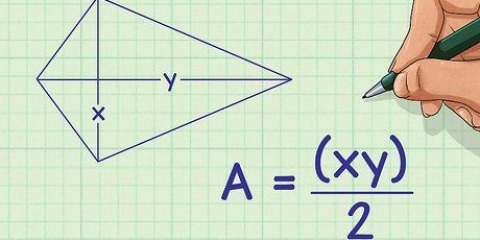Ver la apotema como el "x√3"-lado de un triangulo 30-60-90. Puedes verlo así porque el hexágono consta de seis triángulos equiláteros. La apotema corta uno de estos triángulos por la mitad, creando un triángulo con ángulos de 30, 60 y 90 grados. Sabes que el lado opuesto al ángulo de 60 grados tiene una longitud de x√3, el lado opuesto al ángulo de 30 grados tiene una longitud de x y el lado opuesto al ángulo de 90 grados tiene una longitud de 2x. Si 10√3 representa "x√3," entonces sabes que x = 10. sabes que x es la mitad de la longitud de la base del triangulo. Duplique esto para determinar la longitud total. entonces la base del triangulo es 20. Hay seis de estos lados en el hexágono, así que para encontrar el perímetro del hexágono multiplicamos 20 por 6 = 120. 
Área = 1/2 x 120 x 10√3 Área = 60x10√3 Área = 600√3 


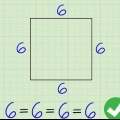
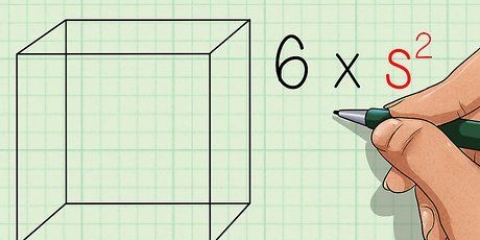
Si tienes un cuadrado con lados de longitud 6, entonces el área es 6 x 6 = 36. 
Si la base de un rectángulo es 4 y la altura es 3, entonces el área es 4 x 3 = 12. 
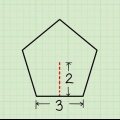
Suponga que tiene un trapezoide cuyas bases tienen longitudes de 6 y 8 y cuya altura es de 10. Entonces el área es [(6 + 8) x 10]/2, que se puede simplificar a (14 x 10)/2 o 140/2, que es un área de 70. 





Calcular el área de un polígono
Contenido
Calcular el área de un polígono puede ser muy sencillo cuando se trata de un triángulo regular. Pero se vuelve mucho más difícil cuando se trata de una forma irregular con once lados. Si quieres saber cómo calcular el área de diferentes polígonos, sigue estos pasos.
Pasos
Parte 1 de 3: Calcular el área de polígonos usando la apotema

1. Escribe la fórmula para hallar el área de un polígono regular. Para encontrar el área de un polígono regular, todo lo que necesitas hacer es seguir la fórmula: área = 1/2 x perímetro x apotema. Eso significa lo siguiente:
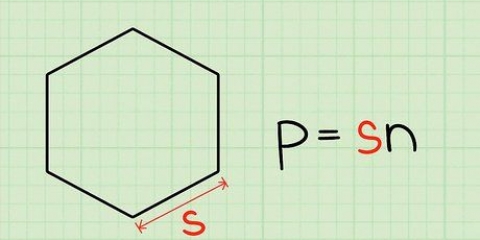
- Circunferencia = la suma de las longitudes de todos los lados
- Apotema = el segmento y también la distancia del centro del polígono al centro de un lado

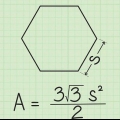
2. Determinar la apotema del polígono. Si usa el método de la apotema, la apotema siempre será un dado. Suponga que está trabajando con un hexágono cuya apotema tiene una longitud de 10√3.

3. Determinar el perímetro del polígono. Si la circunferencia es un hecho, ya casi has terminado. Pero probablemente solo la apotema es un hecho. Si sabes que es un polígono regular, puedes usar la apotema para determinar su perímetro. Así es como haces eso:

4. Ahora podemos poner la apotema y el perímetro en la fórmula. Una vez más: área = 1/2 x perímetro x apotema, el perímetro es 120 y la apotema es 10√3. Entonces la fórmula queda así:

5. simplifica tu respuesta. Tal vez deberías escribir el resultado en decimales en lugar de un radical. Usa tu calculadora para encontrar la raíz cuadrada aproximada de tres y multiplícala por 600. √3 x 600 = 1,039.2. ese es el resultado en decimales.
Parte 2 de 3: Encontrar el área de un polígono regular usando otras fórmulas

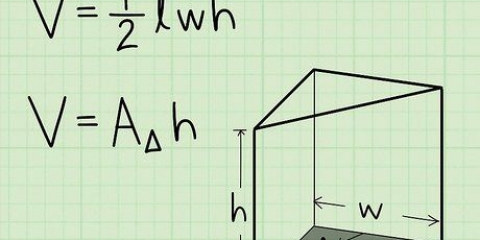
1. Calcular el area de un triangulo par. Si quieres encontrar el área de un triángulo regular puedes usar esta fórmula: área = 1/2 x base x altura.
- Si tienes un triángulo con una base de 10 y una altura de 8, entonces el área = 1/2 x 8 x 10 = 40.

2. Calcular el área de un cuadrado. Para hallar el área de un cuadrado todo lo que necesitas hacer es multiplicar uno de sus lados por sí mismo, ya que la base y la altura son iguales para un cuadrado.

3. Calcular el área de un rectángulo. Para encontrar el área de un rectángulo solo necesitas multiplicar su base por su altura.

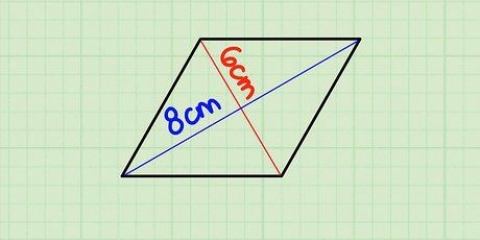
4.Calcular el área de un trapecio. Para encontrar el área de un trapezoide, puedes usar la siguiente fórmula: área = [(base 1 + base 2) x altura]/2.
Parte 3 de 3: encontrar el área de un polígono irregular

1. Usa las coordenadas de los nodos para calcular el área. Si conoces las coordenadas puedes calcular el área de un polígono irregular.

2. Crear una secuencia. Enumere las coordenadas x e y de cada vértice del polígono, en sentido contrario a las agujas del reloj. Repita las coordenadas del primer punto en la parte inferior de la lista.

3. Multiplica la coordenada x de cada vértice por la coordenada y del siguiente vértice. suma los resultados. La suma de estos productos es 82.

4. Multiplica la coordenada y de cada vértice por la coordenada x del siguiente vértice. suma los resultados. La suma de estos productos es -38.

5. Reste la suma de los productos calculados en el paso 4 de la suma de los productos calculados en el paso 3. (82) - (-38) = 120.

6. Divide este resultado por 2 para encontrar el área del polígono. Área = 120/2 = 60.
Consejos
- Si enumera los puntos en el sentido de las agujas del reloj en lugar de en el sentido contrario, también obtiene el área, pero negativa. Por ejemplo, puede usar esto como una herramienta para determinar la secuencia cíclica de un conjunto de puntos que forman un polígono.
- Esta fórmula calcula el área con orientación. Si lo usa en una forma donde dos de las líneas se cruzan como en un 8, obtiene el área en el sentido contrario a las agujas del reloj menos el área en el sentido de las agujas del reloj.
Artículos sobre el tema. "Calcular el área de un polígono"
Оцените, пожалуйста статью
Popular