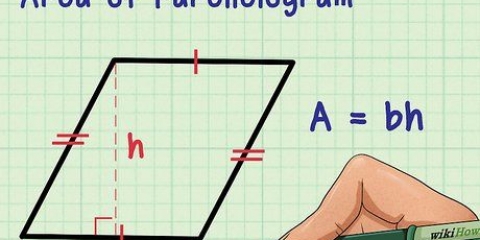La fórmula para calcular la longitud de la apotema es la siguiente: la longitud del lado (s) dividido por 2 veces la tangente (tan) de 180 grados, dividido por el número de lados (norte). 

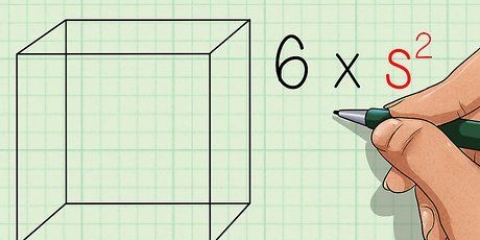
El perímetro es 6 x 10 (norte X s) es igual a 60 (entonces pags = 60). La apotema se calcula reemplazando 6 y 10 para el norte y s de la fórmula. El resultado de 2tan(180/6) es 1,1547, y luego dividimos 10 entre 1,1547, lo que da como resultado 8,66. El área del polígono es a = a X pags / 2 o 8,66 multiplicado por 60 dividido por 2. La solución es un área de 259.8. Tenga en cuenta que no hay paréntesis en el "superficie"-ecuación, entonces 8.66 dividido por 2 multiplicado por 60 da el mismo resultado, al igual que 60 dividido por 2 multiplicado por 8.66. 


Encontrar el área de polígonos regulares
Contenido
Un polígono regular es una figura bidimensional convexa con lados congruentes y ángulos iguales. Para muchos polígonos, como cuadriláteros o triangulos Existen fórmulas simples para encontrar su área, pero si se trata de un polígono, probablemente sea mejor elegir una fórmula que use la apotema y el perímetro de la forma. Con un poco de esfuerzo puedes encontrar el área de polígonos regulares en tan solo unos minutos.
Pasos
Parte 1 de 2: calcular el perímetro

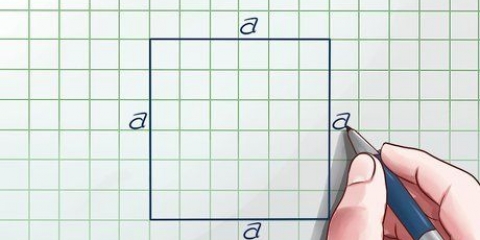
1. Calcular la circunferencia. El perímetro es la longitud combinada del perímetro de una figura bidimensional. Para un polígono regular, esto se puede calcular multiplicando la longitud de un lado por el número de lados (norte) de la figura.

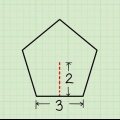
2. Determinar la apotema. La apotema de un polígono regular es la distancia más corta desde su centro a cada lado, formando un ángulo recto. Esto es un poco más difícil de determinar que la circunferencia.

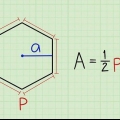
3. Conoce la fórmula correcta. El área de un polígono regular viene dada por la fórmula:área = (a X pags)/2,por lo cual a es la longitud de la apotema, y pags el perímetro del polígono.

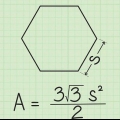
4. Introduzca los valores dea y pags en la fórmula para calcular el perímetro. Como ejemplo, tomemos un hexágono (6 lados) con una longitud de 10 por cada lado (s).
Parte 2 de 2: Comprender los conceptos de una manera diferente

1. Un polígono regular se puede considerar como una colección de triángulos. Cada lado representa la base de un triángulo, y hay tantos triángulos en el polígono como lados. Cada uno de los triángulos son iguales en base, altura y área.

2. Usa la formula para el area de un triangulo. El área de un triángulo es 1/2 de la longitud de su base (que es igual a un lado de un polígono), multiplicada por su altura (que es lo mismo que la apotema de un polígono regular).

3. Note las similitudes. Nuevamente, la fórmula para un polígono regular es 1/2 veces la apotema multiplicada por el perímetro. El perímetro es la longitud de un lado multiplicada por el número de lados (norte); en un polígono regular representa norte también el número de triángulos que forman la figura. Entonces la fórmula no es más que el área de un triángulo multiplicado por el número de triángulos en el polígono.
Consejos
- Consulte wikiHow para obtener más información sobre cómo trabajar con raíces cuadradas y raíces cúbicas.
- Si el dibujo de su octágono (o cualquier forma) está dividido en triángulos y el área de un triángulo está etiquetada, entonces ya no necesita la apotema. Simplemente tome el área de ese triángulo y multiplíquelo por el número de lados en el polígono original.
Artículos sobre el tema. "Encontrar el área de polígonos regulares"
Оцените, пожалуйста статью
Similar
Popular