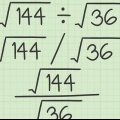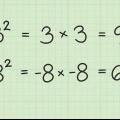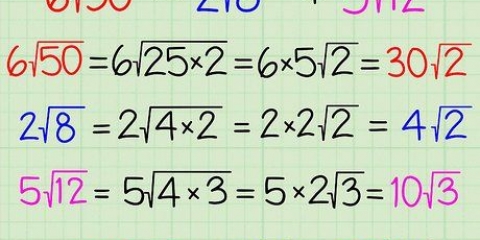Multiplicar raíces cuadradas: 8 pasos (con fotos)

Contenido

Pasos
- Método 1 de 2: Multiplicar raíces cuadradas sin coeficientes
- Método 2 de 2: multiplicar raíces cuadradas con coeficientes
Consejos
Artículos de primera necesidad

Al igual que multiplicar números enteros, también puede multiplicar raíces cuadradas (una ecuación de raíz cuadrada) juntas. A veces, las raíces cuadradas tienen coeficientes (un número entero antes del radical), pero esto solo agrega un paso a la multiplicación y no cambia el proceso. La parte más complicada de la multiplicación de raíces cuadradas es simplificar la expresión para obtener la respuesta final, pero incluso este paso es fácil si conoces tus cuadrados perfectos.

Pasos

Método 1 de 2: Multiplicar raíces cuadradas sin coeficientes

Imagen titulada Multiplicar raíces cuadradas Paso 1

1. Multiplicar las raíces juntas. Un radicando (inglés) es un número debajo del radical. Multiplica raíces de la misma manera que números enteros. Asegúrese de que el producto permanezca debajo del signo radical.

Por ejemplo, si calculas $\sqrt{15} \times \sqrt{5}$ ${sqrt{15}}veces {sqrt{5}}$ , entonces obtienes $15 \times 5 = 75$ $15veces 5=75$ . entonces, $\sqrt{15} \times \sqrt{5} = \sqrt{75}$ ${sqrt{15}}times {sqrt{5}}={sqrt{75}}$ .

Imagen titulada Multiplicar raíces cuadradas Paso 2

2. Derive cualquier cuadrado perfecto a partir de la raíz cuadrada. Para ello, compruebe si un cuadrado perfecto es un factor del número bajo el radical. Si no puede derivar un cuadrado perfecto, su respuesta ya se ha simplificado y no necesita hacer nada más.

Un cuadrado perfecto es el resultado de multiplicar un número (entero positivo o negativo) por sí mismo. Por ejemplo: 25 es un cuadrado perfecto porque

5 \times 5 = 25

$5veces 5=25$ .

Por ejemplo,

\sqrt{75}

${sqrt{75}}$ se puede factorizar en el cuadrado perfecto 25:

\sqrt{75}

${sqrt{75}}$
=

\sqrt{25 \times 3}

${sqrt{25times 3}}$

Imagen titulada Multiplicar raíces cuadradas Paso 3

3. Coloca la raíz cuadrada antes del radical. Deja el otro factor debajo del radical. Ahora tienes la expresión simplificada.

Por ejemplo,

\sqrt{75}

${sqrt{75}}$ se puede disolver en

\sqrt{25 \times 3}

${sqrt{25times 3}}$ , para la raíz cuadrada de 25 (que es 5):

\sqrt{75}

${sqrt{75}}$
=

\sqrt{25 \times 3}

${sqrt{25times 3}}$
=

5 \sqrt{3}

$5{sqrt{3}}$

Imagen titulada Multiplicar raíces cuadradas Paso 4

4. Calcular el cuadrado de una raíz cuadrada. En algunos casos necesitas multiplicar una raíz cuadrada por sí misma. Elevar al cuadrado un número y sacar la raíz cuadrada de un número son operaciones opuestas; asi se deshacen el uno al otro. El resultado del cuadrado de una raíz cuadrada es simplemente el número debajo del radical.

Por ejemplo,

\sqrt{25} \times \sqrt{25} = 25

${sqrt{25}}times {sqrt{25}}=25$ . Obtienes este resultado porque

\sqrt{25} \times \sqrt{25} = 5 \times 5 = 25

${sqrt{25}}times {sqrt{25}}=5times 5=25$ .

Método 2 de 2: multiplicar raíces cuadradas con coeficientes

Imagen titulada Multiplicar raíces cuadradas Paso 5

1. Multiplica los coeficientes. Un coeficiente es un número para el radical. Simplemente ignore el radical y el número debajo de él, y multiplique los dos enteros juntos. Coloque su producto antes del primer radical.

Cuidado con los signos más y menos al multiplicar coeficientes. Recuerda que un número negativo multiplicado por un número positivo produce un resultado negativo, y un número negativo multiplicado por un número negativo produce un resultado positivo.
Por ejemplo, al calcular $3 \sqrt{2} \times 2 \sqrt{6}$ $3{sqrt{2}}veces 2{sqrt{6}}$ , calcular primero $3 \times 2 = 6$ $3veces 2=6$ . Ahora la tarea es la siguiente: $6 \sqrt{2} \times \sqrt{6}$ $6{sqrt{2}}times {sqrt{6}}$ .

Imagen titulada Multiplicar raíces cuadradas Paso 6

2. Multiplica los números debajo de los radicales. Para ello, multiplica los números como si fueran enteros. Asegúrese de que el producto permanezca bajo el signo radical.

Por ejemplo, para una declaración como

6 \sqrt{2} \times \sqrt{6}

$6{sqrt{2}}times {sqrt{6}}$ , calcular el producto de los números debajo de los radicales usando

2 \times 6 = 12

$2veces 6=12$ , de modo que

\sqrt{2} \times \sqrt{6} = \sqrt{12}

${sqrt{2}}times {sqrt{6}}={sqrt{12}}$ . La tarea ahora se ve así:

6 \sqrt{12}

$6{sqrt{12}}$ .

Imagen titulada Multiplicar raíces cuadradas Paso 7

3. Si es posible, factorice cualquier cuadrado bajo el signo radical. Necesitas hacer esto para simplificar tu respuesta. Si no puede resolver un cuadrado, su respuesta ya se ha simplificado y puede omitir este paso.

Un cuadrado es el resultado de multiplicar un número entero (positivo o negativo) por sí mismo. Por ejemplo: 4 es un cuadrado, porque

2 \times 2 = 4

$2veces 2=4$ .

Por ejemplo:

\sqrt{12}

${ sqrt{12}}$ se puede factorizar para que el cuadrado de 4 se coloque antes del radical:

\sqrt{12}

${ sqrt{12}}$
=

\sqrt{4 \times 3}

${sqrt{4veces 3}}$

Imagen titulada Multiplicar raíces cuadradas Paso 8

4. Multiplica la raíz del cuadrado por el coeficiente. Deja el otro factor debajo del radical. Esto produce una expresión simplificada.

Por ejemplo,

6 \sqrt{12}

$6{sqrt{12}}$ se puede disolver en

6 \sqrt{4 \times 3}

$6{sqrt{4veces 3}}$ , después de lo cual puedes sacar la raíz cuadrada de 4 (es decir, 2) y luego multiplicas esto por 6:

6 \sqrt{12}

$6{sqrt{12}}$
=

6 \sqrt{4 \times 3}

$6{sqrt{4veces 3}}$
=

6 \times 2 \sqrt{3}

$6veces 2{sqrt{3}}$
=

12 \sqrt{3}

$12{sqrt{3}}$

Consejos

Conozca sus cuadrados, porque eso hace que este proceso sea mucho más fácil!
Siga las reglas habituales para el signo de un número para determinar si el nuevo coeficiente será positivo o negativo. Un coeficiente positivo multiplicado por un coeficiente negativo da como resultado un número negativo. Dos coeficientes positivos multiplicados juntos o dos coeficientes negativos multiplicados juntos dan un número positivo.
Todos los términos bajo el radical son siempre positivos, así que no tienes que preocuparte por el signo al multiplicar números bajo un radical.