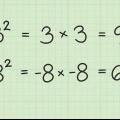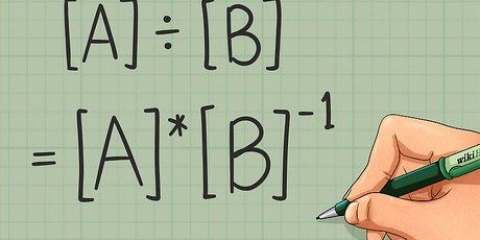Dividir raíces cuadradas

Contenido

Pasos
Consejos
Advertencias

Dividir por raíces cuadradas es esencialmente la simplificación de una fracción. Por supuesto, la presencia de raíces cuadradas hace que el proceso sea un poco más complicado, pero existen reglas que nos permiten trabajar con fracciones de una manera relativamente fácil. Lo más importante que debe recordar es que debe dividir coeficientes por coeficientes y raíces por raíces. Tampoco debes dejar nunca una raíz cuadrada en un denominador.

Pasos

Método 1 de 4: compartir zanahorias

Imagen titulada Dividir raíces cuadradas Paso 1

1. Establecer la fracción. Si la expresión no está ya en forma de fracción, reescríbela así. Esto facilita seguir todos los pasos necesarios para dividir por una raíz cuadrada. Recuerda que un carácter de división es lo mismo que una barra de fracción.

Por ejemplo, si usted $\sqrt{144} \div \sqrt{36}$ ${sqrt{144}}div {sqrt{36}}$ calcula, luego reescribe el problema como: $\frac{\sqrt{144}}{\sqrt{36}}$ ${frac{{sqrt{144}}}{{sqrt{36}}}}$ .

Imagen titulada Dividir raíces cuadradas Paso 2

2. Usa un signo radical. Si su problema tiene una raíz cuadrada en el numerador y el denominador, puede colocar ambas raíces bajo un radical. (Una raíz es el número bajo el radical.) Esto hace que simplificar sea aún más fácil.

Por ejemplo,

\frac{\sqrt{144}}{\sqrt{36}}

${frac{{sqrt{144}}}{{sqrt{36}}}}$ se puede reescribir como

\sqrt{\frac{144}{36}}

${sqrt{{frac{144}{36}}}}$ .

Imagen titulada Dividir raíces cuadradas Paso 3

3. dividir las raíces. Divide los números como lo harías con cualquier número entero. Asegúrate de colocar el cociente debajo de un nuevo radical.

Por ejemplo,

\frac{144}{36} = 4

${frac{144}{36}}=4$ , Entonces

\sqrt{\frac{144}{36}} = \sqrt{4}

${raíz cuadrada{{frac{144}{36}}}}={raíz cuadrada{4}}$ .

Imagen titulada Dividir raíces cuadradas Paso 4

4. Simplificar, Si necesario. Si la raíz del número es un cuadrado, o si uno de los factores es un cuadrado perfecto, entonces necesitas simplificar la expresión. Un cuadrado o cuadrado perfecto es el producto de un número entero multiplicado por sí mismo. Por ejemplo, 25 es un cuadrado perfecto porque

5 \times 5 = 25

$5veces 5=25$ .

Por ejemplo, 4 es un cuadrado perfecto porque

2 \times 2 = 4

$2veces 2=4$ . Por lo tanto:

\sqrt{4}

${ sqrt{4}}$

= \sqrt{2 \times 2}

$={raíz cuadrada{2veces 2}}$

= 2

$=2$
entonces,

\frac{\sqrt{144}}{\sqrt{36}} = \sqrt{4} = 2

${frac{{sqrt{144}}}{{sqrt{36}}}}={sqrt{4}}=2$ .

Método 2 de 4: factorización de raíces

Imagen titulada Dividir raíces cuadradas Paso 5

1. Expresar el problema como una fracción. La expresión probablemente ya esté escrita de esta manera. Si no, cámbialo. Convertirlo en una fracción hace que los pasos necesarios sean más fáciles de seguir, especialmente cuando se factorizan raíces cuadradas. Recuerda que un carácter de división es lo mismo que una barra de fracción.

Por ejemplo, al calcular $\sqrt{8} \div \sqrt{36}$ ${sqrt{8}}div {sqrt{36}}$ , reescribe la expresión como: $\frac{\sqrt{8}}{\sqrt{36}}$ ${frac{{sqrt{8}}}{{sqrt{36}}}}$ .

Imagen titulada Dividir raíces cuadradas Paso 6

2. Factoriza cada zanahoria en factores. Factoriza el número como lo harías con un número entero. Deja los factores bajo los signos radicales.

Por ejemplo:

\frac{\sqrt{8}}{\sqrt{36}} = \frac{\sqrt{2 \times 2 \times 2}}{\sqrt{6 \times 6}}

${frac{{sqrt{8}}}{{sqrt{36}}}}={frac{{sqrt{2times 2times 2}}}{{sqrt{6times 6 }}}}$

Imagen titulada Dividir raíces cuadradas Paso 7

3. Simplifica el numerador y el denominador de la fracción. A para simplificar una raíz cuadrada, ¿Excluye todos los factores cuyo producto es un cuadrado?. Un cuadrado es el resultado de un número entero multiplicado por sí mismo. El factor ahora se convierte en un coeficiente fuera de la raíz cuadrada.

Por ejemplo:

\sqrt{} 2 \times 2 \times 2 \sqrt{6 \times 6}

${frac{{sqrt{{cancel{2times 2times }}2}}}{{sqrt{{cancel{6times 6}}}}}}}$

2 \sqrt{2} 6

${frac{2{sqrt{2}}}{6}}$
entonces,

\frac{\sqrt{8}}{\sqrt{36}} = 2 \sqrt{2} 6

${frac{{sqrt{8}}}{{sqrt{36}}}}={frac{2{sqrt{2}}}{6}}$

Imagen titulada Dividir raíces cuadradas Paso 8

4. Eliminar el signo radical del denominador, si es necesario. Como regla general, una expresión no puede tener una raíz cuadrada en el denominador. Si tu fracción tiene una raíz cuadrada en el denominador, debes eliminarla. Esto significa eliminar la raíz en el denominador. Para ello, multiplica el numerador y el denominador de la fracción por la raíz cuadrada que necesitas eliminar.

Por ejemplo, suponga que su expresión es

6 \sqrt{2} \sqrt{3}

${frac{6{sqrt{2}}}{{sqrt{3}}}}$ , entonces tienes que multiplicar el numerador y el denominador por

\sqrt{3}

${ sqrt{3}}$ para quitar la raíz cuadrada del denominador:

6 \sqrt{2} \sqrt{3} \times \frac{\sqrt{3}}{\sqrt{3}}

${frac{6{sqrt{2}}}{{sqrt{3}}}}times {frac{{sqrt{3}}}{{sqrt{3}}}}$

= 6 \sqrt{2} \times \sqrt{3} \sqrt{3} \times \sqrt{3}

$={frac{6{sqrt{2}}times {sqrt{3}}}{{sqrt{3}}times {sqrt{3}}}}$

= 6 \sqrt{6} \sqrt{9}

$={frac{6{sqrt{6}}}{{sqrt{9}}}}$

= 6 \sqrt{6} 3

$={frac{6{sqrt{6}}}{3}}$ .

Imagen titulada Dividir raíces cuadradas Paso 9

5. Simplifique aún más, si es necesario. A veces te quedan coeficientes que se pueden simplificar aún más, o reducir. Simplifica los números enteros en el numerador y el denominador tal como simplificarías una fracción.

Por ejemplo,

\frac{2}{6}

${frac{2}{6}}$ se puede reducir a

\frac{1}{3}

${frac{1}{3}}$ , Entonces

2 \sqrt{2} 6

${frac{2{sqrt{2}}}{6}}$ se puede reducir a

1 \sqrt{2} 3

${frac{1{sqrt{2}}}{3}}$ , o simplemente

\frac{\sqrt{2}}{3}

${frac{{sqrt{2}}}{3}}$ .

Método 3 de 4: dividir raíces cuadradas con coeficientes

Imagen titulada Dividir raíces cuadradas Paso 10

1. Simplifica los coeficientes. Estos son los números fuera del radical. Para simplificarlos, comparte o reducir, ignora las raíces cuadradas por ahora.

Por ejemplo, si usted $4 \sqrt{32} 6 \sqrt{dieciséis}$ ${frac{4{sqrt{32}}}{6{sqrt{16}}}}$ tienes que calcular, luego simplificas primero $\frac{4}{6}$ ${frac{4}{6}}$ . El numerador y el denominador se pueden dividir por un factor de 2. Entonces puedes simplificar esto a: $\frac{4}{6} = \frac{2}{3}$ ${frac{4}{6}}={frac{2}{3}}$ .

Imagen titulada Dividir raíces cuadradas Paso 11

2. simplificar las raices cuadradas. Si el numerador es divisible por el denominador, simplemente divida los números debajo de los radicales. Si no, simplifica cada raíz cuadrada de la misma manera que otras raíces cuadradas.

Por ejemplo, como 32 es divisible por 16, puedes dividir las raíces cuadradas:

\sqrt{\frac{32}{dieciséis}} = \sqrt{2}

${raíz cuadrada{{frac{32}{16}}}}={raíz cuadrada{2}}$ .

Imagen titulada Dividir raíces cuadradas Paso 12

3. Multiplique los coeficientes simplificados por la raíz cuadrada simplificada. Recuerda que no puede haber una raíz cuadrada en un denominador, así que al multiplicar una fracción por una raíz cuadrada, pones la raíz cuadrada en el numerador.

Por ejemplo,

\frac{2}{3} \times \sqrt{2} = 2 \sqrt{2} 3

${frac{2}{3}}times {sqrt{2}}={frac{2{sqrt{2}}}{3}}$ .

Imagen titulada Dividir raíces cuadradas Paso 13

4. Eliminar la raíz cuadrada en el denominador, si es necesario. Esto se llama racionalización del denominador. La regla es que una expresión no puede tener una raíz cuadrada en el denominador. Para restar la raíz del denominador, multiplica el numerador y el denominador por la raíz cuadrada que deseas restar.

Por ejemplo, si tienes una expresión como

4 \sqrt{3} 2 \sqrt{7}

${frac{4{sqrt{3}}}{2{sqrt{7}}}}$ , entonces tienes que multiplicar el numerador y el denominador por

\sqrt{7}

${ sqrt{7}}$ para eliminar la raíz cuadrada en el denominador:

4 \sqrt{3} \sqrt{7} \times \frac{\sqrt{7}}{\sqrt{7}}

${frac{4{sqrt{3}}}{{sqrt{7}}}}times {frac{{sqrt{7}}}{{sqrt{7}}}}$

= 4 \sqrt{3} \times \sqrt{7} \sqrt{7} \times \sqrt{7}

$={frac{4{sqrt{3}}times {sqrt{7}}}{{sqrt{7}}times {sqrt{7}}}}$

= 4 \sqrt{21} \sqrt{49}

$={frac{4{sqrt{21}}}{{sqrt{49}}}}$

= 4 \sqrt{21} 7

$={frac{4{sqrt{21}}}{7}}$

Método 4 de 4: Dividir por un binomio con raíz cuadrada

Imagen titulada Dividir raíces cuadradas Paso 14

1. Determina si tienes un binomio en el denominador. El denominador es el número en el problema que estás dividiendo por. Un binomio es un polinomio con dos términos. Este método solo se aplica a la división de raíces cuadradas que involucran un binomio.

Por ejemplo, si usted $1 5 + \sqrt{2}$ ${frac{1}{5+{sqrt{2}}}}$ Si quieres calcular, tienes un binomio en el denominador, porque $5 + \sqrt{2}$ $5+{sqrt{2}}$ es un polinomio con dos términos.

Imagen titulada Dividir raíces cuadradas Paso 15

2. Determinar la conjunción del binomio. Los pares conjugados son binomios con los mismos términos pero operadores opuestos. Usando un par de subjuntivos puedes eliminar la raíz cuadrada del denominador.

Por ejemplo,

5 + \sqrt{2}

$5+{sqrt{2}}$ y

5 - \sqrt{2}

$5-{raíz cuadrada{2}}$ son pares conjuntivos, porque tienen los mismos términos, pero operadores opuestos.

Imagen titulada Dividir raíces cuadradas Paso 16

3. Multiplicar el numerador y el denominador por la conjunción del denominador. Esto te permite eliminar la raíz cuadrada, porque el producto de un par conjugado es la diferencia del cuadrado de cada término en el binomio. Es decir,

(a - B) (a + B) = a 2 - B^{2}

$(a-b)(a+b)=a^{{2}}-b^{{2}}$ .

Por ejemplo:

1 5 + \sqrt{2}

${frac{1}{5+{sqrt{2}}}}$

= 1 (5 - \sqrt{2}) (5 + \sqrt{2}) (5 - \sqrt{2})

$={frac{1(5-{sqrt{2}})}{(5+{sqrt{2}})(5-{sqrt{2}})}}$

= 5 - \sqrt{2} (5 2 - (\sqrt{2})^{2}

$={frac{5-{sqrt{2}}}{(5^{{2}}-({sqrt{2}})^{{2}}}}$

= 5 + \sqrt{2} 25 - 2

$={frac{5+{sqrt{2}}}{25-2}}$

= 5 + \sqrt{2} 23

$={frac{5+{sqrt{2}}}{23}}$
por lo tanto,

1 5 + \sqrt{2} = 5 + \sqrt{2} 23

${frac{1}{5+{sqrt{2}}}}={frac{5+{sqrt{2}}}{23}}$ .

Consejos

Muchas calculadoras tienen funciones especiales para fracciones. Ingrese el coeficiente del numerador, presione el botón de fracciones, luego ingrese el coeficiente del denominador. Cuando presiona el signo igual después, la calculadora debería haber reescrito los coeficientes en los términos más pequeños.
A diferencia de la suma y resta de raíces, en una fracción no es necesario simplificar primero las raíces para quitar los cuadrados. De hecho, a menudo es mejor no hacer esto.
Si trabajas con raíces cuadradas, las fracciones impropias son más fáciles de resolver que los números mixtos.

Advertencias

Nunca pongas un decimal en una fracción. De lo contrario, sería una fracción dentro de una fracción.
Nunca anteponga un número decimal o mixto a una raíz, conviértalo en una fracción y simplifique la expresión completa.
Nunca deje una raíz cuadrada en el denominador de una fracción, pero simplifique la fracción.
Si el denominador contiene alguna forma de suma o resta, use el método del par conjugado para eliminar el radical del denominador.