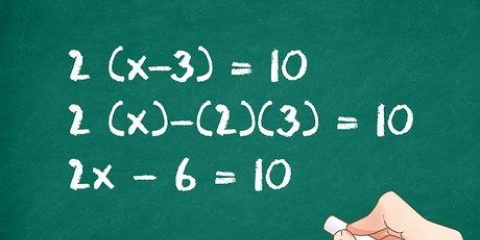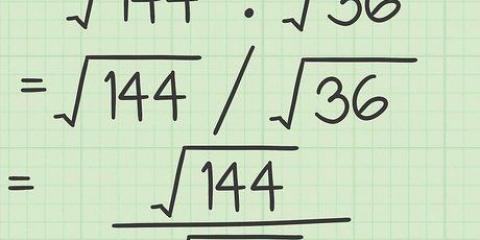Está claro aquí por qué  , porque
, porque  está en el denominador y no se puede dividir por cero.
está en el denominador y no se puede dividir por cero. Si lo necesita, puede extender el lado izquierdo para asegurarse de que el cuadrado funcione. 

Ahora podemos deshacernos de los signos de valor absoluto, por  colocar a la derecha. Podemos hacer esto porque el valor absoluto no distingue entre números positivos y negativos, por lo que ambos son válidos. Este detalle es el por qué la ecuación cuadrática permite obtener dos raíces como resultado.
colocar a la derecha. Podemos hacer esto porque el valor absoluto no distingue entre números positivos y negativos, por lo que ambos son válidos. Este detalle es el por qué la ecuación cuadrática permite obtener dos raíces como resultado. 
Simplifiquemos un poco más esta expresión. Como la raíz cuadrada de un cociente es el cociente de las raíces cuadradas, podemos escribir el lado derecho como  Entonces podemos sacar la raíz cuadrada del denominador.
Entonces podemos sacar la raíz cuadrada del denominador. 


Aprende la división de cuadrados
Una de las habilidades más importantes para los estudiantes de matemáticas es la fórmula abc, o 


Pasos
1. Comience con la forma estándar de una ecuación cuadrática general. Aunque cualquier comparación con un término como  in, es cuadrático, la forma estándar pone todo a cero. Recuérdalo
in, es cuadrático, la forma estándar pone todo a cero. Recuérdalo  son coeficientes que pueden ser cualquier número entero, por lo que ahora no puede completar los números de las variables; queremos trabajar con la forma general.
son coeficientes que pueden ser cualquier número entero, por lo que ahora no puede completar los números de las variables; queremos trabajar con la forma general.
 in, es cuadrático, la forma estándar pone todo a cero. Recuérdalo
in, es cuadrático, la forma estándar pone todo a cero. Recuérdalo  son coeficientes que pueden ser cualquier número entero, por lo que ahora no puede completar los números de las variables; queremos trabajar con la forma general.
son coeficientes que pueden ser cualquier número entero, por lo que ahora no puede completar los números de las variables; queremos trabajar con la forma general. - La única condición es que
, de lo contrario, la ecuación se simplifica a una ecuación lineal. Vea si puede encontrar soluciones generales para casos especiales donde
y
.
2. jalar C  fuera de ambos lados. Nuestro objetivo es aislar
fuera de ambos lados. Nuestro objetivo es aislar  . Comenzamos moviendo uno de los coeficientes al otro lado para que el lado izquierdo consista solo de términos con
. Comenzamos moviendo uno de los coeficientes al otro lado para que el lado izquierdo consista solo de términos con  .
.
 fuera de ambos lados. Nuestro objetivo es aislar
fuera de ambos lados. Nuestro objetivo es aislar  . Comenzamos moviendo uno de los coeficientes al otro lado para que el lado izquierdo consista solo de términos con
. Comenzamos moviendo uno de los coeficientes al otro lado para que el lado izquierdo consista solo de términos con  .
.
3. Dividir ambos lados a  . Tenga en cuenta que podríamos haberlos intercambiado en el paso anterior y obtener la misma respuesta. Recuerda que dividir un polinomio por algo implica dividir cada uno de sus términos individuales. Esto hace que sea más fácil dividir el cuadrado.
. Tenga en cuenta que podríamos haberlos intercambiado en el paso anterior y obtener la misma respuesta. Recuerda que dividir un polinomio por algo implica dividir cada uno de sus términos individuales. Esto hace que sea más fácil dividir el cuadrado.
 . Tenga en cuenta que podríamos haberlos intercambiado en el paso anterior y obtener la misma respuesta. Recuerda que dividir un polinomio por algo implica dividir cada uno de sus términos individuales. Esto hace que sea más fácil dividir el cuadrado.
. Tenga en cuenta que podríamos haberlos intercambiado en el paso anterior y obtener la misma respuesta. Recuerda que dividir un polinomio por algo implica dividir cada uno de sus términos individuales. Esto hace que sea más fácil dividir el cuadrado.
4.dividir el cuadrado. Recuerda que el objetivo es crear una expresión  reescribir como
reescribir como  por lo cual
por lo cual  es un coeficiente. Es posible que esto no te quede claro de inmediato. Para que quede más claro, reescribe
es un coeficiente. Es posible que esto no te quede claro de inmediato. Para que quede más claro, reescribe  Si
Si  multiplicando el término por
multiplicando el término por  Podemos hacer esto porque multiplicar por 1 no cambia nada. Ahora podemos ver claramente en nuestro caso que
Podemos hacer esto porque multiplicar por 1 no cambia nada. Ahora podemos ver claramente en nuestro caso que  , entonces solo falta el termino
, entonces solo falta el termino  . Por lo tanto, para dividir el cuadrado, lo sumamos en ambos lados, a saber,
. Por lo tanto, para dividir el cuadrado, lo sumamos en ambos lados, a saber,  Y luego, por supuesto, podemos factorizar.
Y luego, por supuesto, podemos factorizar.
 reescribir como
reescribir como  por lo cual
por lo cual  es un coeficiente. Es posible que esto no te quede claro de inmediato. Para que quede más claro, reescribe
es un coeficiente. Es posible que esto no te quede claro de inmediato. Para que quede más claro, reescribe  Si
Si  multiplicando el término por
multiplicando el término por  Podemos hacer esto porque multiplicar por 1 no cambia nada. Ahora podemos ver claramente en nuestro caso que
Podemos hacer esto porque multiplicar por 1 no cambia nada. Ahora podemos ver claramente en nuestro caso que  , entonces solo falta el termino
, entonces solo falta el termino  . Por lo tanto, para dividir el cuadrado, lo sumamos en ambos lados, a saber,
. Por lo tanto, para dividir el cuadrado, lo sumamos en ambos lados, a saber,  Y luego, por supuesto, podemos factorizar.
Y luego, por supuesto, podemos factorizar.
 , porque
, porque  está en el denominador y no se puede dividir por cero.
está en el denominador y no se puede dividir por cero.5. Escribe el lado derecho bajo un denominador común. Queremos que ambos denominadores sean  son, así que multiplica el término
son, así que multiplica el término  de
de  .
.
 son, así que multiplica el término
son, así que multiplica el término  de
de  .
.
6. Calcular la raíz cuadrada de ambos lados. Sin embargo, es esencial que comprenda que al hacer esto esencialmente está dando dos pasos. Cuando sacas la raíz cuadrada de  , entonces obtienes
, entonces obtienes  no. Básicamente obtienes el valor absoluto,
no. Básicamente obtienes el valor absoluto,  . Este valor absoluto es esencial para obtener ambas raíces: simplemente colocar raíces cuadradas sobre ambos lados solo producirá una de las raíces.
. Este valor absoluto es esencial para obtener ambas raíces: simplemente colocar raíces cuadradas sobre ambos lados solo producirá una de las raíces.
 , entonces obtienes
, entonces obtienes  no. Básicamente obtienes el valor absoluto,
no. Básicamente obtienes el valor absoluto,  . Este valor absoluto es esencial para obtener ambas raíces: simplemente colocar raíces cuadradas sobre ambos lados solo producirá una de las raíces.
. Este valor absoluto es esencial para obtener ambas raíces: simplemente colocar raíces cuadradas sobre ambos lados solo producirá una de las raíces.
 colocar a la derecha. Podemos hacer esto porque el valor absoluto no distingue entre números positivos y negativos, por lo que ambos son válidos. Este detalle es el por qué la ecuación cuadrática permite obtener dos raíces como resultado.
colocar a la derecha. Podemos hacer esto porque el valor absoluto no distingue entre números positivos y negativos, por lo que ambos son válidos. Este detalle es el por qué la ecuación cuadrática permite obtener dos raíces como resultado.
 Entonces podemos sacar la raíz cuadrada del denominador.
Entonces podemos sacar la raíz cuadrada del denominador.
7. aislar X  restando
restando B 2 a  a ambos lados.
a ambos lados.
 restando
restando  a ambos lados.
a ambos lados.
8. Escribe el lado derecho bajo un denominador común. Esto no es como la fórmula abc, la fórmula para resolver una ecuación cuadrática en forma estándar. Esto funciona para cualquier  y da
y da  como resultado, que puede ser un número real o complejo. Para verificar que este proceso funciona, simplemente siga los pasos de este artículo en orden inverso para volver al formulario predeterminado.
como resultado, que puede ser un número real o complejo. Para verificar que este proceso funciona, simplemente siga los pasos de este artículo en orden inverso para volver al formulario predeterminado.
 y da
y da  como resultado, que puede ser un número real o complejo. Para verificar que este proceso funciona, simplemente siga los pasos de este artículo en orden inverso para volver al formulario predeterminado.
como resultado, que puede ser un número real o complejo. Para verificar que este proceso funciona, simplemente siga los pasos de este artículo en orden inverso para volver al formulario predeterminado.
Consejos
- Es interesante notar que la fórmula abc también se aplica a coeficientes complejos, aunque tienes que simplificar un poco más para obtener la respuesta final, y las raíces no son pares conjugados. Sin embargo, los problemas con expresiones cuadráticas casi siempre se dan con coeficientes reales.
Artículos sobre el tema. "Aprende la división de cuadrados"
Оцените, пожалуйста статью
Similar
Popular