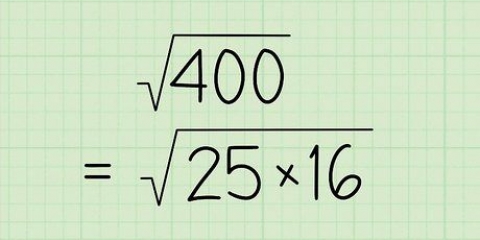3(x - 2/3) =
3(x - 2/3)(x -2/3) = 3[(x -2/3x -2/3x + 4/9)] 3(x - 4/3x + 4/9) 
-4/3 + 15/3 = 11/3.










Cuadrado partido
Contenido
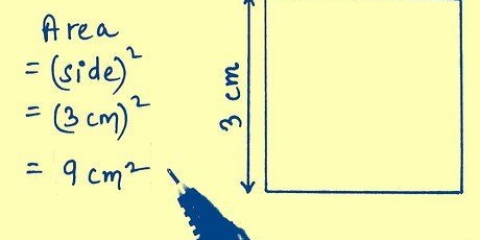
Elevar al cuadrado es una técnica útil para reescribir una ecuación cuadrática, lo que facilita su supervisión y resolución. Puedes reescribir un cuadrado reorganizándolo en partes más manejables.
Pasos
Método 1 de 2: Primera parte: Reescribir una ecuación estándar

1. escribe la ecuacion. Supongamos que desea resolver la siguiente ecuación: 3x - 4x + 5.

2. Eliminar el coeficiente de la ecuación. Coloque los 3 corchetes exteriores y divida cada término excepto la constante por 3. 3x dividido por 3 es x y 4x dividido por 3 es 4/3x. Así que la nueva ecuación se ve así: 3(x - 4/3x) + 5. El 5 está fuera de los corchetes porque no lo dividiste por 3.

3. Divide el segundo término por 2 y eleva al cuadrado. El segundo término, también llamado B-término en la ecuación, es 4/3. Reducir a la mitad el segundo término. 4/3 ÷ 2, o 4/3 x 1/2, es igual a 2/3. Eleve al cuadrado este término multiplicando el numerador y el denominador por sí mismos. (2/3) = 4/9. Escribe este término.

4. Adición y sustracción. lo tienes"adicional" término necesario para convertir los tres primeros términos de la ecuación en un cuadrado. Pero recuerda que sumaste este término restándolo también de la ecuación. Por supuesto, no hace mucha diferencia simplemente combinar los términos de nuevo, entonces estarás de vuelta donde empezaste. La nueva ecuación ahora debería verse así: 3( x - 4/3 x + 4/9 - 4/9) + 5.

5. Obtén el término que restaste fuera de los paréntesis. Debido a que ya está trabajando con el 3 fuera de los corchetes, no es posible simplemente poner -4/9 fuera de los corchetes. primero hay que multiplicarlo por 3. -4/9 x 3 = -12/9 o -4/3. Si está tratando con una ecuación que solo contiene un coeficiente 1 de x, puede omitir este paso.

6. Convierte los términos entre paréntesis en un cuadrado. Tu ecuación ahora se ve así: 3(x -4/3x +4/9). Trabajaste de adelante hacia atrás para obtener 4/9, que en realidad es otra forma de encontrar el factor que completa el cuadrado. Entonces puedes reescribir estos términos como: 3(x - 2/3). Puede verificar esto multiplicando donde verá que obtiene la misma ecuación original que la respuesta nuevamente.


7. fusionar las constantes. Ahora tienes dos constantes, 3(x - 2/3) - 4/3 + 5. Todo lo que tienes que hacer ahora es sumar -4/3 a 5 y esto da 11/3 como respuesta. Haces esto dándoles el mismo denominador: -4/3 y 15/3, luego sumando ambos numeradores para obtener 11, manteniendo el denominador igual a 3.


8. Escribe la ecuación en otra forma. ahora ya terminaste. La ecuación final es 3(x - 2/3) + 11/3. Puedes eliminar el 3 dividiendo la ecuación por 3, dejándote con la siguiente ecuación:(x - 2/3) + 11/9.Ahora ha escrito con éxito la ecuación en otra forma: a( x - h ) + k, por lo cual k la constante es.
Método 2 de 2: Segunda parte: Resolver una ecuación cuadrática

1. Tenga en cuenta la tarea. Supongamos que desea resolver la siguiente ecuación: 3x + 4x + 5 = 6

2. Sume las constantes y colóquelas a la izquierda del signo igual. Los términos constantes son aquellos términos sin una variable. En este caso tienes 5 a la izquierda y 6 a la derecha. Quieres mover 6 a la izquierda, así que resta 6 de ambos lados de la ecuación. Esto deja 0 a la derecha (6-6) y -1 a la izquierda (5-6). La ecuación ahora se ve así: 3x + 4x - 1 = 0.

3. Saca el coeficiente del cuadrado fuera de los corchetes. En este caso, 3 es el coeficiente de x. Para excluir 3 de los paréntesis, elimine el 3, coloque el término restante entre paréntesis y divida cada término por 3. Entonces, 3x ÷ 3 = x, 4x ÷ 3 = 4/3x, y 1 ÷ 3 = 1/3. La ecuación ahora se ve así: 3(x + 4/3x - 1/3) = 0.

4. Divide por la constante que acabas de poner entre paréntesis. Con esto por fin te deshaces de esos molestos 3 fuera de los corchetes. Al dividir cada término por 3, se puede eliminar sin cambiar la ecuación. Ahora tienes: x + 4/3x - 1/3 = 0

5. Divide el segundo término por 2 y eleva al cuadrado. Ahora toma el segundo término, 4/3, de B término, y dividir por 2. 4/3 2 o 4/3 x 1/2, es 4/6 o 2/3. y 2/3 al cuadrado es 4/9. Cuando haya terminado con esto, debe escribirlo a la izquierda y a la derecha de la ecuación porque básicamente acaba de agregar un nuevo término. Tienes que hacer esto en ambos lados de la ecuación. La ecuación ahora se ve así: x + 4/3 x + 2/3 - 1/3 = 2/3

6. Mueva la constante original al lado derecho de la ecuación y súmela al término que ya está allí. Mueva la constante, -1/3, a la derecha para que sea 1/3. Agregue esto al otro término, 4/9 o 2/3. Encuentra el mínimo común múltiplo para poder sumar 1/3 y 4/9. Esto es así: 1/3 x 3/3 = 3/9. Ahora suma 3/9 a 4/9 para que tengas 7/9 en el lado derecho de la ecuación. Esto da: x + 4/3 x + 2/3 = 4/9 + 1/3 y luego x + 4/3 x + 2/3 = 7/9.

7. Escribe el lado izquierdo de la ecuación como un cuadrado. Como ya usaste una fórmula para encontrar el término que falta, la parte más difícil ya está hecha. Todo lo que tienes que hacer es poner la x y la mitad del segundo coeficiente entre paréntesis y elevarlo al cuadrado, así :(x + 2/3). Tenga en cuenta que factorizar el cuadrado produce 3 términos: x + 4/3 x + 4/9. La ecuación ahora se ve así: (x + 2/3) = 7/9.

8. Saca la raíz cuadrada de ambos lados de la ecuación. En el lado izquierdo de la ecuación, la raíz cuadrada de (x + 2/3) es igual a x + 2/3. El lado derecho da +/- (√7)/3. La raíz cuadrada del denominador 9 es 3 y la raíz cuadrada de 7 es √7. No olvides escribir el +/- porque la raíz cuadrada de un número puede ser positiva o negativa.

9. Deja la variable a un lado. Para aislar la variable x del resto, mueva la constante 2/3 al lado derecho de la ecuación. Ahora tiene dos respuestas posibles para x:+/- (√7)/3 - 2/3. estas son tus dos respuestas. Puedes dejarlo así o elaborar la raíz cuadrada, si te piden una respuesta sin radical.
Consejos
- Asegúrate de poner el +/- en los lugares correctos, de lo contrario solo obtendrás una respuesta.
- Incluso si conoces la fórmula de la raíz cuadrada, no está de más practicar la división de cuadrados o resolver ecuaciones cuadráticas de vez en cuando. Así sabrás con certeza que sabes cómo hacerlo cuando sea necesario.
Artículos sobre el tema. "Cuadrado partido"
Оцените, пожалуйста статью
Similar
Popular