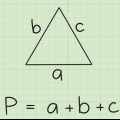Cómo calcular la circunferencia de un cuadrado

Contenido

Pasos

El perímetro de una figura bidimensional es la distancia total alrededor de la figura, o la suma de las longitudes de los lados. La definición de un cuadrado es una figura con cuatro lados iguales y cuatro ángulos rectos (90°) entre esos lados. Como todos los lados tienen la misma longitud, es muy fácil determinar el perímetro de un cuadrado! Este artículo cubre primero cómo calcular el perímetro de un cuadrado si conoce la longitud de uno de sus lados. Luego te mostraremos cómo calcular el perímetro si solo conoces el área, y en la última sección te enseñaremos cómo calcular el perímetro de un cuadrado inscrito en un círculo cuya longitud del radio se conoce.

Pasos

Método 1 de 3: encontrar el perímetro de un cuadrado si conoces la longitud de un lado

Imagen titulada Calcular el perímetro de un cuadrado Paso 1

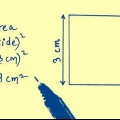
1. Piensa en la fórmula para el perímetro de un cuadrado. Para un cuadrado donde encontramos la longitud del lado s el perímetro es simplemente cuatro veces la longitud de ese lado: Circunferencia = 4s (nota: en las imágenes se usa la letra P para el contorno, del inglés `Perimeter`).

Imagen titulada Calcular el perímetro de un cuadrado Paso 2

2. Encuentra la longitud de un lado y multiplícalo por 4 para encontrar el perímetro. Dependiendo de la tarea, es posible que deba medir con una regla o mirar otra información para determinar la longitud de un lado. Estos son algunos ejemplos de cálculos de circunferencia:

Si el cuadrado tiene un lado de longitud 4:Circunferencia = 4 * 4, en otras palabras dieciséis.

Si el cuadrado tiene un lado de longitud 6: Circunferencia = 4 * 6, en otras palabras 24.

Método 2 de 3: Determinar el perímetro de un cuadrado si conoces su área

Imagen titulada Calcular el perímetro de un cuadrado Paso 3

1. Conoce la fórmula del área de un cuadrado. El área de cualquier rectángulo (recuerda que los cuadrados son rectángulos especiales) se puede definir como base por altura.Dado que la base y la altura son iguales en el caso de un cuadrado, el área de un cuadrado de lado s: sexo. En otras palabras: área = s.

Imagen titulada Calcular el perímetro de un cuadrado Paso 4

2. Saca la raiz cuadrada del area. La raíz cuadrada del área te da la longitud de uno de los lados del cuadrado. Para la mayoría de los números necesitas una calculadora para calcular la raíz cuadrada. Escriba el número primero, luego presione la tecla raíz cuadrada (√).

Si el área del cuadrado es 20, entonces la longitud del lado es s: =√20 o 4.472

Si el área del cuadrado es 25, entonces la longitud del lado es s = √25 o 5.

Imagen titulada Calcular el perímetro de un cuadrado Paso 5

3. Multiplica la longitud del lado por 4 para encontrar la circunferencia. Usa el valor de la longitud del lado que acabas de encontrar en la fórmula Circunferencia = 4s. El resultado es el perímetro de tu cuadrado!

Para un cuadrado con un área de 20 y una longitud de lado de 4,473, el perímetro es: Circunferencia = 4 * 4.472 o 17,888.

Para un cuadrado con un área de 25 y una longitud de lado de 5, el perímetro es: Circunferencia = 4 * 5 o 20.

Método 3 de 3: calcular el perímetro de un cuadrado inscrito en un círculo si conoces el radio

Imagen titulada Calcular el perímetro de un cuadrado Paso 6

1. Comprender qué es un cuadrado inscrito. Un cuadrado inscrito en un círculo es un cuadrado dibujado en un círculo con todas las esquinas del cuadrado tocando el círculo.

Imagen titulada Calcula el perímetro de un cuadrado Paso 7

2. Comprender la relación entre el radio del círculo y la longitud de los lados del cuadrado. La distancia del centro de un cuadrado inscrito a cualquier esquina es igual al radio del círculo. A la longitud lateral s para encontrar, primero debemos imaginar que cortamos el cuadrado por la mitad en diagonal, de modo que se formen dos triángulos equiláteros. Estos triángulos tienen lados iguales a y B y una hipotenusa C, que sabemos que es igual al doble del radio del círculo, es decir 2r.

Imagen titulada Calcular el perímetro de un cuadrado Paso 8

3. Usa el teorema de Pitágoras para encontrar la longitud del lado del cuadrado. El teorema de Pitágoras es el siguiente: en un triángulo rectángulo, la suma de los cuadrados de las longitudes de los lados rectangulares (a,b) es igual al cuadrado de la longitud de la hipotenusa (c), a + b = c. porque los lados a y B son iguales (todavía estamos tratando con un cuadrado!) y sabemos que c=2r ahora podemos escribir la ecuación y simplificarla para encontrar la longitud de un lado:

a + a = (2r), ahora podemos simplificar:

2a = 4(r), ahora divide ambos lados por 2:

(a) = 2(r), Ahora saca la raíz cuadrada de cada lado:

a = √(2)r.Nuestra longitud de un lado s del cuadrado inscrito = √(2)r.

Imagen titulada Calcula el perímetro de un cuadrado Paso 9

4. Multiplica la longitud de un lado del cuadrado por cuatro para encontrar el perímetro. En este caso, el perímetro del cuadrado es: Circunferencia = 4√(2)r. Por lo tanto, la circunferencia de un cuadrado inscrito en un círculo es siempre igual a 4√(2)r, o alrededor de 5.657r

Imagen titulada Calcula el perímetro de un cuadrado Paso 10

5. Resolver una pregunta de ejemplo. Tomamos un cuadrado inscrito en un círculo con un radio de 10. Eso significa que la diagonal del cuadrado = 2(10) o 20. El teorema de Pitágoras nos enseña que: 2(a) = 20, Entonces 2a = 400. Ahora dividimos ambos lados por dos, vemos que un = 200. Saca la raíz cuadrada de cada lado y vemos que = 14,142. Multiplique esto por 4 para encontrar el perímetro de su cuadrado: Circunferencia = 56,57.

Nota: también podrías haberlo hecho de esta manera: multiplica el radio (10) por el número 5,567. 10*5.567 = 56.57, pero como eso puede ser difícil de recordar, es mejor que sigas todo el proceso.