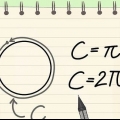Calcular circunferencia por área: 10 pasos (con fotos)

Contenido

Pasos
- Método 1 de 2: usar la ecuación del perímetro
- Método 2 de 2: solucionar el problema a la inversa

La fórmula para calcular la circunferencia (C) de un círculo, C = πD o C = 2πR, es simple si conoce el diámetro (D) o el radio (R) del círculo. Pero que haces si solo sabes el area del circulo? Como muchas cosas en matemáticas, hay múltiples soluciones para este problema. La fórmula C = 2√πA está diseñada para encontrar la circunferencia de un círculo usando el área (A). También puede invertir la ecuación A = πR para encontrar R, luego ingrese R en la ecuación del perímetro. Ambas ecuaciones dan el mismo resultado.

Pasos

Método 1 de 2: usar la ecuación del perímetro

Imagen titulada Encuentra la circunferencia de un círculo usando su área Paso 1

1. Usa la fórmula C=2√πA para resolver el problema. Esta fórmula calcula la circunferencia de un círculo si solo conoces su área. C representa el perímetro y A el área. Escribe esta fórmula para empezar a resolver el problema.

El símbolo π, que significa pi, es un decimal periódico con (por ahora) miles de dígitos después del punto decimal. Para simplificar, use 3.14 como el valor de pi.
Como tienes que convertir pi a su forma numérica de todos modos, usa 3.14 en la ecuación desde el principio. Escríbelo como C = 2√3.14 x A.

Imagen titulada Encuentra la circunferencia de un círculo usando su área Paso 2

2. Incluir el área como A en la ecuación. Como ya sabes el área del círculo, ese es el valor de A. Luego procede a resolver el problema usando el orden de las operaciones.

Digamos que el area del circulo es de 500 cm. Luego resuelves la ecuación de la siguiente manera: 2√3.14 x 500.

Imagen titulada Encuentra la circunferencia de un círculo usando su área Paso 3

3. Multiplica pi por el area del circulo. En el orden de las operaciones, las operaciones dentro del símbolo de la raíz cuadrada van primero. Multiplica pi por el área del círculo que enchufaste. Luego reemplaza ese resultado en la ecuación.

Si el cálculo es igual a 2√3,14 x 500, primero calcula 3,14 x 500 = 1570. Luego calcula 2√1,570.

Imagen titulada Encuentra la circunferencia de un círculo usando su área Paso 4

4. Especialraíz cuadrada de la suma. Hay varias formas de calcular la raíz cuadrada. Si está usando una calculadora, presione la función √ y escriba el número. También puedes resolver el problema a mano usando factores primos.

La raíz cuadrada de 1570 es 39.6.

Imagen titulada Encuentra la circunferencia de un círculo usando su área Paso 5

5. Multiplica la raíz cuadrada por 2 para encontrar el perímetro. Finalmente, completas el cálculo multiplicando el resultado por 2. Esto devuelve un número final, la circunferencia.

Calcula 39,6 x 2 = 79,2. Esto significa que la circunferencia es de 79,2 cm, lo que resuelve la fórmula.

Método 2 de 2: solucionar el problema a la inversa

Imagen titulada Encuentra la circunferencia de un círculo usando su área Paso 6

1. Utilice la fórmula A = πR en. esta es la formula del area de un circulo. A representa el área y R el radio. Normalmente lo usaría si supiera el radio, pero también puede completar el área para resolver la ecuación.

Nuevamente, use 3.14 como valor redondeado para pi.

Imagen titulada Encuentra la circunferencia de un círculo usando su área Paso 7

2. Ingrese el área como valor para A. Usa el área del círculo en la ecuación. Coloque esto a la izquierda de la ecuación como el valor para A.

Supongamos que el área del círculo es de 200 cm. La ecuación entonces se convierte en 200 = 3.14 x R.

Imagen titulada Encuentra la circunferencia de un círculo usando su área Paso 8

3. Divide ambos lados de la ecuación por 3.14. Para resolver este tipo de ecuación, debes eliminar gradualmente los pasos de la derecha haciendo las operaciones opuestas. Como sabes el valor de pi, divides cada lado por ese valor. Esto elimina pi a la derecha y le da un nuevo valor numérico a la izquierda.

Si divides 200 entre 3,14, el resultado es 63,7. Entonces la nueva ecuación es 63.7 = R.

Imagen titulada Encuentra la circunferencia de un círculo usando su área Paso 9

4. Especialraíz cuadrada del resultado para obtener el radio del círculo. Luego se elimina el exponente del lado derecho de la ecuación. Lo contrario de `exponenciación` es encontrar la raíz cuadrada del número. Encuentra la raíz cuadrada de cada lado de la ecuación. Esto elimina el exponente a la derecha y pone el radio a la izquierda.

La raíz cuadrada de 63.7 es 7.9. La ecuación entonces se convierte en 7.9 = R, lo que significa que el radio del círculo es 7.9. Esto le dará toda la información que necesita para encontrar el perímetro.

Imagen titulada Encuentra la circunferencia de un círculo usando su área Paso 10

5.determinar la circunferencia del círculo usando el radio. Hay dos fórmulas para encontrar el perímetro (C). El primero es C = πD, donde D es el diámetro. Multiplica el radio por 2 para encontrar el diámetro. El segundo es C = 2πR. Multiplica 3,14 por 2 y luego multiplica el resultado por el radio. Ambas fórmulas te darán el mismo resultado.

Usa la primera opción, 7.9 x 2 = 15.8, el diámetro del círculo. Este diámetro multiplicado por 3,14 es 49,6.

Para la segunda opción, el cálculo se convierte en 2 x 3,14 x 7,9. Primero calculas 2 x 3.14 = 6.28, y eso multiplicado por 7.9 es 49.6. Observe cómo ambos métodos le dan la misma respuesta.