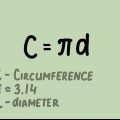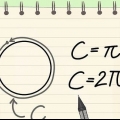Incluso el botón π en una calculadora no usa el valor exacto de π, aunque es lo suficientemente preciso. 
C es solo una forma más corta de escribir `circunferencia`. 
Es posible que haya escrito el lado izquierdo como π2r, que también es correcto. A la gente le gusta poner los números antes de los símbolos para que la ecuación sea más fácil de leer, pero esto no cambia el resultado de la ecuación. En una ecuación matemática, siempre puedes multiplicar los lados izquierdo y derecho por la misma cantidad y aun así obtener una ecuación correcta. 
Por ejemplo, si el radio mide dos unidades, entonces 2πr = 2 x (3,14) x (2 unidades) = 12,56 unidades = la circunferencia. En el mismo ejemplo, pero usando el botón π de una calculadora para mayor precisión, obtienes 2 x π x 2 unidades = 12,56637... unidades, pero a menos que su maestro le indique lo contrario, puede redondear el número a 12.57 unidades. 

Usamos D`, no2r, porque tu problema de matemáticas te dice qué D medio. Sin embargo, es importante comprender este paso para que no se confunda si su maestro o libro de matemáticas 2r utilizado donde usted tiene un D Esperaría. 
Incluso el botón π en una calculadora no usa el valor exacto de π, aunque es muy preciso. 

π x re = (C / re) x re πd = C 
Por ejemplo, si el diámetro es seis, obtienes (3,14) x (6) = 18,84. En el mismo ejemplo, pero usando el botón π de una calculadora para mayor precisión, obtienes π x 6 = 18.84956... pero a menos que se indique lo contrario, puede redondear el número a 18,85. 


A = r A / π = πr / π = r √(A/π) = √(r) = r r = √(A/π) 
C = 2πr C = 2π(√(A/π)) 
La respuesta para este ejemplo es 13.72937... pero a menos que se indique lo contrario, puede redondear la respuesta a 13.73. 


Asegúrate de envolver la cuerda alrededor de él más de una vez. Debes terminar con un solo lazo para que no haya ninguna parte del círculo donde la cuerda esté doblemente enrollada. 

Encontrar la circunferencia de un círculo
Contenido
La circunferencia de un círculo es la distancia alrededor de su borde. Si un círculo tiene una circunferencia de 2 millas, entonces debes caminar alrededor del círculo 2 millas antes de regresar al punto de partida. Sin embargo, si estás trabajando en un problema geométrico, no tienes que levantarte de tu silla. Lea el problema cuidadosamente para averiguar si se da el `radio` (r), el `diámetro` (d) o el `área` (A) del círculo, y luego encuentre la parte de este artículo que pretende ayudarlo. con la tarea. También hay instrucciones para encontrar el perímetro de un objeto circular existente que desea medir.
Pasos
Método 1 de 4: Determinar el perímetro usando el radio

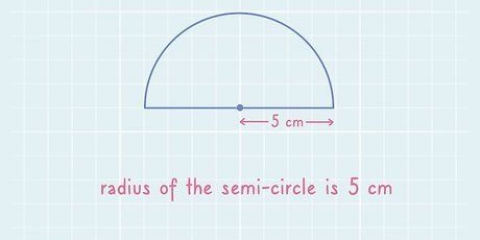
1. Dibuja un `rayo` en el círculo. Dibuja una línea desde el centro del círculo hasta cualquier posición en el borde del círculo. Esta línea es el `radio` del círculo, a menudo escrito como `r` en ecuaciones y fórmulas matemáticas.
- `Observación: si el radio no se proporciona en el problema matemático, es posible que estas no sean las instrucciones correctas. A ver si los del diámetro o la superficie son más útiles para el trabajo.

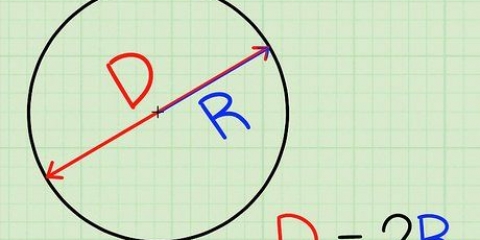
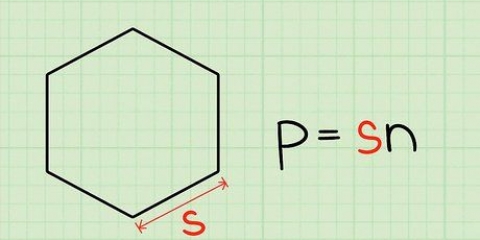
2. Dibujar un `diámetro` sobre el círculo. Extienda la línea que acaba de dibujar para que alcance el borde del círculo en el otro lado. Acabas de dibujar un segundo rayo. Los dos radios sumados tienen una longitud de `2 x el radio`, escrito como 2r. La longitud de esta línea es el `diámetro` del círculo, a menudo escrito como D.

3. Entender π (`pi`). El símbolo π, también escrito como Pi no es un número mágico que se usa en este tipo de problemas matemáticos. En realidad, el número π se `descubrió` originalmente midiendo círculos: si mides la circunferencia de cualquier círculo (por ejemplo, con una cinta métrica) y luego la divides por el diámetro, siempre obtienes el mismo número. Este número es inusual porque no se puede escribir como una fracción simple o decimal. En su lugar, podemos redondearlo a un número como 3,14, que es "suficientemente bueno".

4. Escribe la definición de π como un problema de álgebra. Como se explicó anteriormente, π solo significa `el número que obtienes cuando divides la circunferencia por el diámetro`. En forma de fórmula matemática esto es: π = C / re. Como sabemos que el diámetro es igual a 2 x el radio, también podemos escribir esto como π = C / 2r.

5. Cambia este problema para que resuelvas este problema para el perímetro C. Queremos saber cuál es el perímetro (C en este problema de matemáticas). Si multiplicas ambos lados por 2r usted obtiene π x 2r = (C / 2r) x 2r, y eso es lo mismo que 2πr = C.

6. Sustituye los números para resolver C. Ahora sabemos que 2πr = C. Regrese al problema matemático original para ver qué r (el radio) es. Luego reemplace π con 3.14, o use el botón π en su calculadora para obtener una respuesta más precisa. Calcula 2πr con estos números. La respuesta que obtienes es la circunferencia.
Método 2 de 4: Determinar la circunferencia usando el diámetro

1. Comprender qué es un `diámetro`. Coloca tu lápiz en el borde del círculo. Dibuja una línea a través del centro del círculo y el borde del otro lado. Esta línea (de borde a borde y a través del centro) es el `diámetro` del círculo, a menudo escrito como D en problemas de matemáticas.
- La línea pasa por el centro exacto del círculo, no por cualquier parte del círculo.
- Observación: Si la declaración no indica cuánto mide el diámetro, use otro método.

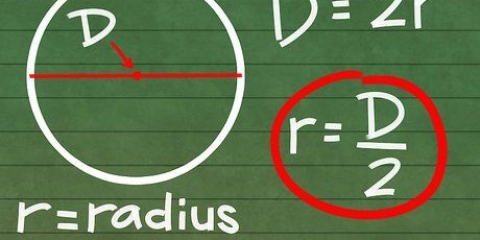
2. Aprende lo que significa d = 2r. El `radio` del círculo, también escrito como r, es la distancia del centro al borde del circulo. Como el diámetro pasa por el círculo de borde a borde, pasando por el centro, el diámetro es igual a dos radios. Una manera fácil de escribir esto es d = 2r. Esto significa que usted D siempre se puede reemplazar con 2r en un problema de matemáticas y viceversa.

3. Entender π (`pi`). El símbolo π, también escrito como Pi no es un número mágico que se usa en este tipo de problemas matemáticos. En realidad, el número π se `descubrió` originalmente midiendo círculos: si mides la circunferencia de cualquier círculo (por ejemplo, con una cinta métrica) y luego la divides por el diámetro, siempre obtienes el mismo número. Este número es inusual porque no se puede escribir como una fracción simple o decimal. En su lugar, podemos redondearlo a un número como 3,14, que es "suficientemente bueno".

4. Escribe la definición de π como un problema de álgebra. Como se explicó anteriormente, π solo significa `el número que obtienes cuando divides la circunferencia por el diámetro`. En forma de fórmula matemática esto es: π = circunferencia / diámetro o π = C / re.

5. Cambia este problema para que resuelvas este problema para el perímetro C. Queremos saber cuál es el perímetro, por lo que necesitamos obtener C en un solo lado. Haz esto multiplicando cada lado de la ecuación por d:

6. Sustituye los números y resuelve para C. Regrese al problema original para ver cuál es el diámetro y reemplace la d en esta ecuación con ese número. Reemplace π con un redondeo como 3.14, o use el botón π en su calculadora para obtener un resultado más preciso. Multiplique los valores y d juntos y obtendrá el perímetro C.
Método 3 de 4: Encontrar el perímetro usando el área

1. Entender cómo se calcula el área de un círculo. Por lo general, el área (a) de un círculo no medido directamente. En su lugar, mide el radio (r) del círculo, y luego calcula el área con la fórmula A = r. La razón por la que esta fórmula tiene sentido es un poco difícil de explicar, pero puedes aprender más a través de este enlace si está interesado y dispuesto a llegar al fondo de un poco de álgebra más pesada.
- Observación: Si el problema matemático no menciona el área del círculo, es posible que deba usar un método diferente al de este artículo.

2. Aprende una fórmula para calcular la circunferencia. la circunferencia (C) es la distancia alrededor del círculo. Generalmente calculas esto con la fórmula C=2πr, pero como aún no sabemos cuál es el radio (r), tendremos que dedicar algún tiempo a averiguar el valor de r antes de que podamos resolver la ecuación.

3. Usa la fórmula del área para obtener r en un lado. Como A = πr, podemos reorganizar esta fórmula para resolver r en su lugar. Si encuentra que los pasos a continuación son difíciles de seguir, es posible que desee probar primero algunos problemas de álgebra más simples o practicar algunas técnicas para comprender el álgebra.

4. Cambia la fórmula del perímetro usando lo que encontraste. Cada vez que tienes una ecuación como r = √(A/π), ¿Puedes reemplazar un lado de la ecuación con el otro?. Usemos esta técnica para obtener la fórmula de la circunferencia anterior, C=2πr, cambiar. Para este problema no sabemos el valor de r, pero si sabemos el de A. Cambiémoslo así para que el problema se pueda resolver:

5. Sustituye los números para encontrar el perímetro. Usa el área dada en el problema para encontrar el perímetro del perímetro. Por ejemplo, si el área (a) de un círculo es de 15 unidades cuadradas, luego complete 2π(√(15/π)) en tu calculadora. No olvides los paréntesis.
Método 4 de 4: Determinar la circunferencia de un círculo real

1. Utilice este método para medir objetos circulares reales. Puedes medir la circunferencia de los círculos que encuentres en el mundo real, no solo en los problemas. Pruébalo en una rueda de bicicleta, una pizza o una moneda.

2. Toma un trozo de cuerda y una regla. La cuerda debe ser lo suficientemente larga para envolver el círculo una vez y lo suficientemente flexible para que quede ajustada. Necesitarás algo para medir la cuerda más tarde, como una regla o una cinta métrica. La cuerda será más fácil de medir si la regla es más larga que la longitud de la cuerda.

3. Envuelve la cuerda una vez alrededor del círculo. Comience colocando un extremo de la cuerda a lo largo del borde del círculo. Enrolle la cuerda alrededor del círculo y tire con fuerza. Si mide una moneda u otro objeto delgado, es posible que no pueda tensar la cuerda alrededor de él. Coloque el objeto circular plano y coloque la cuerda alrededor de él, lo más apretado posible.

4. Marcar o cortar la cuerda. Encuentra el lugar en la cuerda donde termina el lazo y toca el extremo de la cuerda con la que comenzaste. Marque este lugar con un marcador o corte la cuerda en este lugar.

5. Afloja la cuerda y mídela con una regla. Tome la cuerda envuelta y mídala con una regla. Si usó un marcador, mida solo desde el final de la cuerda hasta el marcador. Esta es la parte de la cuerda que se enrolla alrededor del círculo, y dado que la circunferencia de un círculo es solo la distancia alrededor del círculo, encontraste la respuesta! La longitud de esta cuerda es igual a la circunferencia del círculo.
Consejos
- Puedes escribir el plural de radio como radios o como radios.
Artículos sobre el tema. "Encontrar la circunferencia de un círculo"
Оцените, пожалуйста статью
Similar
Popular