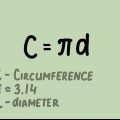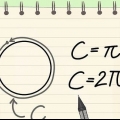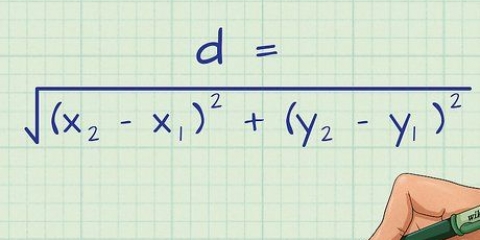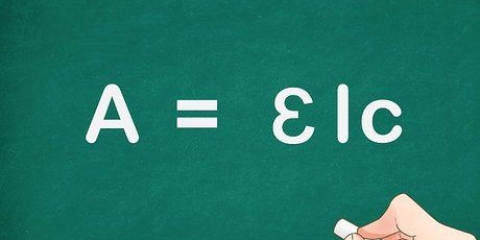Cómo calcular el radio de un círculo

Contenido

Pasos

El radio de un círculo es la distancia desde el centro del círculo hasta el borde. El diámetro de un círculo es la longitud de la línea recta que se puede trazar entre dos puntos de la esfera o círculo y que pasa por su centro.A menudo se le pide que calcule el radio de un círculo en función de otros datos. En este artículo aprenderás a calcular el radio de un círculo en función de un diámetro, una circunferencia y un área determinados. El cuarto método es un método más avanzado para determinar el centro y el radio de un círculo en función de las coordenadas de tres puntos del círculo.

Pasos

Método 1 de 3: calcula el radio si conoces el diámetro

Imagen titulada Calcular el radio de un círculo Paso 1

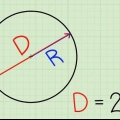
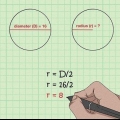
1. Recuerda cual es el diametro. El diámetro de un círculo es la longitud de la línea recta que se puede trazar entre dos puntos de la esfera o círculo y que pasa por su centro. El diámetro es la línea más larga que se puede dibujar a través de un círculo y divide el círculo en dos mitades. La longitud del diámetro también es igual a la longitud del doble del radio. La fórmula para el diámetro es la siguiente: D= 2r, donde "D" significa diámetro y "r" para viga. La fórmula para el radio se puede derivar de la fórmula anterior y por lo tanto es: r = D/2.

Imagen titulada Calcular el radio de un círculo Paso 2

2. Divide el diámetro entre 2 para encontrar el radio. Si conoce el diámetro de un círculo, todo lo que necesita hacer es dividirlo por 2 para encontrar el radio.

Por ejemplo, si el diámetro de un círculo es 4, entonces la recta es 4/2, o 2.

Método 2 de 3: calcula el radio si conoces la circunferencia

Imagen titulada Calcular el radio de un círculo Paso 3

1. ¿Recuerdas la fórmula de la circunferencia de un círculo?. La circunferencia de un círculo es la distancia alrededor del círculo. Otra forma de verlo es esta: el perímetro es la longitud de la línea que obtienes si abres el círculo en un punto y colocas la línea recta. La fórmula para la circunferencia de un círculo es O = 2πr, donde "r" es el radio y π es la constante pi, o 3.14159... La fórmula para el radio es entonces r = O/2π.

Por lo general, puedes redondear pi a dos dígitos después del punto decimal (3,14), pero primero consulta con tu maestro.

Imagen titulada Calcular el radio de un círculo Paso 4

2. Calcular el radio con la circunferencia dada. Para calcular el radio basado en la circunferencia, divide la circunferencia por 2π, o 6,28

Por ejemplo, si la circunferencia es 15, entonces el radio es r = 15/2π, o 2,39.

Método 3 de 3: calcula el radio si conoces las coordenadas de tres puntos en el círculo

Imagen titulada Calcular el radio de un círculo Paso 9

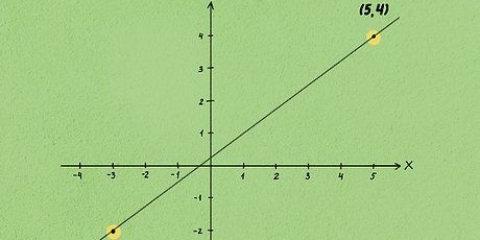
1. Comprender que tres puntos pueden definir un círculo. Cualquier tres puntos en una cuadrícula definen un círculo tangente a los tres puntos. Es la circunferencia circunscrita al triángulo que forman los puntos. El centro del círculo puede caer dentro o fuera del triángulo, según la posición de los tres puntos, y al mismo tiempo es el "intersección" del triangulo.Es posible calcular el radio del círculo si conoces las coordenadas xy de los tres puntos en cuestión.

Como ejemplo, tomemos tres puntos definidos de la siguiente manera: P1 = (3,4), P2 = (6, 8) y P3 = (-1, 2).

Imagen titulada Calcular el radio de un círculo Paso 10

2. Usa la fórmula de la distancia para calcular las longitudes de los tres lados del triángulo, que llamamos a, b y c. La fórmula para la distancia entre dos coordenadas (x₁, y₁) y (x₂, y₂) es como sigue: distancia = √(( x₂ - X₁) + (y₂ - y₁)). Ahora procesa las coordenadas de los tres puntos en esta fórmula para encontrar las longitudes de los tres lados del triángulo.

Imagen titulada Calcular el radio de un círculo Paso 11

3. Calcula la longitud del primer lado a, que va del punto P1 al P2. En nuestro ejemplo, las coordenadas de P1 (3,4) y de P2 (6,8), por lo que la longitud del lado a = √((6 - 3) + (8 - 4)).

a = √(3 + 4)

a = √(9 + 16)

a = √25

un = 5

Imagen titulada Calcular el radio de un círculo Paso 12

4. Repite el proceso para encontrar la longitud del segundo lado b, que va de P2 a P3. En nuestro ejemplo, las coordenadas de P2 (6,8) y de P3 son (-1,2), por lo que la longitud del lado b = √((-1 - 6) + (2 - 8)).

b= √(-7 + -6)

segundo = √(49 + 36)

b = √85

b = 9.23

Imagen titulada Calcular el radio de un círculo Paso 13

5. Repite el proceso para encontrar la longitud del tercer lado c, que va de P3 a P1. En nuestro ejemplo, las coordenadas de P3 (-1,2) y de P1 (3,4), por lo que la longitud del lado c =√((3 - -1) + (4 - 2)).

c= √(4 + 2)

c = √(16 + 4)

c = √20

c = 4.47

Imagen titulada Calcular el radio de un círculo Paso 14

6. Use estas longitudes en la fórmula para encontrar el radio: (abc)/(√(a + b + c)(b + c - a)(c + a - b)(a + b - c)).. El resultado es el radio de nuestro círculo!

Las longitudes del triángulo son las siguientes: a = 5, b = 9.23 y c = 4.47. Así que la fórmula para el radio se ve así: r = (5 * 9.23*4.47)/(√(5 + 4.47 + 9.23)(4.47 + 9.23 - 5)(9.23 + 5 - 4.47)(5 + 4.47 – 9.23)).