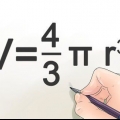Cómo calcular el radio de una esfera

Contenido

Pasos
Consejos

El radio de una esfera (abreviado como la variable r o R) es la distancia desde el centro exacto de la esfera hasta un punto en la superficie de esa esfera. Al igual que círculos, el radio de una esfera es a menudo un primer dato esencial para el cálculo del diámetro, la circunferencia, el área y el volumen de una esfera. Sin embargo, también puede trabajar hacia atrás desde el diámetro, la circunferencia, etc. para encontrar el radio de la esfera. Use la fórmula que sea apropiada para los datos que tiene.

Pasos

Método 1 de 3: usar fórmulas de radio

Imagen titulada Encuentra el radio de una esfera Paso 1

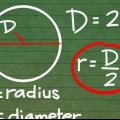
1. Determina el radio si conoces el diámetro. El radio es la mitad de un diámetro, entonces usas la fórmula r = D/2. Este es idéntico al método para calcular el radio de un círculo dado el diámetro.

Si tienes una esfera con un diámetro de 16 cm, calculas el radio con 16/2 = 8cm. Si el diámetro es 42, entonces el radio 21.

Imagen titulada Encuentra el radio de una esfera Paso 2

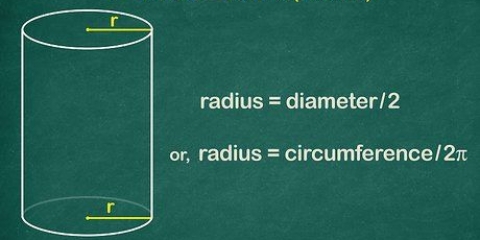
2. Determina el radio si conoces la circunferencia. Usa la fórmula C/2π. Como la circunferencia es igual a πD, que a su vez es igual a 2πr, calculas el radio dividiendo la circunferencia por 2π.

Si tienes una esfera con una circunferencia de 20 m, encontrarás el radio con 20/2π = 3,183 metros.

Puede usar la misma fórmula para convertir entre el radio y la circunferencia de un círculo.

Imagen titulada Encuentra el radio de una esfera Paso 3

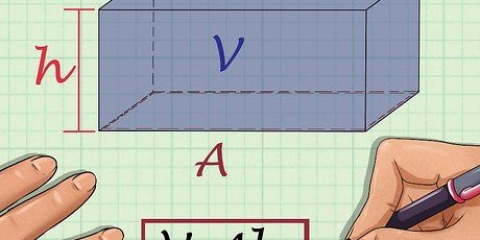
3. Calcula el radio si conoces el volumen de la esfera. Usa la fórmula ((V/π)(3/4)). El volumen de una esfera se deriva de la ecuación V = (4/3)πr.Al resolver la ecuación para r, obtienes ((V/π)(3/4)) = r, por lo que queda claro que el radio de una esfera es igual al volumen dividido por π, multiplicado por 3/4, a la 1/3 de potencia (o raíz cúbica).

Si tienes una esfera con un volumen de 100 cm, obtienes el radio de la siguiente manera:

((V/π)(3/4)) = r

((100/π)(3/4)) = r

((31.83)(3/4)) = r

(23.87) = r

2.88 = r

Imagen titulada Encuentra el radio de una esfera Paso 4

4. Determinar el radio de la superficie. Usa la fórmula r = √(A/(4π)). El área de una esfera se calcula mediante la ecuación A = 4πr. Resolviendo la ecuación para r da √(A/(4π)) = r, lo que significa que el radio de una esfera es igual a la raíz cuadrada de su área dividida por 4π. También puede potenciar (A/(4π)) a 1/2 para obtener el mismo resultado.

Si tienes una esfera con un área de 1200 cm, calculas el radio de la siguiente manera:

√(A/(4π)) = r

√(1200/(4π)) = r

√(300/(π)) = r

√(95.49) = r

9,77cm = r

Método 2 de 3: definición de términos clave

Imagen titulada Encuentra el radio de una esfera Paso 5

1. Conocer las dimensiones básicas de una esfera. El radio (r) es la distancia desde el centro exacto de la esfera hasta cualquier punto de la superficie de la esfera. En general, puedes encontrar el radio de una esfera si conoces su diámetro, circunferencia, volumen o área.

Diámetro (D): la longitud de la línea que pasa por el centro de una esfera & ndash; doblar el radio. El diámetro es la longitud de una línea que pasa por el centro de la esfera: desde un punto en el exterior de la esfera hasta el punto correspondiente directamente opuesto a ella. En otras palabras, la mayor distancia posible entre dos puntos de la esfera.
Circunferencia (C): la distancia unidimensional alrededor de la esfera en su punto más ancho. En otras palabras, el perímetro de la sección transversal circular de una esfera cuyo plano pasa por el centro de la esfera.
Volumen (V): el espacio tridimensional dentro de la esfera. Es el "espacio ocupado por la esfera".
Área (A): el espacio bidimensional en la superficie exterior de la esfera. La cantidad de espacio plano que cubre el exterior de la esfera.
pi (π): una constante que expresa la relación entre la circunferencia del círculo y el diámetro del círculo. Los primeros 10 dígitos de Pi son siempre 3.141592653, aunque esto generalmente se redondea a 3.14.

Imagen titulada Encuentra el radio de una esfera Paso 6

2. Use diferentes lecturas para determinar el radio. Puedes usar el diámetro, el perímetro, el volumen y el área para calcular el radio de una esfera. Si conoces la longitud del radio, puedes calcular cualquiera de estos números. Entonces, para encontrar el radio, puedes invertir las fórmulas para calcular estas partes. Aprende las fórmulas que involucran el radio para calcular el diámetro, la circunferencia, el área y el volumen.

D = 2r. Al igual que círculos es el diametro de una esfera el doble de su radio.

C = πD o 2πr. Al igual que círculos es la circunferencia de una esfera igual a π veces el diámetro. Como el diámetro es el doble del radio, también podemos decir que la circunferencia es igual al doble del radio por π.

V = (4/3)πr. El volumen de una esfera es su radio al cubo (r x r x r), multiplicado por π, multiplicado por 4/3.

A = 4πr. El área de una esfera es su radio elevado a la segunda potencia (r x r), por π, por 4. Dado que la circunferencia de un círculo es igual a πr, también se puede decir que el área de una esfera es igual a cuatro veces el área de un círculo, formado por su circunferencia.

Método 3 de 3: encontrar el radio como la distancia entre dos puntos

Imagen titulada Encuentra el radio de una esfera Paso 7

1. Determinar las coordenadas (x, y, z) del centro de la esfera. Una forma de pensar en el radio de una esfera es como la distancia entre el centro de la esfera y cualquier punto de su superficie. Dado que esto es cierto, puede determinar el radio de la esfera usando las coordenadas del centro y un punto en la superficie de la esfera, calculando la distancia entre los dos puntos usando una variante de la fórmula de distancia estándar. Para empezar, encuentra las coordenadas del centro de la esfera. Tenga en cuenta que una esfera es tridimensional, será un punto (x, y, z) en lugar de un punto (x, y).

Esto es más fácil de entender con un ejemplo. Supongamos que se da una esfera con centro(-1, 4, 12). En los próximos pasos vamos a utilizar este punto para determinar el radio.

Imagen titulada Encuentra el radio de una esfera Paso 8

2. Determinar las coordenadas de un punto en la superficie de la esfera. Luego necesitas determinar las coordenadas (x, y, z) de un punto en la superficie de la esfera. Esto es posible cada punto en la superficie de la esfera. Debido a que, por definición, todos los puntos en la superficie de una esfera son equidistantes del centro, puede usar cualquier punto para determinar el radio.

En el contexto de nuestra tarea de ejemplo, afirmamos que el punto (3, 3, 0) en la superficie de la esfera, se da. Calculando la distancia entre este punto y el centro, podemos encontrar el radio.

Imagen titulada Encuentra el radio de una esfera Paso 9

3. Determinar el radio con la fórmula d = √((x₂ - X₁) + (y₂ - y₁) + (z₂ - z₁)). Ahora que conoces el centro de la esfera y un punto en la superficie de la esfera, puedes encontrar el radio calculando la distancia entre ellos. Utilice la fórmula de la distancia tridimensional d = √((x₂ - X₁) + (y₂ - y₁) + (z₂ - z₁)), donde d es la distancia, (x₁,y₁,z₁) representa las coordenadas del punto central, y (x₂,y₂,z₂) representa las coordenadas del punto en la superficie, para determinar la distancia entre ambos puntos.

En nuestro ejemplo sustituimos (4, -1, 12) por (x₁,y₁,z₁) y (3, 3, 0) para (x₂,y₂,z₂), donde lo resolvemos de la siguiente manera:

re = √((x₂ - X₁) + (y₂ - y₁) + (z₂ - z₁))

re = √((3 - 4) + (3 - -1) + (0 - 12))

re = √((-1) + (4) + (-12))

re = √(1 + 16 + 144)

re = √(161)

d = 12,69. Este es el radio de nuestra esfera.

Imagen titulada Encuentra el radio de una esfera Paso 10

4. Sepa que, en general, r = √((x₂ - X₁) + (y₂ - y₁) + (z₂ - z₁)). En una esfera, todos los puntos de la superficie están a la misma distancia del centro de la esfera. Tomemos la fórmula de distancia tridimensional anterior y reemplacemos la variable "D" por la variable "r" del radio, entonces obtenemos una ecuación que nos permite encontrar el radio en cualquier centro dado (x₁,y₁,z₁) y cualquier punto correspondiente en la superficie (x₂,y₂,z₂).

Al elevar al cuadrado ambos lados de esta ecuación obtenemos: r = (x₂ - X₁) + (y₂ - y₁) + (z₂ - z₁). Nota: esto es esencialmente equivalente a la ecuación estándar para una esfera (r = x + y + z), asumiendo que su centro es igual a (0,0,0).

Consejos

El orden de las operaciones importa. Si no está seguro de cómo funcionan las reglas matemáticas y su calculadora admite paréntesis, asegúrese de usarlas.
Este artículo fue creado porque este tema tenía una gran demanda. Sin embargo, si está tratando de comprender la geometría espacial por primera vez, probablemente sea mejor comenzar con el otro lado: calcular las propiedades de una esfera cuando se da su radio.
Pi o π es una letra griega que indica la relación entre el diámetro de un círculo y su circunferencia. Es un número irracional y no se puede escribir como una razón de números reales. Hay muchas aproximaciones, y 333/106 da pi con cuatro decimales. Hoy en día, la mayoría de la gente recuerda la aproximación 3.14, que suele ser lo suficientemente precisa para los propósitos cotidianos.