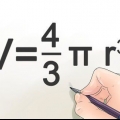Calcular la masa de una esfera: 13 pasos (con fotos)

Contenido

Pasos
Consejos

En pocas palabras, una esfera es una bola redonda sólida. Para calcular la masa de una esfera, necesitas saber el tamaño (volumen) de la esfera y su densidad. Puedes calcular el volumen usando el radio, la circunferencia o el diámetro de la esfera. También puedes sumergir la esfera en agua para encontrar el volumen por desplazamiento de agua. Si conoces el volumen, puedes multiplicarlo por la densidad para encontrar la masa.

Pasos

Parte 1 de 3: Determinar el volumen de una esfera

Imagen titulada Calcular la masa de una esfera Paso 1

1. Usa la fórmula para el volumen de una esfera. Una esfera es un sólido circular en tres dimensiones. La fórmula principal para el volumen de una esfera es:

$Volumen = \frac{4}{3} π r^{3}$ ${displaystyle {text{Volumen}}={frac {4}{3}}pi r^{3}}$

$π = 3, 14$ ${ estilo de visualización pi = 3,14}$
$r = radio$ ${displaystyle r={text{radio}}}$

Imagen titulada Calcular la masa de una esfera Paso 2

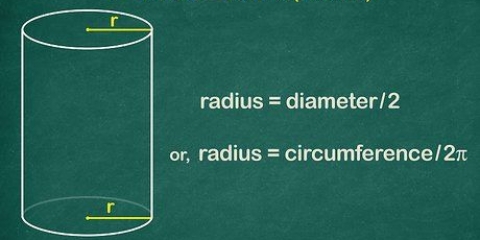
2. Halla el volumen de una esfera si conoces su radio. El radio de una esfera es la medida desde el centro de la esfera hasta el borde exterior. Si se le presenta un problema para calcular el volumen, entonces el radio probablemente esté dado. De lo contrario, el radio puede ser difícil de medir porque no se puede determinar con precisión el centro de un objeto sólido.

Suponga que le dicen que hay una esfera con un radio de 10 cm. Encuentre el volumen de la siguiente manera:

Volumen = \frac{4}{3} π r^{3}

${displaystyle {text{Volumen}}={frac {4}{3}}pi r^{3}}$

Volumen = \frac{4}{3} * (3, 14) * 10^{3}

${displaystyle {text{Volumen}}={frac {4}{3}}*(3,14)*10^{3}}$

Volumen = 4, 18667 * 1000

${displaystyle {text{Volumen}}=4.18667*1000}$

Volumen = 4186, 67 {cm}^{3}

${displaystyle {text{Volumen}}=4186,67{text{cm}}^{3}}$

Imagen titulada Calcular la masa de una esfera Paso 3

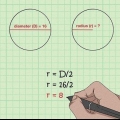
3. Determinar el volumen si se especifica el diámetro. Otra posibilidad es que para una determinada situación se dé el diámetro de una esfera. El diámetro es igual al doble del radio. De hecho, el diámetro es la distancia desde un borde de la esfera a través del centro hasta el otro borde. Para calcular el volumen a partir del diámetro (d), revise la fórmula de la siguiente manera:

Volumen = \frac{4}{3} π (\frac{D}{2})^{3}

${displaystyle {text{Volumen}}={frac {4}{3}}pi ({frac {d}{2}})^{3}}$

Como ejemplo de este cálculo, determine el volumen de una esfera con un diámetro de 10 cm.

Volumen = \frac{4}{3} π (\frac{D}{2})^{3}

${displaystyle {text{Volumen}}={frac {4}{3}}pi ({frac {d}{2}})^{3}}$

Volumen = \frac{4}{3} π (\frac{10}{2})^{3}

${displaystyle {text{Volumen}}={frac {4}{3}}pi ({frac {10}{2}})^{3}}$

Volumen = \frac{4}{3} * (3, 14) * (5^{3})

${displaystyle {text{Volumen}}={frac {4}{3}}*(3,14)*(5^{3})}$

Volumen = 4, 18667 * 125

${displaystyle {text{Volumen}}=4.18667*125}$

Volumen = 523, 3 {cm}^{3}

${displaystyle {text{Volumen}}=523,3{text{cm}}^{3}}$

Imagen titulada Calcular la masa de una esfera Paso 4

4. Revisa la fórmula si conoces el perímetro. La circunferencia de una esfera es probablemente la más fácil de medir directamente. Puede usar una cinta métrica, envuélvala suavemente alrededor de la parte más ancha de la bombilla y tome la medida. Tal vez la circunferencia se da en una declaración. Para encontrar el volumen a partir del perímetro (C), revisa la fórmula de la siguiente manera:

Volumen = \frac{4}{3} π r^{3}

${displaystyle {text{Volumen}}={frac {4}{3}}pi r^{3}}$

Volumen = \frac{4}{3} π * (C 2 π)^{3}

${displaystyle {text{Volumen}}={frac {4}{3}}pi *({frac {C}{2pi }})^{3}}$

Volumen = \frac{4}{3} π * (C 3 8 π 3)

${displaystyle {text{Volumen}}={frac {4}{3}}pi *({frac {C^{3}}{8pi ^{3}}})}$

Volumen = C 3 6 π 2

${displaystyle {text{Volumen}}={frac {C^{3}}{6pi ^{2}}}}$

Imagen titulada Calcular la masa de una esfera Paso 5

5. Calcula el volumen si conoces el perímetro. Supongamos que obtienes una esfera y mides la circunferencia en 32 cm. Encuentre el volumen de la siguiente manera:

Volumen = C 3 6 π 2

${displaystyle {text{Volumen}}={frac {C^{3}}{6pi ^{2}}}}$

Volumen = 323 6 * 3, 14 2

${displaystyle {text{Volumen}}={frac{32^{3}}{6*3,14^{2}}}}$

Volumen = 32.768 59, 158

${displaystyle {text{Volumen}}={frac {32,768}{59,158}}}$

Volumen = 553, 9 {cm}^{3}

${displaystyle {text{Volumen}}=553,9{text{cm}}^{3}}$

Imagen titulada Calcular la masa de una esfera Paso 6

6. Medir el volumen por desplazamiento de agua. Un último método práctico para medir el volumen es sumergir el bulbo en agua. Debe tener un vaso de precipitados lo suficientemente grande para sumergir el bulbo con marcas de volumen precisas.

Vierta suficiente agua en la taza para cubrir el bulbo. Tenga en cuenta el volumen.

Vierta la bombilla en el agua. Tenga en cuenta que el nivel del agua está subiendo. Tenga en cuenta el nuevo volumen.

Resta el primer volumen del segundo. El resultado es el volumen de la esfera.

Suponga que su nivel de agua aumenta de 100 ml a 625 ml cuando sumerge la bombilla. Entonces el volumen es de 525 ml. Tenga en cuenta que 1 ml = 1 cm.

Parte 2 de 3: calcular la masa a partir del volumen

Imagen titulada Calcular la masa de una esfera Paso 7

1. Determinar la densidad. Para calcular la masa a partir del volumen, necesitas saber la densidad del objeto. Diferentes materiales tienen diferentes densidades. Por ejemplo, considere una esfera de espuma de poliestireno y compare su peso con el de una esfera de hierro del mismo tamaño. El hierro tiene una densidad mucho mayor y, por lo tanto, tendrá una masa mayor.

Puede buscar densidades de muchos materiales sólidos en línea, en libros de texto o en un Binas.
Por ejemplo, aquí están las densidades registradas de algunos materiales sólidos:

Aluminio = 2700 kg/m
Mantequilla = 870 kg/m
Plomo = 11.350 kg/m
Madera prensada = 190 kg/m

Imagen titulada Calcular la masa de una esfera Paso 8

2. Convierta las unidades según sea necesario. Las unidades que utilice al calcular el volumen deben coincidir con las unidades de volumen en la densidad medida. Si no, entonces tienes que convertirlos.

Todos los ejemplos de la sección anterior dieron como resultado volúmenes medidos en centímetros cúbicos. Sin embargo, la tabla de densidad indicada da densidades basadas en metros cúbicos. Como hay 100 centímetros en un metro, hay 10 centímetros cúbicos en un metro cúbico. Divida las densidades dadas por 10 para obtener la densidad en unidades de kg/cm (se hace fácilmente moviendo el punto decimal seis espacios a la izquierda).

Para los cuatro materiales enumerados anteriormente, las densidades convertidas son las siguientes:

Aluminio = 2700 kg/m = 0,0027 kg/cm

Mantequilla = 870 kg/m3 = 0,00087 kg/cm

Plomo = 11.350 kg/m = 0,01135 kg/cm

Madera prensada = 190 kg/m = 0,00019 kg/cm

Imagen titulada Calcular la masa de una esfera Paso 9

3. Multiplica el volumen por la densidad para encontrar la masa. La formula de la densidad es

Densidad = \frac{Masa}{Volumen}

${displaystyle {text{Densidad}}={frac {text{Masa}}{text{Volumen}}}}$ , como recordarás. Si reorganizas esto para encontrar la masa, la ecuación se convierte en

Densidad * Volumen = Masa

${displaystyle {text{Densidad}}*{text{Volumen}}={text{Masa}}}$ .

Usando los cuatro materiales antes mencionados, aluminio, mantequilla, plomo y madera prensada, determinas la masa de una esfera con un volumen de 500 cm.

Aluminio : 500 {cm}^{3} * 0, 0027 \frac{kg}{} cm 3 = 1, 35 kg

${displaystyle {text{Aluminio}}:500{text{ cm}}^{3}*0,0027{frac {text{kg}}{{text{cm}}^{3}} }= 1,35{texto{kg}}}$

Manteca : 500 {cm}^{3} * 0, 00087 \frac{kg}{} cm 3 = 0, 435 kg

${displaystyle {text{Mantequilla}}:500{text{ cm}}^{3}*0,00087{frac {text{kg}}{{text{cm}}^{3}} }= 0,435{texto{kg}}}$

Guiar : 500 {cm}^{3} * 0, 01135 \frac{kg}{} cm 3 = 5, 675 kg

${displaystyle {text{Plomo}}:500{text{ cm}}^{3}*0,01135{frac {text{kg}}{{text{cm}}^{3}} }= 5,675{text{kg}}}$

Madera prensada : 500 {cm}^{3} * 0, 00019 \frac{kg}{} cm 3 = 0, 095 kg

${displaystyle {text{Madera prensada}}:500{text{ cm}}^{3}*0,00019{frac {text{kg}}{{text{cm}}^{3} }} =0,095{texto{kg}}}$

Parte 3 de 3: Resolver un problema de muestra

Imagen titulada Calcular la masa de una esfera Paso 10

1. Lee atentamente la tarea. Cuando responda problemas con cálculos de masa, lea todo el enunciado cuidadosamente. Mientras lee, puede ser útil resaltar la entrada. Lea todo el problema cuidadosamente para ver qué se le pedirá que resuelva. Por ejemplo, considere el siguiente problema:

Una gran esfera de latón macizo tiene un diámetro de 1,2 m. Determinar la masa de la esfera.

Imagen titulada Calcular la masa de una esfera Paso 11

2. Organizar los datos conocidos y desconocidos. Si lee atentamente la declaración, puede determinar que se da el diámetro, así que use la fórmula modificada:

Volumen = \frac{4}{3} π (\frac{D}{2})^{3}

${displaystyle {text{Volumen}}={frac {4}{3}}pi ({frac {d}{2}})^{3}}$

También leíste que la esfera está hecha de latón. Debe buscar la densidad del latón en sus Binas o de otra fuente.

En el sitio web, EngineeringToolbox.com, puedes buscar que la densidad del latón es de 8480 kg/m. Dado que el diámetro de la esfera se da en metros, su volumen se calcula en metros cúbicos, por lo que no es necesario convertir la densidad.

Imagen titulada Calcular la masa de una esfera Paso 12

3. Calcular el volumen. Para calcular el volumen, ingrese la fórmula adecuada, complete los datos que conoce y realice los cálculos de la siguiente manera:

Volumen = \frac{4}{3} π (\frac{D}{2})^{3}

${displaystyle {text{Volumen}}={frac {4}{3}}pi ({frac {d}{2}})^{3}}$

Volumen = \frac{4}{3} π (1, 2 2)^{3}

${displaystyle {text{Volumen}}={frac {4}{3}}pi ({frac {1,2}{2}})^{3}}$

Volumen = 4, 18667 * 0, 6^{3}

${displaystyle {text{Volumen}}=4,18667*0,6^{3}}$

Volumen = 4, 18667 * 0, 216

${displaystyle {text{Volumen}}=4,18667*0,216}$

Volumen = 0, 90432 {metro}^{3}

${displaystyle {text{Volumen}}=0,90432{text{ m}}^{3}}$

Imagen titulada Calcular la masa de una esfera Paso 13

4. Usa la densidad para calcular la masa. Piensa eso

Masa = Densidad * Volumen

${displaystyle {text{Masa}}={text{Densidad}}*{text{Volumen}}}$ . Ingrese los valores que conoce en la fórmula para encontrar la masa:

Masa = Densidad * Volumen

${displaystyle {text{Masa}}={text{Densidad}}*{text{Volumen}}}$

Masa = 8480 \frac{kg}{} metro 3 * 0, 90432 {metro}^{3}

${displaystyle {text{Masa}}=8480{frac {text{ kg}}{{text{ m}}^{3}}}*0,90432{text{ m}}^{3 }}$

Masa = 7668, 6 kg

${displaystyle {text{Masa}}=7668,6{text{ kg}}}$

Consejos

Esta explicación asume que la densidad de la esfera es la misma en todas partes. Esto se supone en la mayoría de los problemas matemáticos y físicos. Sin embargo, es posible que el núcleo de una esfera esté hecho de un material diferente al de la superficie.