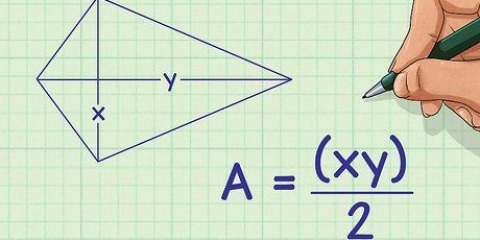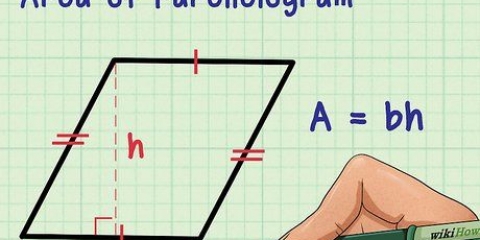Por ejemplo, si el volumen del prisma es 64  ), su fórmula se verá así:
), su fórmula se verá así:


Por ejemplo, si la base es un rectángulo de 8 metros de largo y 2 metros de ancho, calcularías el área de la siguiente manera:



Por ejemplo, si calculaste que el área de la base es 16 m, tu fórmula se verá así:


Por ejemplo, en la ecuación  , tienes que dividir cada lado por 16 om
, tienes que dividir cada lado por 16 om  calcular. Por lo tanto:
calcular. Por lo tanto:


entonces la altura del prisma rectangular es de 4 metros. 

Por ejemplo, si sabes que el volumen del prisma es de 840 metros cúbicos ( ), su fórmula se verá así:
), su fórmula se verá así:


Si conoce la longitud de los tres lados de un triángulo, puede calcular el área utilizando la fórmula de Heron.leer Calcular el area de un triangulo para instrucciones detalladas. Por ejemplo, si la base del triángulo mide 12 metros y la altura del triángulo mide 7 metros, entonces encuentra el área de la siguiente manera:




Por ejemplo, si sabes que el área de la base es de 42 m2, tu fórmula se verá así:


Por ejemplo, en la ecuación  , debes dividir cada lado por 42 para determinar
, debes dividir cada lado por 42 para determinar  . Por lo tanto:
. Por lo tanto:


Entonces, la altura de tu prisma triangular es de 20 metros. 

Por ejemplo, si el área es 1460 cm, tu fórmula se vería así:


Por ejemplo, si la base es un rectángulo con una longitud de 8 cm y un ancho de 2 cm, encuentre el área de la siguiente manera:



Por ejemplo, si el área de la base es 16, tu fórmula quedaría así:



Recuerda que los lados opuestos de un rectángulo tienen la misma longitud. Por ejemplo, si la base es un rectángulo de 8 cm de largo y 2 cm de ancho, encuentra el perímetro de la siguiente manera:



Por ejemplo, si el perímetro de la base es 20, tu fórmula se vería así:


Por ejemplo, en la ecuación  primero resta 32 de cada lado, luego divide cada lado por 20. Por lo tanto:
primero resta 32 de cada lado, luego divide cada lado por 20. Por lo tanto:




Entonces la altura de tu prisma es 71.4 cm. 

Por ejemplo, si el área es 1460 cm, tu fórmula se vería así:


Si conoce la longitud de los tres lados de un triángulo, puede determinar el área utilizando la fórmula de Heron.leer Calcular el area de un triangulo para instrucciones completas. Por ejemplo, si la base del triángulo es de 8 cm y la altura del triángulo es de 4 cm, calcularías el área de la siguiente manera:




Por ejemplo, si el área de la base es 16, tu fórmula quedaría así:



Por ejemplo, si la base es un triángulo con longitudes de 8, 4 y 9 cm, calculas el perímetro de la siguiente manera:



Por ejemplo, suponga que el perímetro de la base es 21, su fórmula se verá así:


Por ejemplo, en la ecuación  , primero debes restar 32 de cada lado, luego dividir cada lado por 21. Por lo tanto:
, primero debes restar 32 de cada lado, luego dividir cada lado por 21. Por lo tanto:




Entonces, la altura de tu prisma es de 68 cm.
Calcular la altura de un prisma
Contenido
- Pasos
- Método 1 de 4: encontrar la altura de un prisma rectangular de volumen conocido
- Método 2 de 4: Determinar la altura de un prisma triangular de volumen conocido
- Método 3 de 4: Encontrar la altura de un prisma rectangular usando su área
- Método 4 de 4: determina la altura de un prisma triangular usando su área
- Artículos de primera necesidad
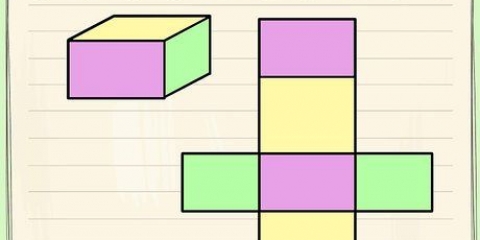
Un prisma es una figura tridimensional con dos bases paralelas, que son congruentes.La forma de la base determina qué tipo de prisma es, como un prisma rectangular o triangular. Dado que es una forma 3D, no es raro querer calcular el volumen de un prisma; sin embargo, necesitas la altura del prisma para eso. Encontrar la altura es posible cuando se ha recibido suficiente información: ya sea el volumen, el área y el perímetro de la base. Las fórmulas descritas en los métodos a continuación son adecuadas para prismas con bases de cualquier forma, siempre que conozca la fórmula para encontrar el área de esa forma.
Pasos
Método 1 de 4: encontrar la altura de un prisma rectangular de volumen conocido

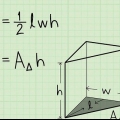
1. Usa la fórmula para el volumen de un prisma. El volumen de un prisma se puede encontrar usando la fórmula  , por lo cual
, por lo cual  es igual al volumen del prisma,
es igual al volumen del prisma,  es igual al área de una base, y
es igual al área de una base, y  es igual a la altura del prisma.
es igual a la altura del prisma.
 , por lo cual
, por lo cual  es igual al volumen del prisma,
es igual al volumen del prisma,  es igual al área de una base, y
es igual al área de una base, y  es igual a la altura del prisma.
es igual a la altura del prisma. - La base de un prisma es uno de sus lados congruentes. Dado que todos los lados opuestos de un prisma rectangular son congruentes, cualquier lado puede usarse como plano de tierra, siempre que sea consistente con sus cálculos.

2. Aplicar el volumen a la fórmula. Si no conoce el volumen, no puede usar este método.
 ), su fórmula se verá así:
), su fórmula se verá así:

3. Halla el área de la base. Para encontrar el área, necesitas saber el largo y el ancho de la base (o de un lado, si la base es un cuadrado). Usa la fórmula  para determinar el area de un rectangulo.
para determinar el area de un rectangulo.
 para determinar el area de un rectangulo.
para determinar el area de un rectangulo.


4. Sustituir el área de la base en el volumen de la fórmula del prisma. Asegúrese de sustituir la variable  .
.
 .
.

5. Resuelva la ecuación para h  . Ahora sabes la altura de tu prisma.
. Ahora sabes la altura de tu prisma.
 . Ahora sabes la altura de tu prisma.
. Ahora sabes la altura de tu prisma. , tienes que dividir cada lado por 16 om
, tienes que dividir cada lado por 16 om  calcular. Por lo tanto:
calcular. Por lo tanto:

entonces la altura del prisma rectangular es de 4 metros.
Método 2 de 4: Determinar la altura de un prisma triangular de volumen conocido

1. Escribe la formula del volumen de un prisma. El volumen de cualquier prisma se puede encontrar usando la fórmula  ,por lo cual
,por lo cual  es igual al volumen del prisma,
es igual al volumen del prisma,  es igual al área de una base, y
es igual al área de una base, y  es igual a la altura del prisma.
es igual a la altura del prisma.
 ,por lo cual
,por lo cual  es igual al volumen del prisma,
es igual al volumen del prisma,  es igual al área de una base, y
es igual al área de una base, y  es igual a la altura del prisma.
es igual a la altura del prisma. - La base de un prisma es uno de sus lados congruentes. La base de un prisma triangular es un triangulo. los lados son rectangulos.

2. Aplicar el volumen a la fórmula. Si no conoce el volumen, no puede usar este método.
 ), su fórmula se verá así:
), su fórmula se verá así:

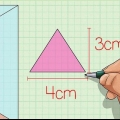
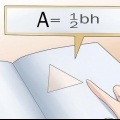
3. Halla el área de la base. Para encontrar el área, necesitas saber la longitud de la base del triángulo y la altura del triángulo. Usa la fórmula  para determinar el area de un triangulo.
para determinar el area de un triangulo.
 para determinar el area de un triangulo.
para determinar el area de un triangulo.



4. Sustituir el área de la base en el volumen de la fórmula del prisma. Asegúrese de sustituir la variable  .
.
 .
.

5. Resuelva la ecuación para h  . Ahora sabes la altura de tu prisma.
. Ahora sabes la altura de tu prisma.
 . Ahora sabes la altura de tu prisma.
. Ahora sabes la altura de tu prisma. , debes dividir cada lado por 42 para determinar
, debes dividir cada lado por 42 para determinar  . Por lo tanto:
. Por lo tanto:

Método 3 de 4: Encontrar la altura de un prisma rectangular usando su área

1. Escribe la fórmula del área de un prisma. La fórmula del área de un prisma es  , por lo cual
, por lo cual  es igual a la superficie,
es igual a la superficie,  es igual al area de la base,
es igual al area de la base,  es igual al perímetro de la base, y
es igual al perímetro de la base, y  es igual a la altura del prisma.
es igual a la altura del prisma.
 , por lo cual
, por lo cual  es igual a la superficie,
es igual a la superficie,  es igual al area de la base,
es igual al area de la base,  es igual al perímetro de la base, y
es igual al perímetro de la base, y  es igual a la altura del prisma.
es igual a la altura del prisma. - Para que este método funcione, debe conocer el área del prisma, así como la longitud y el ancho de la base.

2. Sustituye el área del prisma en la fórmula. Si se desconoce la superficie, este método no funcionará.


3. Halla el área de la base. Para encontrar el área, necesitas saber el largo y el ancho de la base (o de un lado, si la base es un cuadrado). Usa la fórmula  para determinar el area de un rectangulo.
para determinar el area de un rectangulo.
 para determinar el area de un rectangulo.
para determinar el area de un rectangulo.


4. Sustituye el área de la base en la fórmula por el área de un prisma, y simplifica. Asegúrese de completar la letra  .
.
 .
.


5. Determinar el perímetro de la base. Para encontrar el perímetro de un rectángulo, suma las longitudes de los cuatro lados, o multiplica la longitud de un lado por 4 si es un cuadrado.



6. Sustituye el perímetro de la base en la fórmula por el área de un prisma. Asegúrate de sustituir la letra  .
.
 .
.

7. Resuelva la ecuación para h  . Ahora sabes la altura de tu prisma.
. Ahora sabes la altura de tu prisma.
 . Ahora sabes la altura de tu prisma.
. Ahora sabes la altura de tu prisma. primero resta 32 de cada lado, luego divide cada lado por 20. Por lo tanto:
primero resta 32 de cada lado, luego divide cada lado por 20. Por lo tanto:



Método 4 de 4: determina la altura de un prisma triangular usando su área

1. Escribe la fórmula del área de un prisma. La fórmula del área de un prisma es  , por lo cual
, por lo cual  es igual a la superficie,
es igual a la superficie,  es igual al area de la base,
es igual al area de la base,  es igual al perímetro de la base, y
es igual al perímetro de la base, y  es igual a la altura del prisma.
es igual a la altura del prisma.
 , por lo cual
, por lo cual  es igual a la superficie,
es igual a la superficie,  es igual al area de la base,
es igual al area de la base,  es igual al perímetro de la base, y
es igual al perímetro de la base, y  es igual a la altura del prisma.
es igual a la altura del prisma. - Para que este método funcione, se debe conocer el área del prisma, así como el área de la base triangular y la longitud de los tres lados de la base.

2. Sustituye el área del prisma en la fórmula. Si no se conoce la superficie, este método no funcionará.


3. Halla el área de la base. Para encontrar el área, necesitas saber la longitud de la base del triángulo y la altura del triángulo. Usa la fórmula  para determinar el area de un triangulo.
para determinar el area de un triangulo.
 para determinar el area de un triangulo.
para determinar el area de un triangulo.



4. Sustituye el área de la base en la fórmula por el área de un prisma y simplifica. Substituto para  .
.
 .
.


5. Determinar el perímetro de la base. Para encontrar el perímetro de un triángulo, suma las longitudes de los tres lados.



6. Sustituye el perímetro de la base en la fórmula por el área de un prisma. Asegúrese de sustituir  .
.
 .
.

7. Resuelva la ecuación para h  . Ahora sabes la altura de tu prisma.
. Ahora sabes la altura de tu prisma.
 . Ahora sabes la altura de tu prisma.
. Ahora sabes la altura de tu prisma. , primero debes restar 32 de cada lado, luego dividir cada lado por 21. Por lo tanto:
, primero debes restar 32 de cada lado, luego dividir cada lado por 21. Por lo tanto:



Artículos de primera necesidad
- Bolígrafo/lápiz y papel o calculadora (opcional)
Artículos sobre el tema. "Calcular la altura de un prisma"
Оцените, пожалуйста статью
Similar
Popular