Cómo calcular la longitud de la diagonal en un rectángulo

Contenido

Pasos

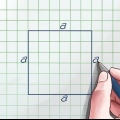
Una diagonal es una línea recta que conecta una esquina de un rectángulo con la esquina opuesta. Un rectángulo tiene dos diagonales, cada una de la misma longitud. Si conoce las longitudes de los lados de un rectángulo, es fácil encontrar la longitud de la diagonal usando el Teorema de Pitágoras, porque una diagonal divide un rectángulo en dos triángulos rectángulos. Si no sabes las longitudes de los lados, pero tienes otros datos (como el área y el perímetro, o la razón entre las longitudes de los lados), puedes medir la longitud y el ancho de los lados con un unos pocos pasos extra encuentre el rectángulo, y luego usando el teorema de Pitágoras, encuentre la longitud y el ancho de la diagonal.

Pasos

Método 1 de 3: usar el largo y el ancho

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 1

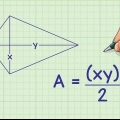
1. Escribe la fórmula del teorema de Pitágoras. la fórmula es

a 2 + B^{2} = C^{2}

$a^{{2}}+b^{{2}}=c^{{2}}$ , por lo cual

a

$a$ y

B

$B$ son iguales a las longitudes de los lados de un triángulo rectángulo, y

C

$C$ es igual a la longitud de la hipotenusa de un triángulo rectángulo.

Usas el teorema de Pitágoras porque la diagonal de un rectángulo lo divide en dos triángulos rectángulos congruentes. La longitud y el ancho del rectángulo son las longitudes de los lados del triángulo; la diagonal es la hipotenusa del triangulo.

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 2

2. Aplicar la longitud y el ancho a la fórmula. Estos son si se da correctamente, o puedes medirlos. Asegúrese de sustituir

a

$a$ y

B

$B$ .

Por ejemplo, si el ancho de un rectángulo es de 3 cm y la longitud es de 4 cm, tu fórmula se vería así:

32 + 4^{2} = C^{2}

$3^{{2}}+4^{{2}}=c^{{2}}$ .

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 3

3. Cuadre el largo y el ancho, luego sume estos números. Elevar al cuadrado es multiplicar el número por sí mismo.

Por ejemplo:

32 + 4^{2} = C^{2}

$3^{{2}}+4^{{2}}=c^{{2}}$

9 + dieciséis = C 2

$9+16=c^{{2}}$

25 = C 2

$25=c^{{2}}$

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 4

4. Resta la raíz cuadrada de cada lado de la ecuación. La forma más fácil de encontrar una raíz cuadrada es usar una calculadora. Puedes usar una calculadora en línea si no tienes una calculadora científica. Esto te da el valor

C

$C$ , o la hipotenusa del triángulo y la diagonal del rectángulo.

Por ejemplo:

25 = C 2

$25=c^{{2}}$

\sqrt{25} = \sqrt{C} 2

${sqrt{25}}={sqrt{c^{{2}}}}$

5 = C

$5=c$
Entonces, la diagonal o un rectángulo con un ancho de 3 cm y una longitud de 4 cm es de 5 cm.

Método 2 de 3: usar el área y el perímetro

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 5

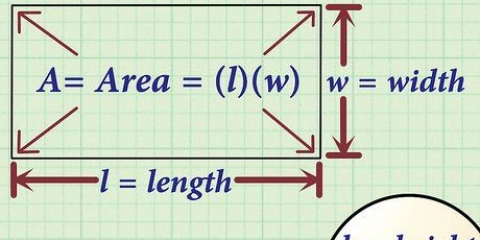
1. Escribe la formula del area de un rectangulo. la fórmula es

a = yo w

$A = bajo$ , por lo cual

a

$a$ es igual al area del rectangulo,

yo

$yo$ es igual a la longitud del rectángulo, y

w

$w$ es igual al ancho del rectangulo.

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 6

2. Usa el área del rectángulo en la fórmula. Asegúrese de sustituir la variable correcta

a

$a$ .

Por ejemplo, si el área del rectángulo es de 35 centímetros cuadrados, tu fórmula quedaría así:

35 = yo w

$35=bajo$ .

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 7

3. Reorganice la fórmula y obtendrá un valor para w{ estilo de visualización w} $w$ . Esto se hace dividiendo ambos lados de la ecuación por

yo

$yo$ . Ponga este valor a un lado. Usará esto más adelante en la fórmula para el perímetro.

Por ejemplo:

35 = yo w

$35=bajo$

\frac{35}{yo} = w

${frac{35}{l}}=w$ .

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 8

4. Escribe la fórmula del perímetro de un rectángulo. la fórmula es

pags = 2 (w + yo)

$P=2(w+1)$ , por lo cual

w

$w$ es igual al ancho del rectángulo, y

yo

$yo$ es igual a la longitud del rectángulo.

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 9

5. Usa el valor del perímetro en la fórmula. Asegúrese de sustituir la variable

pags

$pags$ .

Por ejemplo, si el perímetro de un rectángulo es de 24 centímetros, tu fórmula se vería así:

24 = 2 (w + yo)

$24=2(an+l)$ .

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 10

6. Divide ambos lados de la ecuación por 2. Esto te da el valor

w + yo

$w+l$ .

Por ejemplo:

24 = 2 (w + yo)

$24=2(an+l)$

\frac{24}{2} = 2 (w + yo) 2

${frac{24}{2}}={frac{2(w+l)}{2}}$

12 = w + yo

$12=w+l$ .

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 11

7. Usa el valor w{ estilo de visualización w} $w$ en la ecuacion. Usa el valor que encontraste al reorganizar la fórmula del área.

Por ejemplo, si encontró con la fórmula del área que

\frac{35}{yo} = w

${frac{35}{l}}=w$ , luego reemplazas el valor

w

$w$ en la fórmula circunferencial:

12 = w + yo

$12=w+l$

12 = \frac{35}{yo} + yo

$12={frac{35}{l}}+l$

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 12

8. Eliminar la fracción en la ecuación. Lo haces multiplicando ambos lados de la ecuación por

yo

$yo$ .

Por ejemplo:

12 = \frac{35}{yo} + yo

$12={frac{35}{l}}+l$

12 \times yo = (\frac{35}{yo} \times yo) + (yo \times yo)

$12veces l=({frac{35}{l}}veces l)+(lveces l)$

12 yo = 35 + yo 2

$canal12=35+canal^{{2}}$

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 13

9. Establecer la ecuación igual a 0. Haces esto restando el término de primer grado de ambos lados de la ecuación.

Por ejemplo:

12 yo = 35 + yo 2

$canal12=35+canal^{{2}}$

12 yo - 12 yo = 35 + yo 2 - 12 yo

$12-12 canales = 35+ canales^{{2}}-12 canales$

0 = 35 + yo 2 - 12 yo

$0=35+canal^{{2}}-12 canales$

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 14

10. Reordenar el orden de los términos en la ecuación. Esto quiere decir que primero viene el término con el exponente, seguido del término con la variable, y finalmente la constante. Al reorganizar, preste atención a los signos positivos y negativos correctos. La ecuación ahora está ordenada como ecuación cuadrática.

Por ejemplo,

0 = 35 + yo 2 - 12 yo

$0=35+canal^{{2}}-12 canales$ se está convirtiendo

0 = yo 2 - 12 yo + 35

$0=canal^{{2}}-12canal+35$ .

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 15

11. Factorizar la ecuación cuadrática. Para obtener instrucciones detalladas sobre cómo hacer esto, lea el artículo Resolver ecuaciones cuadráticas.

Por ejemplo, la ecuación

0 = yo 2 - 12 yo + 35

$0=canal^{{2}}-12canal+35$ se puede disolver en

0 = (yo - 7) (yo - 5)

$0=(l-7)(l-5)$ .

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 16

12. Determinar los valores de yo{ estilo de visualización l} $yo$ . Esto se hace poniendo cada término a cero y resolviendo para la variable. Obtienes dos soluciones a esta ecuación. Como se trata de un rectángulo, las dos soluciones serán el ancho y el largo de su rectángulo.

Por ejemplo:

0 = (yo - 7)

$0=(l-7)$

7 = yo

$7 = l$
Y

0 = (yo - 5)

$0=(l-5)$

5 = yo

$5 = l$ .
Entonces, el largo y el ancho del rectángulo son 7 cm y 5 cm.

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 17

13. Escribe la fórmula del teorema de Pitágoras. la fórmula es

a 2 + B^{2} = C^{2}

$a^{{2}}+b^{{2}}=c^{{2}}$ , por lo cual

a

$a$ y

B

$B$ son iguales a las longitudes de los lados de un triángulo rectángulo, y

C

$C$ es igual a la longitud de la hipotenusa de un triángulo rectángulo.

Estás usando el Teorema de Pitágoras porque la diagonal de un rectángulo lo divide en dos triángulos rectángulos congruentes. El ancho y el largo del rectángulo son los largos de los lados del triángulo; la diagonal es la hipotenusa del triangulo.

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 18

14. Usa la latitud y la longitud en la fórmula. No importa qué valor use para qué variable.

Por ejemplo, si sabes que el ancho y el largo del rectángulo son 5 cm y 7 cm, tu fórmula se vería así:

52 + 7^{2} = C^{2}

$5^{{2}}+7^{{2}}=c^{{2}}$ .

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 19

15. Eleva al cuadrado la latitud y la longitud, luego suma estos números. Cuadrar significa multiplicar un número por sí mismo.

Por ejemplo:

52 + 7^{2} = C^{2}

$5^{{2}}+7^{{2}}=c^{{2}}$

25 + 49 = C 2

$25+49=c^{{2}}$

74 = C 2

$74=c^{{2}}$

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 20

dieciséis. Saca la raíz cuadrada de cada lado de la ecuación. La forma más fácil de encontrar una raíz cuadrada es usando una calculadora. Puedes usar una calculadora en línea si no tienes una calculadora científica. Esto te da el valor

C

$C$ , y esa es la hipotenusa del triangulo, y la diagonal del rectangulo.

Por ejemplo:

74 = C 2

$74=c^{{2}}$

\sqrt{74} = \sqrt{C} 2

${sqrt{74}}={sqrt{c^{{2}}}}$

8.6024 = C

$8.6024=c$
Entonces la diagonal de un rectángulo con un área de 35 cm y un perímetro de 24 cm es de aproximadamente 8,6 cm.

Método 3 de 3: usar el área y las longitudes relacionales de los lados

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 21

1. Escribe una fórmula que explique la relación entre las longitudes de los lados. Puede cambiar la longitud (

yo

$yo$ ) o el ancho (

w

$w$ ) aislar. Deja esta fórmula a un lado por un momento. Pronto lo estarás usando en la fórmula de superficie.

Por ejemplo, si sabes que el ancho de un rectángulo es 2 cm más que su largo, puedes escribir una fórmula como $w$ $w$ : $w = yo + 2$ $w=l+2$ .

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 22

2. Escribe la formula del area de un rectangulo. la fórmula es

a = yo w

$A = bajo$ , por lo cual

a

$a$ es igual al area del rectangulo,

yo

$yo$ es igual a la longitud del rectángulo, y

w

$w$ es igual al ancho del rectangulo.

Puede usar este método si conoce el perímetro del rectángulo, excepto que ahora está usando la fórmula del perímetro en lugar de la fórmula del área. La fórmula del perímetro de un rectángulo es

pags = 2 (w + yo)

$P=2(w+1)$ , por lo cual

w

$w$ es igual al ancho del rectángulo, y

yo

$yo$ es igual a la longitud del rectángulo.

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 23

3. Usa el área del rectángulo en la fórmula. Asegúrese de sustituir la variable

a

$a$ .

Por ejemplo, si el área del rectángulo es de 35 centímetros cuadrados, tu fórmula se vería como voltios:

35 = yo w

$35=bajo$ .

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 24

4. Use la fórmula relacional para la longitud (o el ancho) en la fórmula. Dado que está tratando con un rectángulo, no importa si está trabajando con variable

yo

$yo$ o

w

$w$ .

Por ejemplo, si ha encontrado que

w = yo + 2

$w=l+2$ , entonces sustituyes esta relación por

w

$w$ en la fórmula del área:

35 = yo w

$35=bajo$

35 = yo (yo + 2)

$35=l(l+2)$

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 25

5. Que sea una ecuación cuadrática. Lo haces usando la propiedad distributiva y multiplicando los términos entre paréntesis, después de lo cual estableces la ecuación igual a 0.

Por ejemplo:

35 = yo (yo + 2)

$35=l(l+2)$

35 = yo 2 + 2 yo

$35=canal^{{2}}+canal 2$

0 = yo 2 + 2 yo - 35

$0=canal^{{2}}+canal2-35$

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 26

6. Factorizar la ecuación cuadrática. Para obtener instrucciones detalladas sobre cómo hacer esto, lea el artículo Resolver ecuaciones cuadráticas.

Por ejemplo, la ecuación

0 = yo 2 + 2 yo - 35

$0=canal^{{2}}+canal2-35$ se puede disolver como

0 = (yo + 7) (yo - 5)

$0=(1+7)(1-5)$ .

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 27

7. Determinar los valores de yo{ estilo de visualización l} $yo$ . Esto se hace igualando cada término a cero y resolviendo para la variable. Encuentras dos soluciones a la ecuación.

Por ejemplo:

0 = (yo + 7)

$0=(l+7)$

- 7 = yo

$-7=canal$
Y

0 = (yo - 5)

$0=(l-5)$

5 = yo

$5 = l$ .
En este caso hay una respuesta negativa. Como la longitud de un rectángulo no puede ser negativa, sabes que la longitud debe ser de 5 cm.

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 28

8. Use el valor de la longitud (o el ancho) en su fórmula de relación. Esto te dará la longitud del otro lado del rectángulo.

Por ejemplo, si sabes que la longitud del rectángulo es de 5 cm y que la relación entre las longitudes de los lados es

w = yo + 2

$w=l+2$ , luego ingresa 5 como longitud en la fórmula:

w = yo + 2

$w=l+2$

w = 5 + 2

$w=5+2$

w = 7

$w=7$

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 29

9. Escribe la fórmula del teorema de Pitágoras. la fórmula es

a 2 + B^{2} = C^{2}

$a^{{2}}+b^{{2}}=c^{{2}}$ , por lo cual

a

$a$ y

B

$B$ son iguales a las longitudes de los lados de un triángulo rectángulo, y

C

$C$ es igual a la longitud de la hipotenusa de un triángulo rectángulo.

Usas el teorema de Pitágoras porque la diagonal de un rectángulo lo divide en dos triángulos rectángulos congruentes. El ancho y el largo del rectángulo son los largos de los lados del triángulo; la diagonal es la hipotenusa del triangulo.

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 30

10. Usa la latitud y la longitud en la fórmula. No importa qué valor use para qué variable.

Por ejemplo, si sabe que el ancho y el largo del rectángulo son iguales a 5 cm y 7 cm, su fórmula ahora se ve así:

52 + 7^{2} = C^{2}

$5^{{2}}+7^{{2}}=c^{{2}}$ .

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 31

11. Eleva al cuadrado la latitud y la longitud, luego suma estos números. Cuadrar significa multiplicar un número por sí mismo.

Por ejemplo:

52 + 7^{2} = C^{2}

$5^{{2}}+7^{{2}}=c^{{2}}$

25 + 49 = C 2

$25+49=c^{{2}}$

74 = C 2

$74=c^{{2}}$

Imagen titulada Encuentra la medida de la diagonal dentro de un rectángulo Paso 32

12. Resta la raíz cuadrada de cada lado de la ecuación. La forma más fácil de encontrar una raíz cuadrada es usando una calculadora. Puedes usar una calculadora en línea si no tienes una calculadora científica. Esto te da el valor