Cómo determinar el ancho de un rectángulo

Contenido

Pasos

Hay innumerables formas de encontrar las dimensiones faltantes de un rectángulo, y el método que utilice dependerá de los datos que tenga. Siempre que se conozca el área o el perímetro, así como la longitud de un lado del rectángulo (o la relación entre la longitud y el ancho), se puede determinar la dimensión que falta. Las propiedades de un rectángulo son tales que estos métodos pueden usarse para determinar su latitud o longitud.

Pasos

Método 1 de 4: usar el área y la longitud

Imagen titulada Encuentra el ancho de un rectángulo Paso 1

1. Escribe la formula del area de un rectangulo. la fórmula es

a = (yo) (w)

$A=(l)(w)$ , por lo cual

a

$a$ es igual al area del rectangulo,

yo

$yo$ es igual a la longitud del rectángulo, y

w

$w$ es igual al ancho del rectangulo.

El método solo funciona para un área y una longitud determinadas del rectángulo.
Esta fórmula también está disponible en la forma $a = (h) (w)$ $A=(alto)(ancho)$ , por lo cual $h$ $h$ es igual a la altura del rectángulo (en lugar de la longitud). Estos dos términos se refieren a las mismas dimensiones.

Imagen titulada Encuentra el ancho de un rectángulo Paso 2

2. Use los valores de área y longitud en la fórmula. Asegúrese de sustituir las variables correctas.

Por ejemplo, si desea encontrar el ancho de un rectángulo con un área de 24 cm y una longitud de 8 cm, su fórmula se vería así:

24 = 8 w

$24 = 8w$

Imagen titulada Encuentra el ancho de un rectángulo Paso 3

3. Resolver w{ estilo de visualización w} $w$ . Haces esto dividiendo cada lado de la ecuación por su longitud.

Por ejemplo, en la ecuación

24 = 8 w

$24 = 8w$ , dividir cada lado por 8.

24 = 8 w

$24 = 8w$

\frac{24}{8} = 8 w 8

${frac{24}{8}}={frac{8w}{8}}$

3 = w

$3=w$

Imagen titulada Encuentra el ancho de un rectángulo Paso 4

4. Anota tu respuesta final. No olvides mencionar la unidad de las lecturas.

Por ejemplo, para un rectángulo con un área de

24 C metro 2

$24cm^{{2}}$ y una longitud de

8 C metro

$8cm$ , se convierte en el ancho

3 C metro

$3cm$ .

Método 2 de 4: usar la circunferencia y la longitud

1. Escribe la fórmula del perímetro de un rectángulo. la fórmula es

pags = 2 yo + 2 w

$P=2l+2w$ , por lo cual

pags

$pags$ es igual al perimetro del rectangulo,

yo

$yo$ es igual a la longitud del rectángulo, y

w

$w$ es igual al ancho del rectangulo.

Este método solo funciona para un perímetro y una longitud determinados del rectángulo.
Esta fórmula también se escribe como $pags = 2 (w + h)$ $P=2(ancho+alto)$ , por lo cual $h$ $h$ es igual a la altura del rectángulo y se usa en lugar de la longitud. las variables $yo$ $yo$ y $h$ $h$ se refieren a las mismas dimensiones, y la propiedad distributiva dicta que estas dos fórmulas, aunque ordenadas de manera diferente, producen el mismo resultado.

Imagen titulada Encuentra el ancho de un rectángulo Paso 6

2. Usa la circunferencia y la longitud en la fórmula. Asegúrese de sustituir las variables correctas.

Por ejemplo, si quisiera encontrar el ancho de un rectángulo con una circunferencia de 22 cm y una longitud de 8 cm, la fórmula se vería así:

22 = 2 (8) + 2 w

$22=2(8)+2w$

22 = dieciséis + 2 w

$22=16+2w$

Imagen titulada Encuentra el ancho de un rectángulo Paso 7

3. Resolver w{ estilo de visualización w} $w$ . Para hacer esto, debes restar la longitud de cada lado de la ecuación y dividirla por 2.

Por ejemplo, en la ecuación

22 = dieciséis + 2 w

$22=16+2w$ , resta 16 de cada lado y divide por 2.

22 = dieciséis + 2 w

$22=16+2w$

6 = 2 w

$6=2w$

\frac{6}{2} = 2 w 2

${frac{6}{2}}={frac{2w}{2}}$

3 = w

$3=w$

Imagen titulada Encuentra el ancho de un rectángulo Paso 8

4. Anota la respuesta final. No olvides mencionar la unidad de las lecturas.

Por ejemplo, para un rectángulo con un perímetro de

22 C metro

$22cm$ y una longitud de

8 C metro

$8cm$ , se convierte en el ancho

3 C metro

$3cm$ .

Método 3 de 4: usar la diagonal y la longitud

Imagen titulada Encuentra el ancho de un rectángulo Paso 9

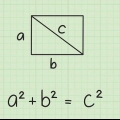
1. Escribe la formula de la diagonal de un rectangulo. la fórmula es

D = \sqrt{w} 2 + {yo}^{2}

$D={raíz cuadrada{w^{{2}}+l^{{2}}}}$ , por lo cual

D

$D$ es igual a la longitud de la diagonal,

yo

$yo$ es igual a la longitud y

w

$w$ es igual al ancho del rectangulo.

Este método solo funciona para una longitud determinada de la diagonal y la longitud de un lado del rectángulo.
Esta fórmula también se escribe como $D = \sqrt{w} 2 + h^{2}$ $D={raíz cuadrada{w^{{2}}+h^{{2}}}}$ , por lo cual $h$ $h$ es igual a la altura del rectángulo y se usa en lugar de la longitud. las variables $yo$ $yo$ y $h$ $h$ referirse a las mismas lecturas.

Imagen titulada Encuentra el ancho de un rectángulo Paso 10

2. Sustituye los valores de la diagonal y el lado en la formula. Asegúrese de sustituir las variables correctas.

Por ejemplo, al determinar el ancho de un rectángulo con una diagonal de 5 cm y un lado de 4 cm, la fórmula se vería así:

5 = \sqrt{w} 2 + 4^{2}

$5={raíz cuadrada{w^{{2}}+4^{{2}}}}$

Imagen titulada Encuentra el ancho de un rectángulo Paso 11

3. Cuadrar ambos lados de la fórmula. Debe hacer esto para deshacerse del signo radical para que aislar la variable de ancho sea más fácil.

Por ejemplo:

5 = \sqrt{w} 2 + 4^{2}

$5={raíz cuadrada{w^{{2}}+4^{{2}}}}$

52 = w^{2} + 4^{2}

$5^{{2}}=w^{{2}}+4^{{2}}$

25 = w 2 + dieciséis

$25=w^{{2}}+16$

Imagen titulada Encuentra el ancho de un rectángulo Paso 12

4. Aislar la variable w{ estilo de visualización w} $w$ . Haces esto restando la longitud al cuadrado, de cada lado de la ecuación.

Por ejemplo, en la ecuación

25 = dieciséis + w 2

$25=16+w^{{2}}$ , restar 16 de cada lado.

25 = dieciséis + w 2

$25=16+w^{{2}}$

9 = w 2

$9=w^{{2}}$

Imagen titulada Encuentra el ancho de un rectángulo Paso 13

5. Resolver w{ estilo de visualización w} $w$ . Lo haces determinando la raíz cuadrada para cada lado de la ecuación.

Por ejemplo:

\sqrt{9} = \sqrt{w} 2

${sqrt{9}}={sqrt{w^{{2}}}}$

3 = w

$3=w$

Imagen titulada Encuentra el ancho de un rectángulo Paso 14

6. Anota la respuesta final. No olvides mencionar la unidad de las lecturas.

Por ejemplo, para un rectángulo con una diagonal de

5 C metro

$5cm$ y un lado de

4 C metro

$4cm$ , se convierte en el ancho

3 C metro

$3cm$ .

Método 4 de 4: usar el área o el perímetro y la longitud relativa

Imagen titulada Encuentra el ancho de un rectángulo Paso 15

1. Escribe la fórmula del área o perímetro de un rectángulo. La fórmula que utilice depende de los valores de medición dados. Si se da el área, use la fórmula del área. Si se da la circunferencia, use la fórmula de la circunferencia.

Si se desconoce el área o el perímetro, o la relación entre el largo y el ancho, no puede usar este método.
La fórmula del área es $a = (yo) (w)$ $A=(l)(w)$ .
La formula de la circunferencia es $pags = 2 yo + 2 w$ $P=2l+2w$ .
Por ejemplo, quizás dado que el área de un rectángulo es de 24 cm, entonces usas la fórmula para el área de un rectángulo.

Imagen titulada Encuentra el ancho de un rectángulo Paso 16

2. Escribe la expresión que describe la relación entre el largo y el ancho. Escribe tu expresión en una comparación con

yo

$yo$ .

La relación se puede dar diciendo cuántas veces un lado es mayor que el otro, o cuántas unidades más o menos.

Por ejemplo, se puede saber que el largo es cinco centímetros más largo que el ancho. La expresión para la longitud se convierte entonces en

yo = w + 5

$l=w+5$ .

Imagen titulada Encuentra el ancho de un rectángulo Paso 17

3. Reemplace la variable yo{ estilo de visualización l} $yo$ en la fórmula del área o perímetro por la expresión de la longitud. La fórmula ahora solo escucha la variable

w

$w$ lo que significa que puedes calcular el ancho.

Por ejemplo, si sabes que el área es de 24 cm y que

yo = w + 5

$l=w+5$ , entonces la fórmula se ve así:

a = (yo) (w)

$A=(l)(w)$

24 = (w + 5) (w)

$24=(an+5)(an)$

Imagen titulada Encuentra el ancho de un rectángulo Paso 18

4. Simplifica la ecuación. La ecuación simplificada puede tomar diferentes formas, dependiendo de la relación entre el largo y el ancho, y dependiendo de si vas por el área o el perímetro. Trate de hacer una comparación con la que Ud