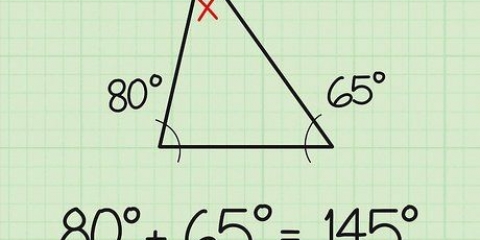
Los ángulos rectos a menudo se indican en los libros de texto y las pruebas con un pequeño cuadrado en la esquina derecha. Esta marca especial significa "90 grados." 
Si tu triángulo tiene lados de 3 y 4, y has asignado letras a esos lados para que a = 3 y b = 4, calculas la ecuación como: 3 + 4 = c. 
Si a = 3, a = 3 x 3, o 9.Si b = 4, entonces b = 4 x 4, o 16. Cuando factoriza esos valores en su ecuación, ahora debería verse así: 9 + 16 = c. 
En nuestro ejemplo, 9 + 16 = 25, toma nota entonces 25 = c. 
En nuestro ejemplo, c = 25.La raíz cuadrada de 25 es 5 (5x5 = 25, Entonces Raíz cuadrada(25) = 5).Y eso significa c = 5, la longitud de nuestra hipotenusa! 

Calcula la hipotenusa de este triángulo en función de la longitud de uno de los catetos y multiplica su longitud por Sqrt (2). Es útil saber esta razón, especialmente si tu prueba o problemas de tarea te dan las longitudes de los lados en forma de variables en lugar de números enteros. 
Dada la longitud del cateto más corto (el opuesto al ángulo de 30 grados), multiplica la longitud de ese cateto por 2 para obtener la longitud de la hipotenusa. Por ejemplo, si la longitud del cateto más corto 4 es, entonces sabes que la hipotenusa 8 debe ser. Si conoce la longitud del cateto más largo (opuesto al ángulo de 60 grados), multiplique esa longitud por2/Sqrt(3) para encontrar la longitud de la hipotenusa.Por ejemplo, si la longitud del cateto más corto 4 es, entonces sabes que la hipotenusa 4.62 debe ser. 

Para encontrar el seno de un ángulo de 80 grados, deberás pecado 80 debe escribir seguido del signo igual o Enter, o80 pecado. (La respuesta es -0.9939.) También puedes buscar "calculadora de pecado" con su navegador para algunas calculadoras fáciles de usar para que no tenga que adivinar. 
De hecho, la regla del seno se puede usar para resolver cada triángulo, pero sólo un triángulo rectángulo tendrá una hipotenusa. 

Por ejemplo, si sabes que A = 40 grados, entonces B = 180 – (90 + 40). simplificar esto a B = 180 – 130 y puedes deducir rápidamente que B = 50 grados. 
Para continuar con nuestro ejemplo, digamos que la longitud del lado a = 10.Ángulo C = 90 grados, ángulo A = 40 grados y ángulo B = 50 grados. 

A partir de nuestro ejemplo, vemos que pecado 40 = 0,64278761.Para encontrar el valor de c, dividimos la longitud de a por este número y encontramos que 10 / 0,64278761 = 15,6, la longitud de nuestra hipotenusa!
Determinar la longitud de la hipotenusa
Contenido
Todos los triángulos rectángulos tienen un ángulo recto (de 90 grados) y la hipotenusa es el lado opuesto a ese ángulo. La hipotenusa es el lado más largo del triángulo y también es muy fácil de encontrar usando varios métodos diferentes. Este artículo te enseñará cómo determinar la longitud de la hipotenusa usando el Teorema de Pitágoras, siempre que sepas la longitud de los otros dos lados del triángulo. Luego, aprenderá a calcular la hipotenusa de algunos triángulos rectángulos especiales que encontrará a menudo en las pruebas. Y finalmente aprenderás a calcular la longitud de la hipotenusa usando la regla del Seno, cuando solo se conoce la longitud de uno de los lados y la magnitud de uno de los ángulos.
Pasos
Método 1 de 3: usar el teorema de Pitágoras

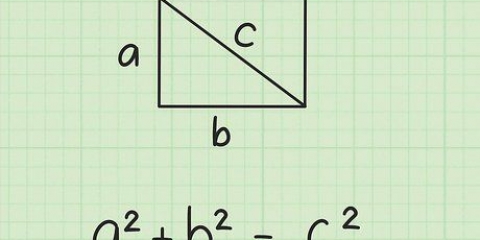
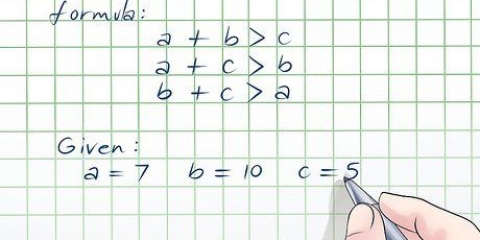
1. Aprende el teorema de Pitágoras. El Teorema de Pitágoras describe la relación entre los lados de un triángulo rectángulo. Establece que para un triángulo rectángulo arbitrario con lados a y b, e hipotenusa de longitud c, tenemos a + b = c.

2. Asegúrate de que tu triángulo sea un triángulo rectángulo.El teorema de Pitágoras solo funciona para triángulos rectángulos y, por definición, solo un triángulo rectángulo puede tener una hipotenusa.Si tu triángulo contiene un ángulo de exactamente 90 grados, entonces es un triángulo rectángulo y puedes continuar.

3. Asigna las variables a, b y c a los lados de tu triángulo.La variable "C" siempre se asigna a la hipotenusa, es decir, el lado más largo.Elija uno de los otros lados para el a, y nombra el lado restante B (no importa cuál, las matemáticas siguen siendo las mismas).Luego procesa las longitudes de a y b en la fórmula, como se muestra en el siguiente ejemplo:

4. Determinar los cuadrados de a y b.Para encontrar el cuadrado de un número, simplemente multiplique ese número por sí mismo, entonces un = un x un. Encuentre los cuadrados de a y b e incorpórelos a la fórmula.

5. Contar los valores dea y B juntos en. Factoriza esto en tu ecuación, y te da el valor de c. Ahora solo falta un paso y has determinado la hipotenusa!

6. Determinar la raíz cuadrada de c. Usa la función de raíz cuadrada en tu calculadora (o las tablas de multiplicar, si las sabes de memoria) para encontrar la raíz cuadrada de c. La respuesta es la longitud de tu hipotenusa!
Método 2 de 3: Determinar la hipotenusa de triángulos rectángulos especiales

1. Aprende a reconocer los triángulos de un trío pitagórico. Las longitudes de los lados de una tríada de Pitágoras son números enteros que obedecen al Teorema de Pitágoras. Encontrará regularmente estos triángulos especiales en los libros de texto de geometría y en las pruebas estándar como el SAT y el GRE.En particular, si memorizas las primeras 2 ternas pitagóricas, puedes ahorrarte mucho tiempo en esas pruebas porque inmediatamente sabes la hipotenusa de cualquiera de estos triángulos con solo mirar las longitudes de los lados!
- El primer trío pitagórico es 3-4-5 (3 + 4 = 5, 9 + 16 = 25).Cuando ves un triángulo rectángulo con lados de longitud 3 y 4, inmediatamente sabes con certeza que la hipotenusa será 5 sin tener que hacer ningún cálculo.
- La razón de un triple pitagórico sigue siendo la misma incluso cuando los lados se multiplican por un número diferente. Por ejemplo: un triángulo rectángulo con lados 6 y 8 tendrá una hipotenusa de 10 (6 + 8 = 10, 36 + 64 = 100).Lo mismo se aplica a9-12-15, incluso 1.5-2-2.5.Haz los cálculos y verás!
- El segundo trío pitagórico que encontrarás a menudo en las pruebas es 5-12-13 (5 + 12 = 13, 25 + 144 = 169).También tenga cuidado con sus plurales, como 24-10-26 y 2.5-6-6.5.

2. Aprende la razón de los lados de un triángulo rectángulo con ángulos 45-45-90. Un triángulo rectángulo de 45-45-90 tiene ángulos de 45, 45 y 90 grados, y también se llama triángulo rectángulo isósceles. Este se encuentra con frecuencia en las pruebas estándar y es un triángulo muy fácil de resolver. La razón de los lados de este triángulo es 1:1:Raíz cuadrada(2), lo que significa que la longitud de los catetos es igual, y la longitud de la hipotenusa es simplemente la longitud de los catetos multiplicada por la raíz cuadrada de dos.

3. Aprende las proporciones de un triángulo de ángulo recto 30-60-90. Este triángulo tiene ángulos de 30, 60 y 90 grados y se puede formar dividiendo un triángulo equilátero por la mitad. Los lados del triángulo rectángulo 30-60-90 siempre tienen la razón 1:Raíz cuadrada(3):2, o x:Raíz cuadrada(3)x:2x.Si se le da la longitud de un cateto del triángulo rectángulo 30-60-90 y se le pide que determine la hipotenusa, es muy fácil de hacer:
Método 3 de 3: calcular la hipotenusa con la regla del seno

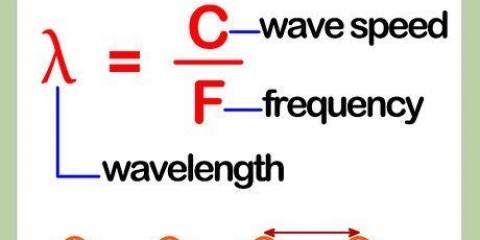
1. Entender lo que el "Seno" medio. Los términos "seno," "coseno" y "tangente" todos se refieren a ciertas relaciones entre los ángulos y/o los lados de un triángulo rectángulo.En un triángulo rectángulo, el es seno de un ángulo definido como la longitud del lado opuesto al ángulo dividido por la hipotenusa del triangulo. La abreviatura de seno tal como aparece en su calculadora es pecado.

2. Aprende a calcular el seno. Incluso una simple calculadora científica tiene una función seno. Mira la llave marcada pecado.Para encontrar el seno de un ángulo, generalmente presionará la tecla pecado-y luego ingrese el ángulo en grados.Sin embargo, en algunas calculadoras primero debe ingresar el ángulo en grados y luego presionar la tecla pecado-presiona el botón. Tendrás que experimentar con tu calculadora o buscar en el manual para determinar cuál es.

3. Aprende la regla del seno.La regla del seno es una herramienta útil para resolver problemas de triángulos. Puede usarlo principalmente para encontrar la hipotenusa de un triángulo rectángulo, si conoce la longitud de un lado y uno de sus ángulos que no sea el ángulo recto. Para cualquier triángulo con lados a, B y C y las esquinas a, B y C, la regla del seno establece que a / pecado a = B / pecado B = C / pecado C.

4. Asigna las variables a, b y c a los lados de tu triángulo. La hipotenusa (el lado más largo) siempre debe ser el "C" son. Para simplificar, etiquete el lado de longitud conocida como "a" y otros "B". Luego asigna las variables A, B y C a las esquinas del triángulo. El ángulo recto opuesto a la hipotenusa se convierte en "C".la esquina de enfrente "a" es ángulo "a" y el ángulo del lado opuesto "B" es "B".

5. Calcular el tercer ángulo. Porque es un ángulo recto eso ya lo sabes C = 90 grados y también sabes qué ángulo a o B es. Dado que la suma de todos los ángulos en un triángulo siempre debe ser igual a 180 grados, es fácil calcular el tercer ángulo usando la fórmula: 180 – (90 + A) = B. También puedes invertir esta ecuación para que 180 – (90 + B) = A.

6. Examina tu triángulo.En este punto conoces todos los ángulos del triángulo y la longitud del lado a. Ahora es el momento de procesar estos valores en la regla del seno, para calcular la longitud de los otros dos lados.

7. Aplica la regla del seno a tu triángulo.Solo necesitamos procesar nuestros números y resolver la siguiente ecuación, para encontrar la longitud de la hipotenusa c: longitud del lado a/ pecado A = longitud del lado c/ pecado C.Esto todavía puede parecer un poco intimidante, pero el seno de 90 grados es una constante y siempre es igual a 1!Por lo tanto, nuestra ecuación se puede simplificar a: a / pecado A = c / 1, o más simple a / pecado una = c.

8. Divide la longitud de la sedaa a través del seno del ángulo a para encontrar la longitud de la hipotenusa!Puede calcular esto en dos pasos separados, primero: pecado Calcula y escribe A, luego divide por a. O pruébalo todo a la vez en tu calculadora. Si haces esto, no olvides los paréntesis después del signo de división.Por ejemplo, introduzca 10 / (pecado 40) o 10 / (40 pecado), dependiendo de tu calculadora.
Artículos sobre el tema. "Determinar la longitud de la hipotenusa"
Оцените, пожалуйста статью
Similar
Popular